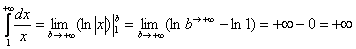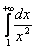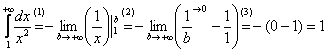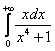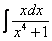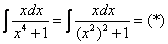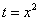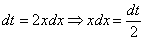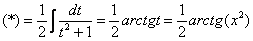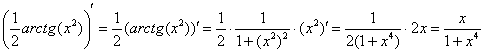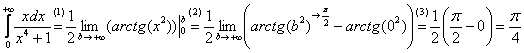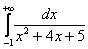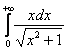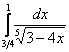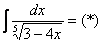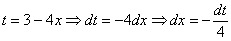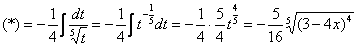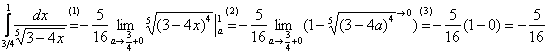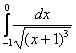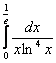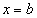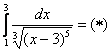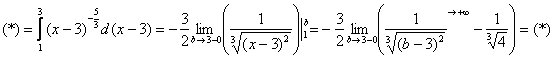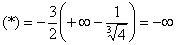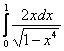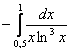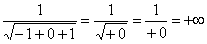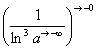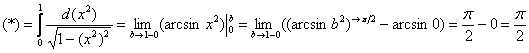сходимость несобственного интеграла с параметром
Равномерная сходимость несобственных интегралов, зависящих от параметра
Считаем, что f непрерывна в этой полосе.
Признак Вейерштрасса равномерной сходимости несобственных интегралов [ править ]
| Теорема (Вейерштрасс, Признак равномерной сходимости несобственных интегралов): |
| Доказательство: |
| [math]\triangleright[/math] |
| $ B > A: \left |
| [math]\triangleleft[/math] |
Свойства несобственных интегралов, зависящих от параметра [ править ]
Непрерывность [ править ]
Доказательство ведем по аналогии с рядами.
В силу равномерной сходимости:
$ \forall \varepsilon > 0: \exists A_0: \forall A \ge A_0: \left| \int\limits_A^ <\infty>f(x, y) dx \right| 0: | \Delta y | Повторное интегрирование. [ править ]
Надо установить формулу:
В силу предыдущего параграфа:
Отметим, что интегралы существуют по пункту 1 (непрерывность F по y).
По определению несобственного интеграла, формула верна.
Замечание: можно поставить вопрос:
В ряде частных случаев, ответ будет положительным.
В теории интеграла Лебега будет доказана знаменитая теорема Фубини, полностью решающая этот вопрос, но уже на языке интеграла Лебега.
Формула Лейбница [ править ]
Доказываем по аналогии с функциональными рядами.
Значит, ее можно интегрировать.
По предыдущему пункту, меняем порядок интегрирования.
Бета- и Гамма-функции Эйлера [ править ]
В обоих случаях: интегралы, зависящие от параметра.
Гамма-функция [ править ]
Эта задача решается Гамма-функцией.
Требуется проверить равномерную сходимость интеграла от частной производной.
Аналогично, при двойном дифференцировании получаются равномерно сходящиеся интегралы и т.д.
Можно писать аналогичные формулы, приведенные для Бета-функции, а также связь бета- и гамма-функции с помощью формулы Эйлера:
Несобственные интегралы, зависящие от параметра. Равномерная сходимость
Равномерная сходимость несобственных интегралов по параметру.
Предположим, что выполнены следующие условия:
Интеграл
$$
\int\limits_<0>^ <+\infty>e^ <-x>\cos xy\ dx\label
$$
сходится равномерно по параметру у на интервале \((-\infty, +\infty) = \mathbb
\(\vartriangle\) Для любого \(\varepsilon > 0\) существует \(b’ = \displaystyle\ln \frac<2><\varepsilon>\) такое, что для любого \(\xi \in [b’, +\infty)\) и любого \(y \in Y\) выполняется неравенство
$$
\left|\int\limits_<\xi>^ <+\infty>e^ <-x>\cos xy\ dx\right| \leq \int\limits_<\xi>^ <+\infty>e^<-x>\ dx = e^ <-\xi>\leq e^ <-b’>= \frac<\varepsilon> <2>Определение.
Интеграл
$$
I_
$$
сходится неравномерно по параметру \(y\) на полуинтервале \([0, +\infty)\).
\(\vartriangle\) Возьмем \(\varepsilon = e^<-1>\). Тогда для любого \(b’ \in (0, +\infty)\) существует \(\xi = b’\) и \(y = 1/b’\) такие, что
$$
\int\limits_<\xi>^ <+\infty>ye^<-xy>\ dx = \int\limits_
$$
и поэтому интеграл \(\displaystyle I_
Признаки равномерной сходимости несобственных интегралов по параметру.
(Признак Вейерштрасса равномерной сходимости несобственного интеграла по параметру).
Пусть для любого \(y \in Y\) функция \(f(x, y)\) интегрируема по \(x\) на любом отрезке \([a, b’] \subset [a, b)\), и пусть на \([a, b)\) существует функция \(\varphi(x)\) такая, что для всех \(y \in Y\) и всех \(x \in [a, b)\) выполнено неравенство \(|f(x, y)| \leq \varphi(x)\), а несобственный интеграл \(\displaystyle\int\limits_^ \varphi(x)\ dx\) сходится.
Интеграл
$$
\int\limits_<0>^ <+\infty>\frac<\cos xy><1+x^<2>>\ dx\label
$$
сходится равномерно по параметру \(y\) на интервале \((-\infty, +\infty)\).
\(\vartriangle\) Так как \(\displaystyle\frac<|\cos xy|><1+x^<2>> \leq \frac<1><1+x^<2>>\) и \(\displaystyle\int\limits_<0>^ <+\infty>\frac
Докажем признак Дирихле равномерной сходимости для интегралов вида
$$
\int\limits_^ <+\infty>f(x, y) g(x, y)\ dx,\ y \in Y.\label
$$
(Признак Дирихле равномерной сходимости несобственного интеграла по параметру).
Тогда интеграл \eqref
\(\circ\) По признаку Дирихле несобственный интеграл \eqref
Так как по условию 4) функция \(\psi(x) \rightarrow 0\) при \(x \rightarrow +\infty\), то для любого \(\varepsilon > 0\) существует \(a’ > a\) такое, что для любого \(\xi \in [a’, +\infty)\) выполнено неравенство
$$
\psi(\xi) Замечание 2.
Если \(+\infty\) — единственная особая точка сходящегося интеграла \eqref
Поэтому для справедливости утверждения теоремы 2 достаточно, чтобы условия 1)-4) выполнялись на некотором промежутке \([a’, +\infty) \subset [a, +\infty)\).
Интеграл
$$
\int\limits_<0>^ <+\infty>e^ <-xy>\frac<\sin x>
$$
сходится равномерно по параметру \(y\) при \(y \in [0, +\infty)\).
\(\vartriangle\) Так как функция \(\sin x\) имеет ограниченную первообразную, а при \(x \geq 1\), \(y \geq 0\) выполнены следующие условия:
$$
\frac<\partial> <\partial x>\left(\frac
(Критерий Коши равномерной сходимости несобственного интеграла по параметру).
Получаем, что для любого \(\xi \in [b’, b)\) и для любого \(y \in Y\) выполнено неравенство \(\displaystyle\left|\int\limits_<\xi>^ f(x, y)\ dx\right| \leq \varepsilon\), из которого следует, что интеграл \(\int\limits_^ f(x, y)\ dx\) сходится равномерно по параметру \(y\) на множестве \(Y\). \(\bullet\)
Применяя правило построения отрицания, получаем из критерия Коши полезное следствие.
Если существует \(\varepsilon_ <0>> 0\) такое, что для любого \(b’ \in [a, b)\) существуют \(\xi_<0>, \xi’_ <0>\in [b’, b)\) и существует \(y_ <0>\in Y\) такие, что
$$
\left|\int\limits_<\xi_<0>>^<\xi’_<0>> f(x, y_<0>)\ dx\right| \geq \varepsilon_<0>,
$$
то интеграл \(\displaystyle\int\limits_^ f(x, y)\ dx\) не сходится равномерно по параметру \(y\) на множестве \(Y\).
Интеграл
$$
\int\limits_<0>^ <+\infty>e^<-\alpha x^<2>>\ dx\label
$$
сходится равномерно по параметру \(\alpha\) на множестве \([\alpha_<0>, +\infty)\), \(\alpha_ <0>> 0\), и сходится неравномерно на множестве \((0, +\infty)\).
\(\vartriangle\) Пусть \(\alpha \geq \alpha_ <0>> 0\). Так как \(e^<-\alpha x^<2>> \leq e^ <-\alpha_<0>x^<2>>\) и \(\displaystyle\int\limits_<0>^ <+\infty>e^<-\alpha x^<2>>\ dx\) сходится, то по признаку Вейерштрасса интеграл \eqref
Пусть теперь \(\alpha \in (0, +\infty)\). Покажем, что на \((0, +\infty)\) интеграл \eqref
$$
\int\limits_<\xi_<0>>^<\xi’_<0>> e^ <-\alpha_<0>x^<2>>\ dx = \int\limits_^
$$
и, следовательно, интеграл \eqref
Непрерывность, интегрируемость и дифференцируемость несобственного интеграла по параметру.
\(\vartriangle\) Если функцию \(\displaystyle\frac<\sin x>
При рассмотрении примера 4 было показано, что интеграл \eqref
(Теорема о перестановке порядка интегрирования).
\(\vartriangle\) Воспользуемся известной формулой
$$
\int\limits_<0>^ <+\infty>e^ <-xy>\sin x\ dx = \frac<1><1+y^<2>>,\ y > 0.\label
$$
Интеграл \eqref
$$
|e^ <-xy>\sin x\ dx| \leq e^<-\delta x>,\quad \int\limits_<0>^ <+\infty>e^<-\delta x>\ dx = \frac<1><\delta>.\nonumber
$$
Применяя теорему 5 и интегрируя равенство \eqref
$$
\operatorname
$$
Так как \(|\sin x| \leq x\) при \(x \geq 0\), то
$$
\left|\int\limits_<0>^ <+\infty>\dfrac
$$
Переходя к пределу при \(N \rightarrow +\infty\) в равенстве \eqref
$$
\frac<\pi><2>-\operatorname
$$
Воспользовавшись равенством \eqref
(Теорема о дифференцировании несобственного интеграла по параметру).
Пусть функции \(f(x, y)\) и \(f_
\(\circ\) Пусть \(c \leq y \leq d\). Рассмотрим интеграл \(\displaystyle\int\limits_^ f_
Покажем, что \(C_ <2>= 0\). Так как
$$
|I_<1>(y)| = \left|\int\limits_<0>^ <+\infty>\frac<\cos xy><1+x^<2>>\ dx\right| \leq \int\limits_<0>^ <+\infty>\frac<|\cos xy|><1+x^<2>>\ dx \leq \int\limits_<0>^ <+\infty>\frac
$$
то \(I_<1>(y)\) есть ограниченная функция на \([\delta, +\infty)\). Так как \(e^
Замечая, что интеграл Лапласа \(I_<1>(y)\) есть четная функция на \((-\infty, +\infty)\), а интеграл \(I_<2>(y)\) есть нечетная функция на \((-\infty, +\infty)\), перепишем равенство \eqref
$$
I_<1>(y) = C_<1>e^<-|y|>,\ I_<2>(y) = C_<1>\ \operatorname
$$
Для определения произвольной постоянной \(C_<1>\) воспользуемся тем, что интеграл Лапласа \(I_<1>(y)\) сходится равномерно по параметру \(y\) на \((-\infty, +\infty)\) (пример 3). Поэтому \(I_<1>(y)\) есть непрерывная функция в точке \(y = 0\). Следовательно,
$$
\frac<\pi> <2>= \int\limits_<0>^ <+\infty>\frac
$$
Теперь формулы \eqref
$$
\int\limits_<0>^ <+\infty>\frac<\cos xy><1+x^<2>>\ dx = \frac<\pi><2>e^<-|y|>,\\ \int\limits_<0>^ <+\infty>\frac
$$
То, что формулы \eqref
Перестановка порядка интегрирования в том случае, когда оба интеграла несобственные.
В теореме 5 была обоснована перестановка порядка интегрирования, когда внутренний интеграл несобственный, а внешний собственный. Сложнее обосновывать перестановку порядка интегрирования, когда оба интеграла несобственные.
Пусть функция \(f(x, y)\) непрерывна на множестве \(\<(x, y): a \leq x \leq b,\ c \leq y \leq d\>\) и выполнены следующие условия:
Теоремы 4-7 остаются справедливыми и при замене функции \(f(x, y)\) на функцию \(\psi(x)f(x, y)\), где функция \(\psi(x)\) интегрируема по Риману на любом отрезке, лежащем в интервале \((a, b)\).
Если \(f(x, y) = \varphi(x, y)+i\psi(x, y)\) есть комплекснозначная функция, то
$$
|\varphi(x, y)| \leq |f(x, y)|,\ |\psi(x, y)| \leq |f(x, y)|.\nonumber
$$
Все условия теоремы будут выполнены и для функций \(\varphi(x, y)\) и \(\psi(x, y)\), если \(f(x, y)\) удовлетворяет условиям теоремы 7. Поэтому оба повторных интеграла от каждой из этих функций существуют и равны. Следовательно, существуют и равны повторные интегралы от функции \(f(x, y)\).
Вычислить интеграл Эйлера-Пуассона (интеграл вероятностей)
$$
I = \int\limits_<0>^ <+\infty>e^<-t^<2>> dt.\nonumber
$$
Для обоснования законности изменения порядка интегрирования применим теорему 7. Интеграл \(\displaystyle\int\limits_<0>^ <+\infty>ye^<-y^<2>(1+x^<2>)> dx\) сходится равномерно по параметру \(y\) на любом отрезке \([c, d] \subset (0, +\infty)\) по признаку Вейерштрасса, так как \(|ye^<-y^<2>(1+x^<2>)>| \leq de^<-c^<2>(1+x^<2>)>\) а интеграл \(\displaystyle\int\limits_<0>^ <+\infty>de^<-c^<2>(1+x^<2>)> dx\) сходится.
Аналогично доказывается, что интеграл \(\displaystyle\int\limits_<0>^ <+\infty>ye^<-y^<2>(1+x^<2>)> dx\) сходится равномерно по параметру \(x\) на любом отрезке \([a, b] \subset (0, +\infty)\). Повторный интеграл \(\int\limits_<0>^ <+\infty>ye^<-y^<2>(1+x^<2>)> dx\) сходится в силу равенства \eqref
Вычислить интегралы Френеля
$$
J_ <1>= \int\limits_<0>^ <+\infty>\sin x^<2>\ dx,\ J_ <2>= \int\limits_<0>^ <+\infty>\cos x^<2>\ dx.
$$
При написании формул \eqref
Изменение порядка интегрирования при \(k > 0\) обосновывается при помощи теоремы 7, предельный переход при \(k \rightarrow +0\) под знаком интеграла возможен в силу его равномерной сходимости по параметру \(k\) при \(k \in [0, +\infty)\) (признак Вейерштрасса). Интегралы \(\displaystyle\int\limits_<0>^ <+\infty>\frac
Интегралы, зависящие от параметра
Содержание:
По этой ссылке вы найдёте полный курс лекций по математике:
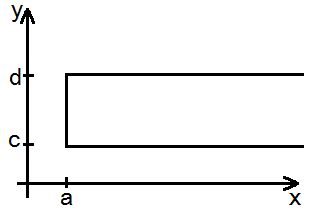
Собственные интегралы, зависящие от параметра 1.1. Понятие интеграла, зависящего от параметра, и его непрерывность Пусть в прямоугольнике определена функция двух переменных f(x, у) (рис. 1). Предположим, что при любом фиксированном значении у е [с, d] существует интеграл ь Ясно, что этот интеграл является функцией переменного у, Интеграл (1) называется интегралом, зависящим от параметра у. Имеет место следующая теорема о непрерывности интеграла, зависящего от параметра.
Теорема 1:
Если функция /(х, у) непрерывна в прямоугольнике П, то функция /(у), определенная соотношением (1), непрерывна на отрезке [с, d\. Из формулы (1) вытекает, что приращение ) функции /(у), соответствующее приращению аргумента Ду, можно оценить так: По условию теоремы функция f
Возможно вам будут полезны данные страницы:
Интеграл (1) называется абсолютно сходящимся на отрезке [с, d\, если сходится интеграл Собственные интегралы зависящие от параметра Дифференцирование интеграла no параметру Интегрирование интеграла по параметру Понятие несобственного интеграла первого рода, зависящего от параметра Равномерная сходимость несобственного интеграла Критерий Коши Свойства равномерно сходящихся несобственных интегралов, зависящих от параметра 2.2. Равномерная сходимость несобственного интеграла. Критерий Коши Определение 2.
Несобственный интеграл
Несобственный интеграл (1) называется равномерно сходящимся по параметру у наотрезке [с, d), если он сходится наэтомотрезкеи для любого е > 0 можно указать такое А ^ а, зависящее только от е, что для всех В > А и для всех у из отрезка [с, d\ выполняется неравенство Имеетместоследующий критерий Коши равномерной сходимости несобстве нных интегралов, зависящих от параметра.
Теорема 4. Для того, чтобы несобственный интеграл (1) равномерно сходился по параметру у на отрезке [с, d\, необходимо и достаточно, чтобы для любого е > 0 можно было указать число А ^ а, зависящее только от е и такое, что для любых В и С, больших А, и для всех у из отрезка [с, d] выполнялось неравенство Справедливость этого критерия вытекает непосредственно из определения равномерной сходимости. Сформулируем достаточный признак равномерной сходимости несобственных интегралов, зависящих от параметра. Теорема 5 (признак Вейерштрасса).
Пусть функция /(х, у) определена в пыупыосе Поо и для каждого у € | с, d] интегрируема по х на любом отрезке [а, Л]. Пусть, кроме того, для всех точек полуполосы П^ выполняется неравенство Тогда из сходимости интеграла f g(x) dx вытекает равномерная сходимость по у наот- резке [с, d] несобственного интегрша В силу критерия Коши сходимости интеграла от функции для любого е > О можно указать число А ^ а такое, что при всех С > В ^ А выполняется неравенство Используя неравенство (4), отсюда получим, что для всех у из отрезка Тем самым, критерий Коши равномерной сходимости интеграла выполнен. Цитр 1.
Иссладова тъ на равномерную сходимость несобственный иктграл где я — параметр, Так как при любом произвольные вещественные числа, выполняется неравенство и интеграл сходится, то по признаку Вейерштрасса интеграл (5) равномерно сходится для всех 2.3. Свойства равномерно сходящихся несобственных интегралов, зависящих от параметра Свойство 1. Непрерывность несобственного интеграла по параметру. Если функция непрерывна в области Поо и интеграл сходится равномернопо у наотрезкс (с, dj,то функция 1(у) непрерывна на Свойство 2. Интегрируемость несобственно го интеграла по параметру.
В самом деле, при любом в, и откуда по признаку Вейерштрасса следует равномерная сходимость интеграла (9). Обозначая подынтегральную функцию интеграла (5) через замечаем, что — подынтегральная функция равномерно сходящегося интеграла (9). Используя свойство дифференцируемое™ несобственного интеграла по параметру, получим Так как 1($) = (в этом легко убедиться путем интегрирования по частям), то Отсюда Пример 3.
Покажем сначала, что несобственный интеграл Собственные интегралы зависящие от параметра Дифференцирование интеграла no параметру Интегрирование интеграла по параметру Понятие несобственного интеграла первого рода, зависящего от параметра Равномерная сходимость несобственного интеграла Критерий Коши Свойства равномерно сходящихся несобственных интегралов, зависящих от параметра зависящий от параметра у, сходится равномерно на отрезке (а, 6).
Присылайте задания в любое время дня и ночи в ➔ 
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Несобственные интегралы. Примеры решений
К изучению несобственных интегралов лучше приступать в последнюю очередь в ходе изучения интегрального исчисления функции одной переменной. Читатель данного урока должен быть хорошо подкован в неопределенных интегралах, определенных интегралах, уметь находить площадь плоской фигуры с помощью определенного интеграла. Кроме того, потребуются знания простейших пределов и графиков элементарных функций. По логике изложения материала эта статья является продолжением урока Определенный интеграл. Как вычислить площадь фигуры.
Вы еще здесь? =) Нет, я никого не пытался запугать, просто тема несобственных интегралов – очень хорошая иллюстрация тому, как важно не запускать высшую математику и другие точные науки. Для освоения урока на сайте всё есть – в подробной и доступной форме, было бы желание….
Итак, начнем-с. Образно говоря, несобственный интеграл – это «продвинутый» определенный интеграл, и на самом деле сложностей с ними не так уж и много, к тому же у несобственного интеграла есть очень хороший геометрический смысл.
Что значит вычислить несобственный интеграл?
Вычислить несобственный интеграл – это значит, найти ЧИСЛО (точно так же, как в определенном интеграле), или доказать, что он расходится (то есть, получить в итоге бесконечность вместо числа).
Несобственные интегралы бывают двух видов.
Несобственный интеграл с бесконечным пределом (ами) интегрирования
Иногда такой несобственный интеграл называют несобственным интегралом первого рода. В общем виде несобственный интеграл с бесконечным пределом чаще всего выглядит так: 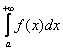
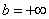
Реже встречаются интегралы с бесконечным нижним пределом 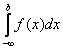
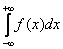
Ну а сейчас разберём самый популярный случай 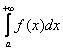
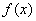
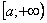
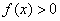
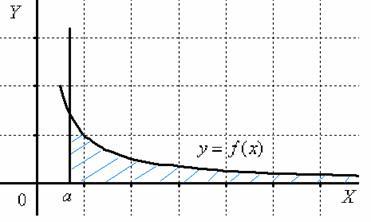
Обратите внимание, что она бесконечна (не ограничена справа), и несобственный интеграл 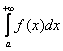
1) Первая мысль, которая приходит в голову: «раз фигура бесконечная, то 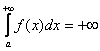
2) Но. Как это ни парадоксально прозвучит, площадь бесконечной фигуры может равняться… конечному числу! Например: 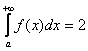
3) О третьем варианте чуть позже.
В каких случаях несобственный интеграл расходится, а в каком сходится? Это зависит от подынтегральной функции 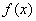
А что будет, если бесконечная криволинейная трапеция расположена ниже оси? В этом случае, несобственный интеграл 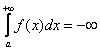
Таким образом, несобственный интеграл может быть отрицательным.
Важно! Когда Вам для решения предложен ЛЮБОЙ несобственный интеграл, то, вообще говоря, ни о какой площади речи не идет и чертежа строить не нужно. Геометрический смысл несобственного интеграла я рассказал только для того, чтобы легче было понять материал.
Коль скоро несобственный интеграл очень похож на определенный интеграл, то вспомним формулу Ньютона- Лейбница: 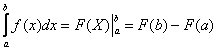
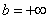
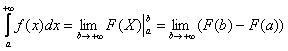
В чем отличие от определенного интеграла? Да ни в чем особенном! Как и в определенном интеграле, нужно уметь находить первообразную функцию 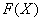
Рассмотрим два классических примера:
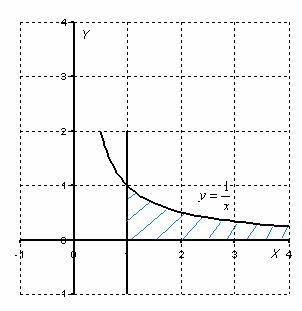
Вычислить несобственный интеграл или установить его расходимость.
Для наглядности я построю чертеж, хотя, еще раз подчеркиваю, на практике строить чертежи в данном задании не нужно.
Подынтегральная функция 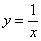
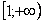
Применение нашей формулы 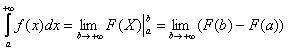
То есть, несобственный интеграл расходится, и площадь заштрихованной криволинейной трапеции равна бесконечности.
В рассмотренном примере у нас простейший табличный интеграл и такая же техника применения формулы Ньютона-Лейбница, как в определенном интеграле. Но применяется эта формула под знаком предела. Вместо привычной буквы 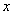
Если Вам не понятно почему 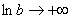
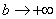
При решении несобственных интегралов очень важно знать, как выглядят графики основных элементарных функций!
Чистовое оформление задания должно выглядеть примерно так:
“ 
Подынтегральная функция непрерывна на 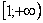
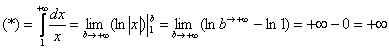
Несобственный интеграл расходится.
“
! При оформлении примера всегда прерываем решение, и указываем, что происходит с подынтегральной функцией – непрерывна она на промежутке интегрирования или нет. Этим мы идентифицируем тип несобственного интеграла и обосновываем дальнейшие действия.
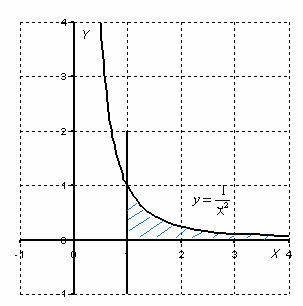
Вычислить несобственный интеграл или установить его расходимость.
Выполним чертеж:
Во-первых, замечаем следующее: подынтегральная функция 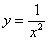
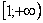
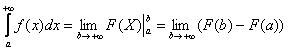
(1) Берем простейший интеграл от степенной функции (этот частный случай есть во многих таблицах). Минус лучше сразу вынести за знак предела, чтобы он не путался под ногами в дальнейших вычислениях.
(2) Подставляем верхний и нижний пределы по формуле Ньютона-Лейбница.
(3) Указываем, что 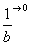
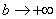
Вот здесь площадь бесконечной криволинейной трапеции равна конечному числу! Невероятно, но факт.
Чистовое оформление примера должно выглядеть примерно так:
“ 
Подынтегральная функция непрерывна на 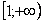
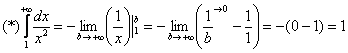
“
Что делать, если вам встретится интеграл наподобие 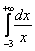
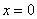
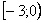
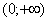
Иногда вследствие опечатки либо умысла несобственного интеграла может вовсе не существовать, так, например, если в знаменатель вышеуказанного интеграла поставить квадратный корень из «икс», то часть промежутка интегрирования вообще не войдёт в область определения подынтегральной функции.
Более того, несобственного интеграла может не существовать даже при всём «видимом благополучии». Классический пример: 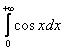
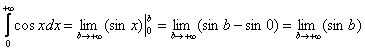
И такие примеры пусть редко, но встречаются на практике! Таким образом, помимо сходимости и расходимости, есть ещё и третий исход решения с полноправным ответом: «несобственного интеграла не существует».
Следует также отметить, что строгое определение несобственного интеграла даётся именно через предел, и желающие могут ознакомиться с ним в учебной литературе. Ну а мы продолжаем практическое занятие и переходим к более содержательным задачам:
Вычислить несобственный интеграл или установить его расходимость.
Подынтегральная функция непрерывна на 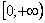
Интеграл не так прост, особенно для чайника. Что делать, если интеграл кажется не самым простым или не сразу понятно как его решать? В этом случае целесообразно применить алгоритм, о котором я уже рассказал в статье Определенный интеграл. Примеры решений.
Сначала попытаемся найти первообразную функцию 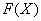
На какой из табличных интегралов похожа подынтегральная функция? Напоминает она арктангенс: 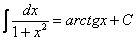
Проведем замену:
Неопределенный интеграл найден, константу 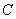
На черновике всегда полезно выполнить проверку, то есть продифференцировать полученный результат:
Получена исходная подынтегральная функция, значит, неопределенный интеграл найден правильно.
Теперь находим несобственный интеграл:
(1) Записываем решение в соответствии с формулой 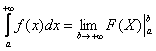
(2) Подставляем верхний и нижний пределы в соответствии с формулой Ньютона-Лейбница. Почему 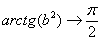
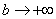
(3) Получаем окончательный ответ. Тот факт, что 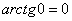
Продвинутые студенты могут не находить отдельно неопределенный интеграл, и не использовать метод замены, а использовать метод подведения функции под знак дифференциала и решать несобственный интеграл «сразу». В этом случае решение должно выглядеть примерно так:
“ 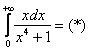
Подынтегральная функция непрерывна на 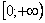
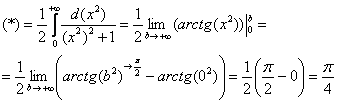
“
А сейчас два примера для самостоятельного решения.
Вычислить несобственный интеграл или установить его расходимость.
! Это типовой пример, и похожие интегралы встречаются очень часто. Хорошо его проработайте! Первообразная функция здесь находится методом выделения полного квадрата, более подробно с методом можно ознакомиться на уроке Интегрирование некоторых дробей.
Вычислить несобственный интеграл или установить его расходимость.
Этот интеграл можно решить подробно, то есть сначала найти неопределенный интеграл, проведя замену переменной. А можно решить «сразу» – подведением функции под знак дифференциала. У кого какая математическая подготовка.
Полные решения и ответы в конце урока.
Примеры решений несобственных интегралов с бесконечным нижним пределом интегрирования можно посмотреть на странице Эффективные методы решения несобственных интегралов. Там же разобран случай, когда оба предела интегрирования бесконечны.
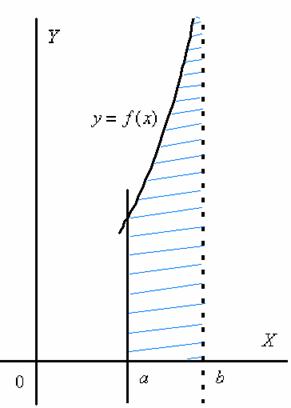
Несобственные интегралы от неограниченных функций
Или несобственные интегралами второго рода. Несобственные интегралы второго рода коварно «шифруются» под обычный определенный интеграл и выглядят точно так же: 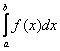
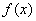
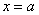
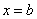
Если подынтегральной функции не существует в точке
Сразу пример, чтобы было понятно: 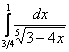
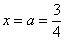
Вообще при анализе несобственного интеграла всегда нужно подставлять в подынтегральную функцию оба предела интегрирования. В этой связи проверим и верхний предел: 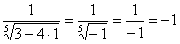
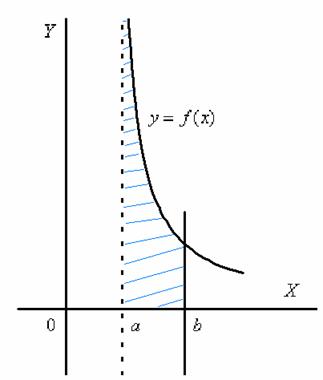
Криволинейная трапеция для рассматриваемой разновидности несобственного интеграла принципиально выглядит так:
Здесь почти всё так же, как в интеграле первого рода.
Наш интеграл численно равен площади заштрихованной криволинейной трапеции, которая не ограничена сверху. При этом могут быть два варианта*: несобственный интеграл расходится (площадь бесконечна) либо несобственный интеграл равен конечному числу (то есть, площадь бесконечной фигуры – конечна!).
* по умолчанию привычно полагаем, что несобственный интеграл существует
Осталось только модифицировать формулу Ньютона-Лейбница. Она тоже модифицируется с помощью предела, но предел стремится уже не к бесконечности, а к значению 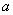
Посмотрим, как это реализуется на практике.
Вычислить несобственный интеграл или установить его расходимость.
Подынтегральная функция терпит бесконечный разрыв в точке 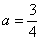
Сначала вычислим неопределенный интеграл:
Замена:
У кого возникли трудности с заменой, обратитесь к уроку Метод замены в неопределенном интеграле.
Вычислим несобственный интеграл:
(1) Что здесь нового? По технике решения практически ничего. Единственное, что поменялось, это запись под значком предела: 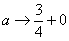
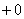
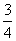
(2) Подставляем верхний и нижний предел по формуле Ньютона Лейбница.
(3) Разбираемся с 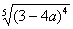
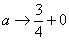
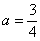
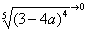
В данном случае несобственный интеграл равен отрицательному числу. В этом никакого криминала нет, просто соответствующая криволинейная трапеция расположена под осью 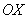
А сейчас два примера для самостоятельного решения.
Вычислить несобственный интеграл или установить его расходимость.
Вычислить несобственный интеграл или установить его расходимость.
Если подынтегральной функции не существует в точке
Бесконечная криволинейная трапеция для такого несобственного интеграла принципиально выглядит следующим образом:
Здесь всё абсолютно так же, за исключением того, что предел у нас стремится к значению 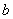
Вычислить несобственный интеграл или установить его расходимость.
Подынтегральная функция терпит бесконечный разрыв в точке 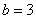
Для разнообразия я решу этот интеграл сразу – методом подведения функции под знак дифференциала. Те, кому трудно, могут сначала найти неопределенный интеграл по уже рассмотренной схеме.
Добавка 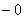
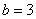
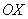
Разбираемся, почему дробь 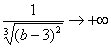
Подставляем под корень предельное значение 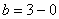
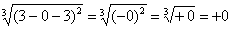
Окончательно:
Несобственный интеграл расходится.
Будьте очень внимательны в знаках. Да, конечно, несобственный интеграл расходится, но 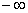
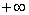
И заключительные два примера для самостоятельного рассмотрения:
Вычислить несобственный интеграл или установить его расходимость.
Вычислить несобственный интеграл или установить его расходимость.
Разбор ситуации, когда оба предела интегрирования «плохие», или точка разрыва содержится прямо на отрезке интегрирования, можно найти в статье Эффективные методы решения несобственных интегралов.
Пример 4: Решение:
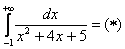
Подынтегральная функция непрерывна на 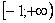

Пример 5: Решение: 
Подынтегральная функция непрерывна на 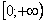
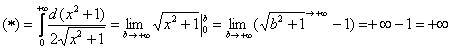
Несобственный интеграл расходится.
Пример 7: Решение: 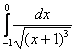
Подынтегральная функция терпит бесконечный разрыв в точке 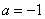
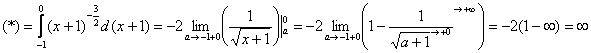
Несобственный интеграл расходится.
Примечание: с пределом выражения 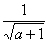
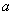
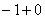
Пример 8: Решение: 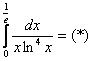
Подынтегральная функция терпит бесконечный разрыв в точке 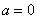
Примечание: Разбираемся в пределе выражения 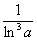
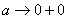
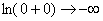
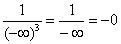
Пример 10: Решение: 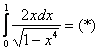
Подынтегральная функция терпит бесконечный разрыв в точке 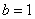
Пример 11: Решение: 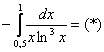
Подынтегральная функция терпит бесконечный разрыв в точке 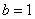
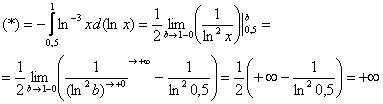
Несобственный интеграл расходится
Примечание: Разбираемся в пределе выражения 
Автор: Емелин Александр
(Переход на главную страницу)