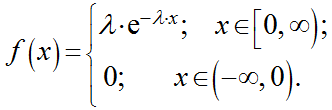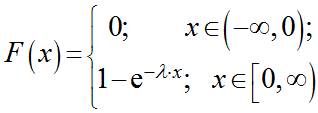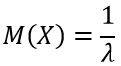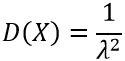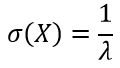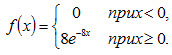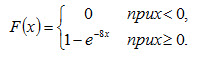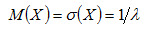случайная величина х распределена показательно с параметром равным 1 тогда р х 0 равна
Показательный (экспоненциальный) закон распределения
Непрерывная случайная величина X имеет показательный (экспоненциальный) закон распределения, если её плотность вероятности имеет вид:
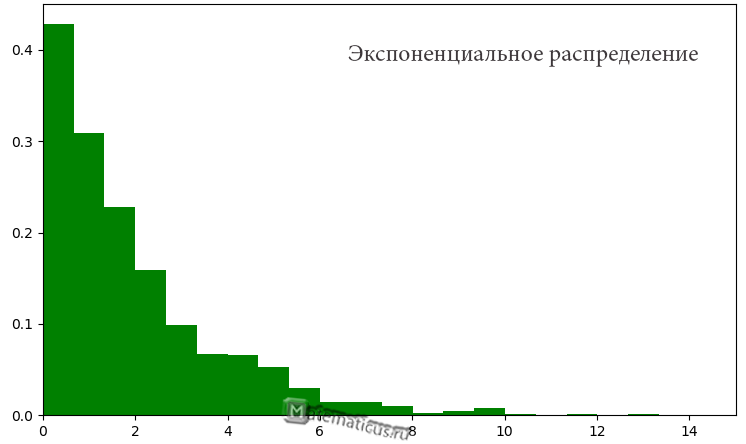
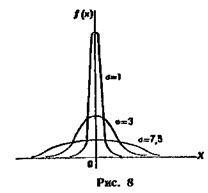
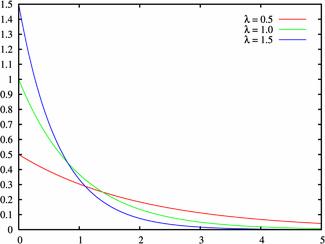
График плотности распределения случайной величины по показательному (экспоненциальному) закону
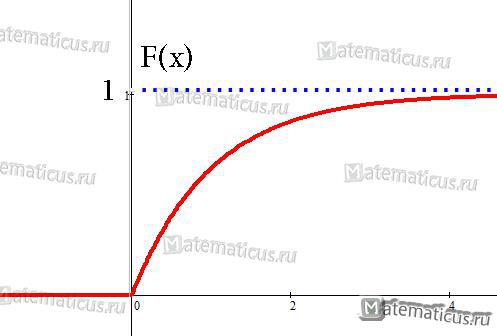
Функция распределения F(X) случайной величины X, распределенной по показательному закону, выражается формулой:
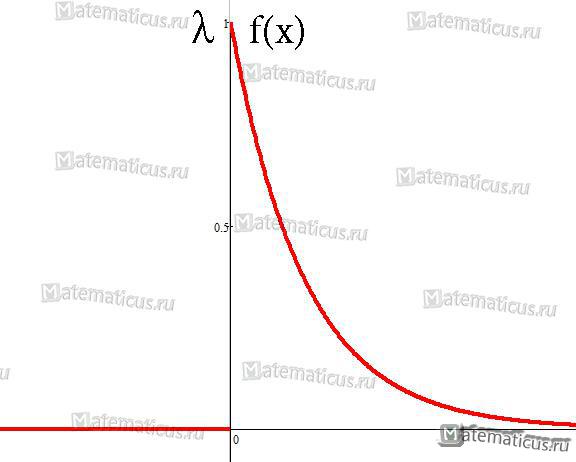
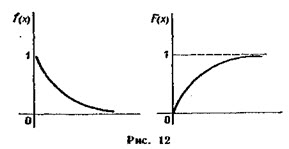
График функции распределения случайной величины по показательному (экспоненциальному) закону
λ — параметр распределения.
Математическое ожидание равно:
Дисперсия равна:
Среднеквадратическое отклонение (СКО) равно:
Вероятность того, что случайная величина X примет значение, принадлежащее интервалу (a, b), находится по формуле:
P(a −λa −e −λb
Показательное распределение применяют в теории массового обслуживания и надёжности, для моделирования времени безотказной работы, длительности безаварийной работы приборов и машин, демографии и т. д. Пример, устройство после включения ломается через короткий промежуток времени.
Случайная величина X – время работы лампы накаливания. Случайная величина подчинена показательному распределению. Определить вероятность того, что время работы лампы накаливания будет не меньше 800 часов, если среднее время работы лампы накаливания 400 часов.
В соответствии с условием задачи, математическое ожидание M(x) случайной величины X равно 400 часам, отсюда следует, что
Подставляя в формулу выше, получаем вероятность
Равномерный и показательный законы распределения непрерывной случайной величины
Как было сказано ранее, примерами распределений вероятностей непрерывной случайной величины Х являются:
Дадим понятие равномерного и показательного законов распределения, формулы вероятности и числовые характеристики рассматриваемых функций.
| Показатель | Раномерный закон распределения | Показательный закон распределения |
|---|---|---|
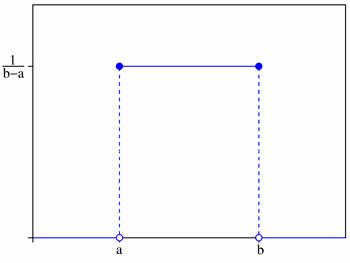
| Определение | Равномерным называется распределение вероятностей непрерывной случайной величины X, плотность которого сохраняет постоянное значение на отрезке [a;b] и имеет вид | Показательным (экспоненциальным) называется распределение вероятностей непрерывной случайной величины X, которое описывается плотностью, имеющей вид |
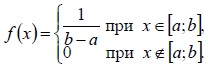 | 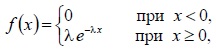 где λ – постоянная положительная величина | |
| Функция распределения | 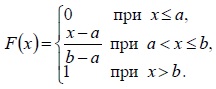 | 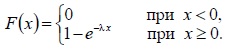 |
| Вероятность попадания в интервал | 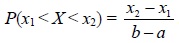 | 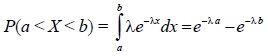 |
| Математическое ожидание | 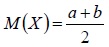 | 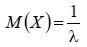 |
| Дисперсия | 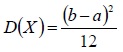 | 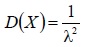 |
| Среднее квадратическое отклонение | 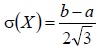 | 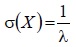 |
Примеры решения задач по теме «Равномерный и показательный законы распределения»
Задача 1.
Автобусы идут строго по расписанию. Интервал движения 7 мин. Найти: а) вероятность того, что пассажир, подошедший к остановке, будет ожидать очередной автобус менее двух минут; б) вероятность того, что пассажир, подошедший к остановке, будет ожидать очередной автобус не менее трех минут; в) математическое ожидание и среднее квадратическое отклонение случайной величины X – времени ожидания пассажира.
Решение. 1. По условию задачи непрерывная случайная величина X= <время ожидания пассажира>равномерно распределена между приходами двух автобусов. Длина интервала распределения случайной величины Х равна b-a=7, где a=0, b=7.
4. Находим для показательного распределения:
Другие статьи по данной теме:
Список использованных источников
2012 © Лана Забродская. При копировании материалов сайта ссылка на источник обязательна
Случайная величина х распределена показательно с параметром равным 1 тогда р х 0 равна
Нормальным называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью
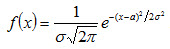
Замечание 1. Общим называют нормальное распределение с произвольными параметрами а и σ (σ >0).
Нормированным называют нормальное распределение с параметрами а=0 и σ =1.
Плотность нормированного распределения
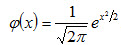
Эта функция табулирована (см. приложение 1).
Замечание 2. Функция F(x) общего нормального распределения
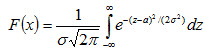
а функция нормированного распределения
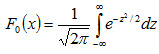
Функция F0(x) табулирована. Легко проверить, что
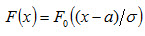
Замечание 3. Вероятность попадания нормированной нормальной величины Х в интервал (0, x) можно найти, пользуясь функцией Лапласа 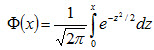
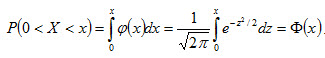
Замечание 4. Учитывая, что 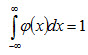
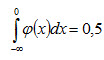
Следовательно, при х = а функция имеет максимум равный 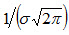
5. Разность х-а содержится в аналитическом выражении функции в квадрате, т. е. график функции симметричен относительно прямой х = а.
6. Исследуем функцию на точки перегиба. Найдем вторую производную:
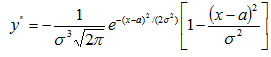
Легко видеть, что при х=а+σ и х=а— σ вторая производная равна нулю, а при переходе через эти точки она меняет знак (в обеих этих точках значение функции равно 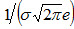
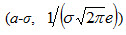
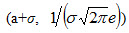
Как влияют на форму и расположение нормальной кривой значения параметров а и σ?
При а = 0 и σ = 1 нормальную кривую 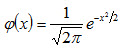
Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины X, которое описывается плотностью
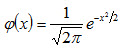
Примером непрерывной случайной величины, распределенной по показательному закону, может служить время между появлениями двух последовательных событий простейшего потока (показательный закон надежности).
Функция распределения показательного закона:
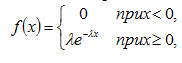
Графики плотности и функции распределения показательного закона:
Пример 1. Написать плотность и функцию распределения показательного закона, если параметр λ = 8.
Очевидно, искомая плотность распределения
Искомая функция распределения
Вероятность попадания в интервал (а, b) непрерывной случайной величины X, распределенной по показательному закону,
Пример 2. Непрерывная случайная величина X распределена по показательному закону
Числовые характеристики показательного распределения
Математическое ожидание показательного распределения равно обратной величине параметра λ:
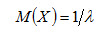
Дисперсия показательного распределения равна
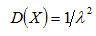
Среднее квадратическое отклонение показательного распределения равно
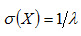
Математическое ожидание и среднее квадратическое отклонение показательного распределения равны между собой.
Пример 3. Непрерывная случайная величина X распределена по показательному закону
Распределение Пуассона и формула Пуассона
Краткая теория
Для пуассоновской случайной величины математическое ожидание и дисперсия совпадают с интенсивностью потока событий:
$$M(X)=lambda, quad D(X)=lambda.$$
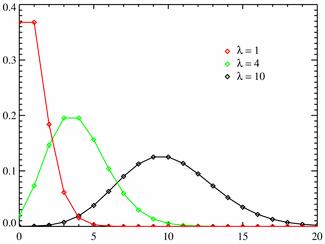
Распределение Пуассона – определение
Распределение Пуассона — вероятностное распределение дискретного типа, моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга. Другими словами, если событие происходит с некоторой периодичностью, то мы можем определить вероятность, что такое событие произойдёт n раз за интересующий нас период.
Параметр лямбда – λ
Распределение Пуассона зависит только от одного параметра – λ, данный параметр зависит от вероятности успешного события и общего количества событий.
Успешное событие: распределение Пуассона применяется только тогда, когда есть разделение на результат “да” и “нет”, например, лампочка перегорела: да – успешное событие; шина прокололась: да – успешное событие и так далее.
λ = n*p, где p – вероятность успешного события, а n – общее количество событий, для которых ведётся расчёт.
Например, если гроза проходит раз в месяц и мы хотим посчитать вероятность грозы за 24 месяца, то вероятность равна единице, а количество событий равно 24, откуда лямбда равна 24.
Можно считать по-другому, вероятность грозы в конкретный день – 1/30, количество событий – 730 дней, лямбда равна 24.3.
Пример
В тысяче ящиков с антоновками в одном попадается голден, какова вероятность, что в 5000 ящиках будет меньше 4 ящиков с яблоком голден?
Вероятность ящика с яблоком голден – 0.1% (1 ящик на 1000 = 1/1000, если в процентах – 1/1000 * 100 = 0.1%)
Общее количество событий – 5000 ящиков
Из вышесказанного следует:
λ = 5000 * 0.001 = 5
Функция вероятности (формула Пуассона)
Вероятность, что успешное событие произойдёт k раз:
Пример
В тысяче ящиков с антоновками в одном попадается голден, какова вероятность, что в 5000 ящиках будет 2 ящика с яблоком голден?
Из предыдущего примера мы знаем, что λ=5, теперь мы ищем вероятность, что k будет равно 2, для этого используем формулу функции вероятности:
Условия возникновения распределения Пуассона
Рассмотрим условия, при которых возникает распределение Пуассона.
Во-первых, распределение Пуассона является предельным для биномиального распределения, когда число опытов n неограниченно увеличивается (стремится к бесконечности) и одновременно вероятность p успеха в одном опыте неограниченно уменьшается (стремится к нулю), но так, что их произведение np сохраняется в пределе постоянным и равным λ (лямбде):

В математическом анализе доказано, что распределение Пуассона с параметром λ = np можно приближенно применять вместо биномиального, когда число опытов n очень велико, а вероятность p очень мала, то есть в каждом отдельном опыте событие A появляется крайне редко.
Во-вторых, распределение Пуассона имеет место, когда есть поток событий, называемым простейшим (или стационарным пуассоновским потоком). Потоком событий называют последовательность таких моментов, как поступление вызовов на коммуникационный узел, приходы посетителей в магазин, прибытие составов на сортировочную горку и тому подобных. Пуассоновский поток обладает следующими свойствами:
Характеристики случайной величины, распределённой по закону Пуассона
Характеристики случайной величины, распределённой по закону Пуассона:
математическое ожидание 
стандартное отклонение 
дисперсия 
Распределение Пуассона и расчёты в MS Excel
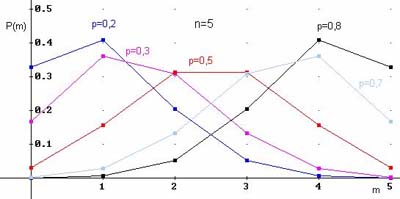
Вероятность распределения Пуассона P(m) и значения интегральной функции F(m) можно вычислить при помощи функции MS Excel ПУАССОН.РАСП. Окно для соответствующего расчёта показано ниже (для увеличения нажать левой кнопкой мыши).
MS Excel требует ввести следующие данные:
Почему Пуассон изобрел свое распределение?
Чтобы предсказывать количествобудущихсобытий!
Или более формально: чтобы предсказывать вероятность данного числа событий, происходящих в определенный интервал времени.
В продажах, например, “событие” это покупка (сам момент покупки, не просто выбор). Событием может быть количество посетителей в день на веб-сайте, кликов на рекламном объявлении в следующем месяце, число звонков в рабочее время или число людей, которые умрут от смертельных заболеваний в следующем году, и так далее.
Недостатки биномиального распределения
a) Биномиальная случайная величина бинарна — 0 или 1.
В примере выше у нас было 17 лайков в неделю. Это 17/7 = 2.4 человека в день и 17/(7*24) = 0.1 в час.
Если моделировать вероятность успеха в часах (0.1 человек в час), используя биномиальную случайную величину, получим, что в большем количестве часов лайков будет 0, а в некоторые часы ровно 1 лайк. Также возможно, что в час будет больше 1 лайка (2, 3, 5 и т.д.).
Проблема с биномиальным распределением в том, что оно не может содержать более одного события в единицу времени (1 час в примере).
Так может разделить 1 час на 60 минут и принять за единицу времени минуту? Тогда в 1 час поместится несколько событий. (Помним, что 1 минута содержит только ноль или одно событие).
Теперь проблема решена?
Вроде бы. Но что если в течение одной минуты мы получим несколько лайков? (например, кто-то поделился постом в Твиттере, и трафик вырос в эту минуту). Что тогда? Можно разделить минуту на секунды. Тогда единицей времени становится секунда, и в минуту помещается несколько событий. Но проблема бинарного контейнера будет существовать для все меньших единиц времени.
Дело в том, что биномиальная случайная величина может содержать несколько событий, если делить единицу времени на все меньшие единицы. В результате изначальная единица времени будет содержать более одного события.
Математически это означает n → ∞. Если предположим, что среднее значение фиксировано, тогда p → 0. В противном случае n*p — количество событий — чрезмерно возрастет.
Единица времени с использованием этого лимита может быть бесконечно мала. Больше не нужно беспокоиться о более чем одном событии в единицу времени. Так получается распределение Пуассона.
b) В биномиальном распределении количество попыток (n) должно быть известно заранее.
Нельзя посчитать вероятность успеха при помощи биномиального распределения, зная только среднее значение (17 человек в неделю). Нужно больше информации (n и p), чтобы использовать формулу.
Распределение Пуассона же не обязывает вас знать ни n ни p. Предположим, что n бесконечно велико, а p бесконечно мала. Единственный параметр распределения — значение λ (ожидаемое значение x). В реальной жизни чаще известно только значение (например, с 2 до 4 часов дня я принял 3 телефонных звонка), а не значения n и p.
Решение задачи на распределение Пуассона в Excel
Пример 1. Отдел технического контроля определил, что среднее число не соблюденных допусков в размерах производимых деталей составляет 6. Определить вероятности следующих событий обеими рассматриваемыми функциями (для сравнения результатов вычислений):
Вид таблицы данных:
Рассчитаем вероятность наличия трех и менее дефектов с помощью функций:
Для нахождения вероятности выбора детали с наличием ровно трех дефектов используем функции:
Для расчета вероятности точного совпадения третий аргумент задан в качестве логического ЛОЖЬ.
Как видно, результаты вычислений обеих функций идентичны.
Числовые характеристики случайной величины Х
Математическое ожидание распределения Пуассона
M[X] = λ
Дисперсия распределения Пуассона
D[X] = λ
Вероятность появления k событий за время длительностью t можно также найти по формуле Пуассона:
где λ — интенсивность потока событий, то есть среднее число событий, которые появляются в единицу времени.
а) оба элемента будут работать безотказно;
P(2) = P1(0)*P2(0) = 0,8187*0,6065 = 0,4966
б) только один элемент выйдет из строя.
P(1) = P1(0)*(1-P2(0)) + (1-P1(0))*P2(0) = 0.8187*(1-0.6065) + (1-0.8187)*0.6065 = 0.4321
Формула Пуассона
Давайте получим формулу Пуассона математически из формулы функции биномиального распределения.
Формулы: законы распределения случайных величин
В данном разделе вы найдете формулы по теории вероятностей, описывающие законы распределения дискретных и непрерывных случайных величин: биномиальный, Пуассона, экспоненциальный, равномерный, нормальный.
Каталог формул по теории вероятности онлайн
Законы распределения на этой странице
Дискретные случайные величины
Биномиальное распределение ДСВ
| $x_k$ | 0 | 1 | . | k | . | n |
| $p_k$ | $q^n$ | $n\cdot p \cdot q^ | $C_n^k \cdot p^k \cdot q^ | $p^n$ |
Здесь вероятности находятся по формуле Бернулли:
Числовые характеристики биномиального распределения:
Пуассоновское распределение ДСВ
Распределение Пуассона моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга.
Ряд распределения по закону Пуассона имеет вид:
| $x_k$ | 0 | 1 | . | k | . |
| $p_k$ | $e^<-\lambda>$ | $\lambda e^<-\lambda>$ | . | $\frac<\lambda^k> | . |
Вероятности вычисляются по формуле Пуассона:
Числовые характеристики для распределения Пуассона:
Геометрическое распределение ДСВ
Формула для вероятностей:
Ряд распределения геометрического закона:
| $x_k$ | 0 | 1 | 2 | . | k | . |
| $p_k$ | $p$ | $q\cdot p$ | $q^2 \cdot p$ | . | $q^k \cdot p$ | . |
Гипергеометрическое распределение ДСВ
$$M(X)=\frac
Непрерывные случайные величины
Показательное распределение НСВ
Экспоненциальное или показательное распределение — абсолютно непрерывное распределение, моделирующее время между двумя последовательными свершениями одного и того же события.
Числовые характеристики можно найти по формулам:
Равномерное распределение НСВ
Равномерный закон распределения используется при анализе ошибок округления при проведении числовых расчётов (например, ошибка округления числа до целого распределена равномерно на отрезке), в ряде задач массового обслуживания, при статистическом моделировании наблюдений, подчинённых заданному распределению.
Числовые характеристики равномерно распределенной случайной величины:
График плотности вероятностей:
Нормальное распределение или распределение Гаусса НСВ
Нормальное распределение, также называемое распределением Гаусса, – распределение вероятностей, которое играет важнейшую роль во многих областях знаний, особенно в физике.
Физическая величина подчиняется нормальному распределению, когда она подвержена влиянию огромного числа случайных помех. Ясно, что такая ситуация крайне распространена, поэтому можно сказать, что из всех распределений в природе чаще всего встречается именно нормальное распределение — отсюда и произошло одно из его названий.
Числовые характеристики для нормального распределения:
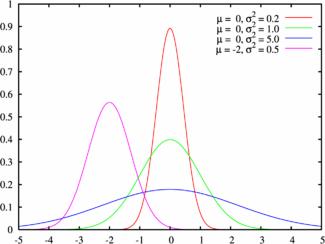
Пример графика плотности распределения для различных значений среднего и СКО:
Функция Лапласа определяется как:
Решенные задачи по теории вероятностей
Ищете готовые задачи по теории вероятностей? Посмотрите в решебнике: