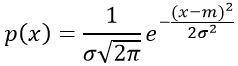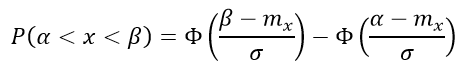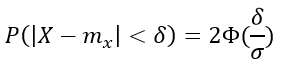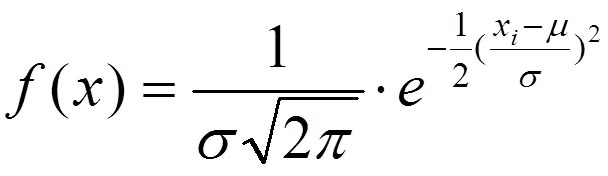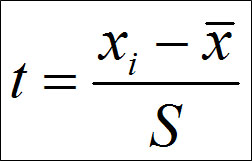случайная величина подчиняется нормальному закону распределения вероятностей с параметрами

Нормальный закон распределения

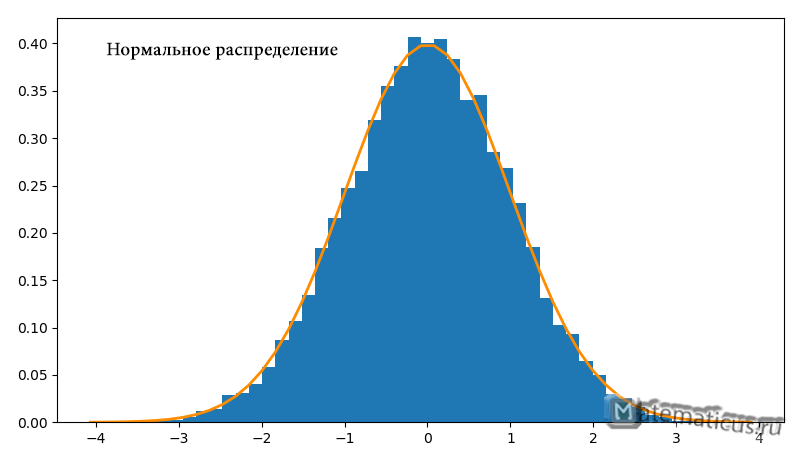
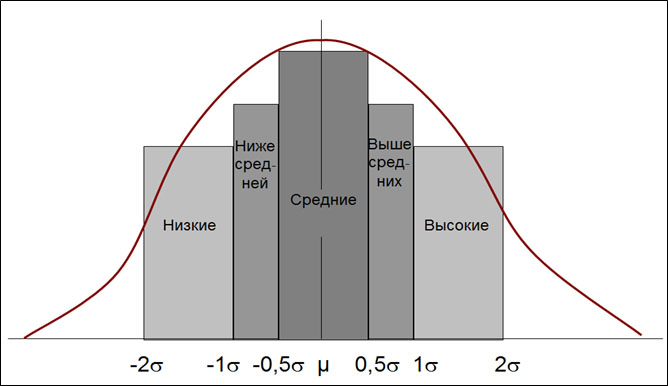
На рисунке ниже показан нормальный закон распределения случайной величины X в виде гистограммы.

Рисунок 1 — Пример нормального закона распределения

Случайная непрерывная величина X имеет нормальный закон распределения, если ее плотность распределения вероятности имеет выражение:

где m, σ — параметры распределения СВ;
m_xили m — математическое ожидание случайной величины,
— среднеквадратичное отклонение от величины a;
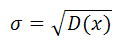
σ 2 — дисперсия.
Формула функции распределения СВ нормального закона определяется по формуле:

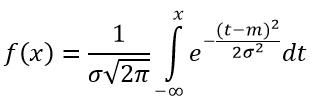
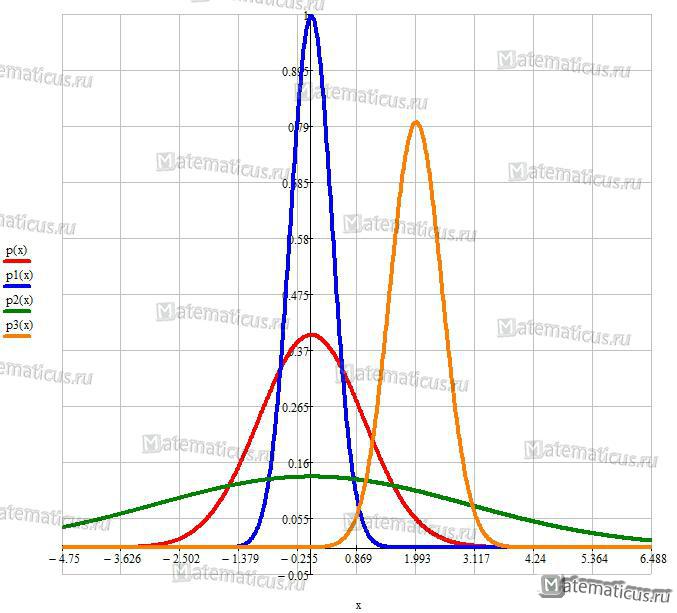
На рисунке 2 показана функция плотности нормального закона распределения при m=0 и σ=1;

При m=0 и σ=1 на рисунке 2 нормальное распределение СВ называется стандартным нормальным распределением СВ (таблица плотности вероятности нормальной случайной величины), плотность которого равна

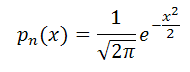
а функция распределения или функция Лапласа (таблица функции Лапласа)

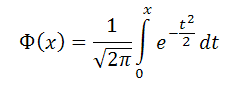
Вероятность попадания в заданный интервал (α; β) распределенной случайной величины по нормальному закону с параметрами a, σ вычисляется по формуле:

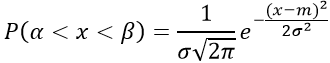
с использованием интеграла вероятности

Из этих соотношений легко получить вероятность отклонения распределения случайной величины X от своего математического ожидания m:

,где δ — величина отклонения.

Полагая в этой формуле δ=3σ, получаем

Замечание
Нормальный закон распределения СВ является основным (базовым), часто встречается на практике и его также называют законом Гаусса.

Используется для построения доверительных интервалов, применяется для моделирования разброса при стрельбе, измерения ошибок и т.д.

При n→∞ биномиальное распределение быстро начинает приближаться к нормальному закону распределения СВ.

Пример 1

Математическое ожидание и среднее квадратичес­кое отклонение нормально распределенной случайной величины X соответственно равны 20 и 5. Найти вероятность того, что в результате испытания X примет значение, заключенное в интервале (15, 25).
Решение

Так как функция Ф(х) нечётна:

По таблице функции Лапласа находим значение Ф(1) =0,3413

По таблице функции Лапласа находим значение Ф(1.41) =0,3413

Пример 3

На станке изготавливается некоторая деталь. Ее длина представляет собой случайную величину, распределенную по нормальному закону, и имеет среднее значение 20 см и среднее квадратическое отклонение равную 0,2 см. Найти вероятность того, что длина детали будет заключена между 19,7 см и 20.3 см

Решение

По таблице функции Лапласа находим значение Ф(1) =0,3413

Пример 4
Производится измерение диаметра вала без систематических (одного знака) ошибок. Случайные ошибки измерения X подчинены нормальному закону со средним квадратическим отклонением σ=10 мм. Найти вероятность того, что измерение будет произведено с ошибкой, не превосходящей по абсолютной величине 15 мм.

Решение

Математическое ожидание равно нулю, δ=15, σ=10, тогда

По таблице функции Лапласа находим значение Ф(1.5) =0,43319

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 4.5 / 5. Количество оценок: 4

Источник

Нормальный закон распределения

Нормальный закон распределения случайной величины

Значение для исследований в области физической культуры и спорта (ФКиС)

Нормальное распределение случайной величины (гауссово распределение, распределение Гаусса, распределение Гаусса-Лапласа) – одно из непрерывных распределений, имеющее основополагающую роль в математической статистике. Причинами это являются:

Однако в природе и в области ФКиС встречаются экспериментальные распределения, для описания которых модель нормального распределения малопригодна.

История изучения нормального распределения

Первые исследования по теории вероятностей проводили математик, механик, физик Блез Паскаль и математик Пьер Ферма в середине XVII века. Эти исследования выполнялись по просьбе Шевалье де Мере, азартного игрока в кости, который пытался понять природу выигрыша. В дальнейшем эти исследования заложили основы теории вероятностей (Дж. Гласс, Дж. Стэнли, 1976).

Дальнейшее развитие теория вероятностей получила в XVIII веке. В 1713 году была опубликована книга швейцарского математика Якоба Бернулли «Искусство предположений». В этой книге был рассмотрен ряд вопросов теории вероятностей. Якоб Бернулли ввёл значительную часть современных понятий теории вероятностей, а также изложил правила подсчёта вероятности для сложных событий и дал первый вариант «закона больших чисел», разъясняющего, почему частота события в серии испытаний не меняется хаотично, а в некотором смысле стремится к своему предельному теоретическому значению (то есть вероятности).

В последствии (в 1730 г.) шотландский математик Джеймс Стирлинг опубликовал формулу, аппроксимирующую произведение первых n чисел. Это позволило упростить решение ряда задач, которые встречаются в теории вероятностей. Однако все еще эти задачи оставались трудно разрешимыми.

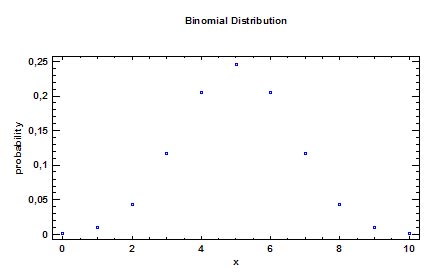
Эту задачу решил английский математик Абрахам де Муавр. В работе «Доктрина случайностей», которая была издана в 1738 году он привел формулу, аппроксимирующую биномиальное распределение события, вероятность которого была равна 0,5 (рис.1). То есть он нашел уравнение кривой, проходящей через точки графика, изображенного на рис. 1. Эта была формула, которую впоследствии стали называть формулой нормального распределения вероятностей. Появление формулы нормального распределения значительно упростило расчеты вероятностей событий.

В начале XIX века (в 1812 г.) французский математик, механик, физик и астроном Пьер-Симон де Лаплас обобщил результаты А. Муавра для произвольного биномиального распределения.

Рис.1. Биномиальное распределение

Одновременно с П. Лапласом в 1809 году немецкий математик, механик, физик и астроном Карл Фридрих Гаусс в сочинении «Теория движения небесных тел» использовал формулу нормального распределения для описания случайных ошибок, возникающих в результате многократных измерений движений небесных тел. К.Ф. Гаусс внес настолько большой вклад в разработку теории нормального распределения, что впоследствии это распределение стали назвать гауссово распределение или распределение Гаусса-Лапласса.

В начале ХХ века бельгийский математик, астроном и социолог Адольф Кетле одним из первых применил нормальный закон распределения случайной величины к анализу биологических и социальных процессов. Изучая распределение солдат американской армии по росту, Адольф Кетле обратил внимание, что распределение роста подчиняется нормальному закону. Он писал: «…Человеческий рост, изменяющийся, по-видимому, самым случайным образом, тем не менее подчиняется самым точным законам, и эта особенность свойственна не только росту, она проявляется также в весе, силе, быстроте передвижений человека, во всех его физических … и нравственных способностях. Этот великий принцип… разнообразящий проявление человеческих способностей…кажется нам одним из самых удивительных законов мира» (А.Кетле, 1911).

В настоящее время нормальное распределение широко используется в биологии, медицине, экономике и других областях науки.

Более подробно о методах статистической обработки данных рассказано в книгах:

Формула нормального распределения

Формула, описывающая нормальный закон распределения случайной величины, имеет следующий вид:

где: μ — генеральное среднее арифметическое; σ — генеральное стандартное отклонение, е — основание натуральных логарифмов, приблизительно равное 2,719, π — число, приблизительно равное 3,142; xi — конкретное значение признака.

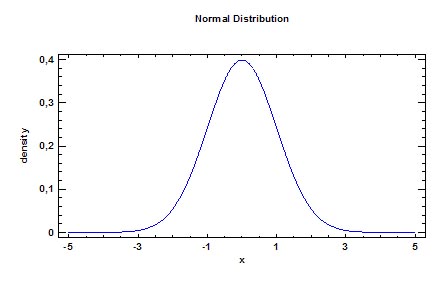
Пусть Вас не пугает эта формула. Сейчас мы с ней разберемся. Для начала давайте посмотрим, как выглядит график, построенный на основе этой формулы. Зададим значения μ=0 и σ=1. Хочу заметить, что μ и σ — это просто числа. Их еще называют параметрами распределения. Поэтому критерии, в формулу расчета которых входят параметры распределения называют параметрическими. Например, параметрическим критерием является t-критерий Стьюдента. В формулу расчета критерия Стьюдента входят параметры μ и σ. Кривая нормального распределения вероятностей имеет вид (рис.2).

Рис.2. График плотности вероятностей нормального распределения при μ=0 и σ=1.

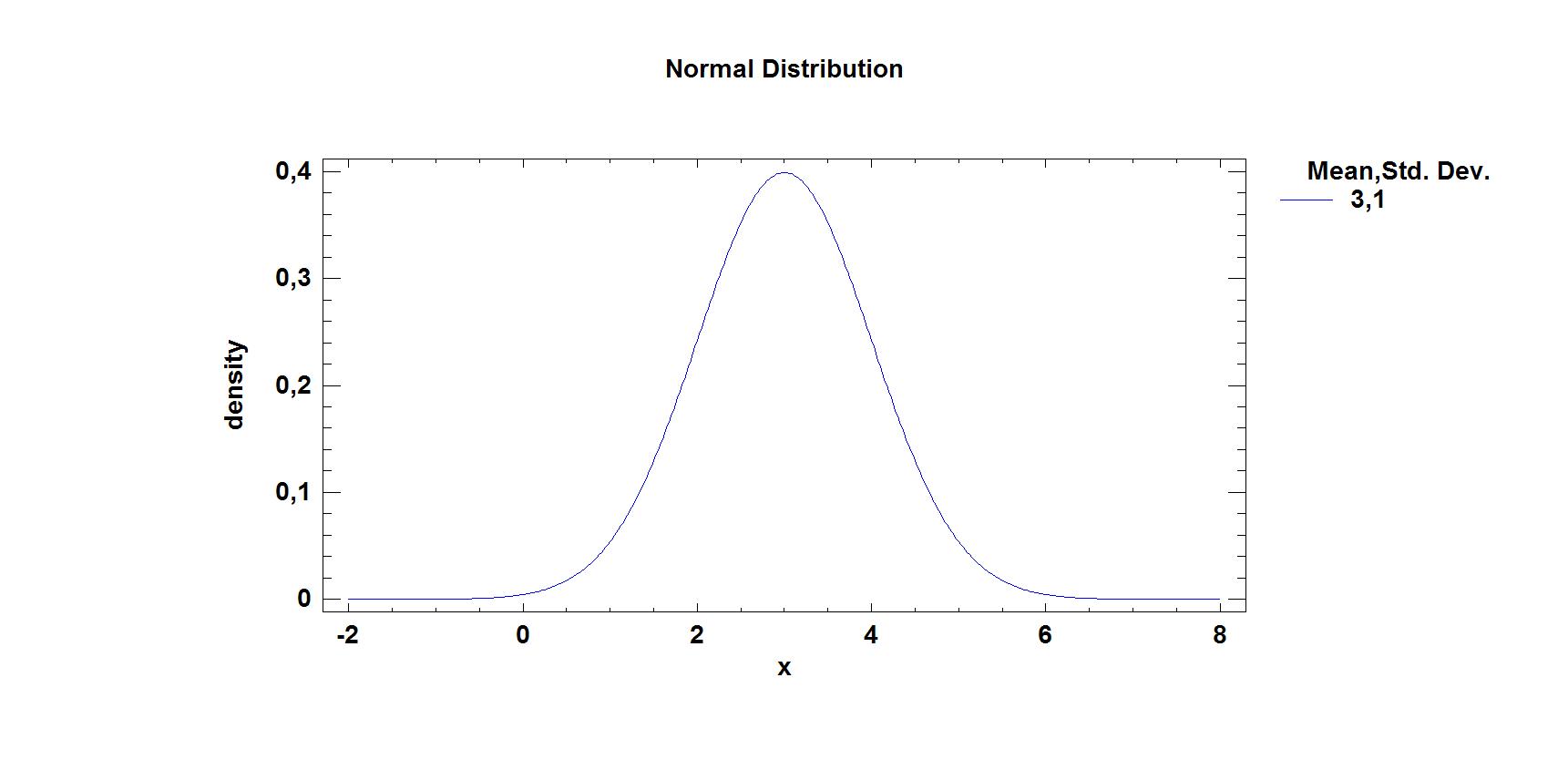
Если мы поменяем параметры, то получим следующее. Изменение параметра μ будет сдвигать график вдоль оси Х. Например при μ=3 график сместится вправо вдоль оси Х (рис.3).

Рис.3. График плотности вероятностей нормального распределения при μ=3 и σ=1.

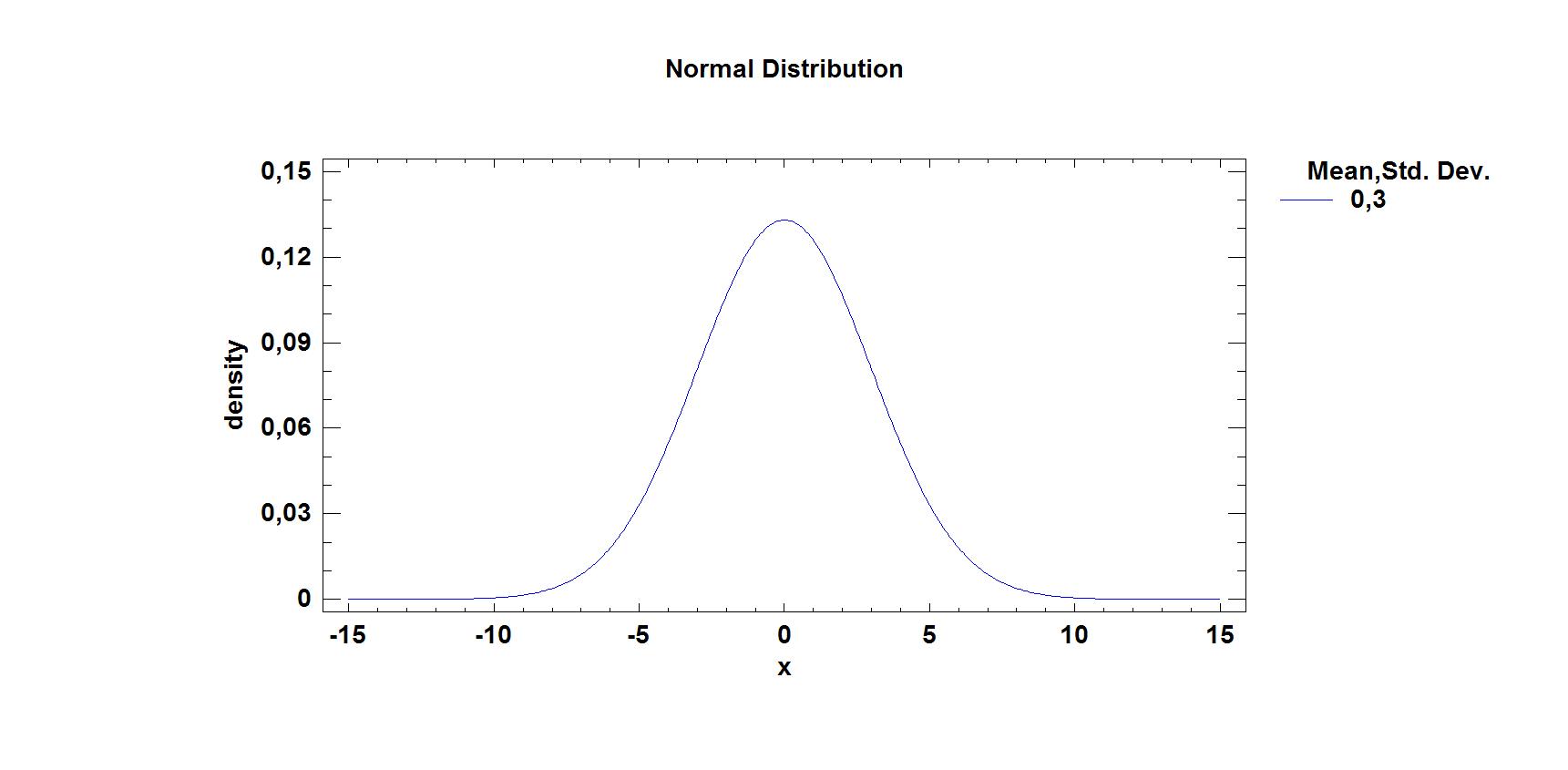
Рис.4. График плотности вероятностей нормального распределения при μ=0 и σ=3.

Свойства нормального распределения

Нормированное отклонение

В области математической статистики важное место занимает нормированное отклонение (t) – показатель, представляющий отклонение той или иной варианты от средней величины, отнесенное к значению стандартного отклонения. Нормированное отклонение рассчитывает по формуле:

Нормированное отклонение позволяет установить, на сколько «сигм» отклоняются варианты от среднего значения. Например, необходимо определить насколько «сигм» отклоняется значение роста человека, равное 180 см от среднего, если среднее арифметическое равно 170 см, а «сигма», то есть стандартное отклонение равно 10 см. Подставив эти значения в формулу, получим: t= (180-170)/10 = 1.

Ответ: значение роста человека, равное 180 см отклоняется от среднего на одну «сигму».

Нормированное нормальное распределение

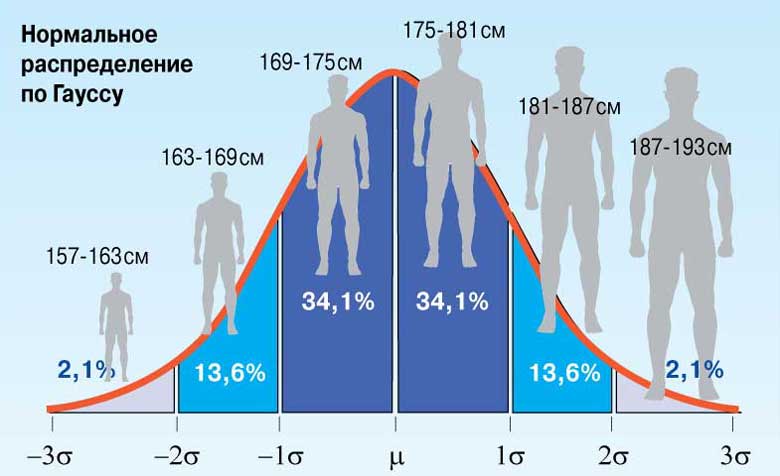
Рис.5. Нормированное нормальное распределение роста мужчин с параметрами: µ=0; σ = 1.

Формула нормального распределения описывает целое семейство кривых, зависящих от двух параметров μ и σ, которые могут принимать любые значения. Поэтому возможно бесконечно много нормально распределенных совокупностей.

Чтобы избежать неудобств, связанных с расчетами для каждого конкретного случая в до компьютерную эпоху было предложено использовать нормированное (стандартное) нормальное распределение, для которого были составлены подробные таблицы. Нормированное нормальное распределение имеет параметры: µ=0; σ = 1 (рис.1, 5). Это распределение получается, если пронормировать нормально распределенную величину Х по формуле:

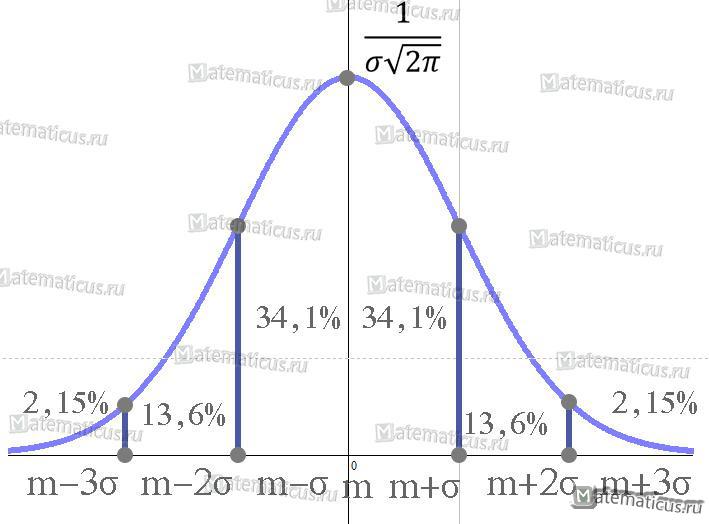
Для нормированного нормального распределения характерно, что в интервал µ± σ попадают 68 % всех результатов, в интервал µ± 2σ попадают 95% всех результатов, в интервал µ± 3σ попадают 99 % всех результатов.

Критерии согласия

Чтобы проверить, соответствует ли распределение нормальному закону, существует много методов.

Можно использовать свойства нормального распределения (равенство среднего, моды и медианы).

Однако более точные результаты дают критерии согласия. В зависимости от объема выборки (n) следует использовать различные критерии:

Источник

Нормальное распределение непрерывной случайной величины

Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.

Нормальное распределение: теория и практика

Вероятность встретить в выборке те или иные значение равна площади фигуры под кривой и в случае нормального распределения мы видим, что под верхом «колокола», которому соответствуют значения, стремящиеся к среднему, площадь, а значит, вероятность, больше, чем под краями. Таким образом, получаем то же, что уже сказано: вероятность встретить человека «нормального» роста, поймать рыбу «нормальной» массы выше, чем для значений, отличающихся в бОльшую или меньшую сторону. В очень многих случаях практики ошибки измерения распределяются по закону, близкому к нормальному.

Если копнуть глубже, то нормальное распределение можно найти в распределении многих показателях в системах связи (сигналы, шумы, помехи и другие), под нормальное распределение подгоняют многие финансовые показатели. Хотя следует подчеркнуть, что именно подгоняют, поскольку признаки нормальности в этих случаях часто бывают смещены.

Остановимся ещё раз на рисунке в начале урока, на котором представлена функция плотности нормального распределения. График этой функции получен при рассчёте некоторой выборки данных в пакете программных средств STATISTICA. На ней столбцы гистограммы представляют собой интервалы значений выборки, распределение которых близко (или, как принято говорить в статистике, незначимо отличаются от) к собственно графику функции плотности нормального распределения, который представляет собой кривую красного цвета. На графике видно, что эта кривая действительно колоколообразная.

Нормальное распределение во многом ценно благодаря тому, что зная только математическое ожидание непрерывной случайной величины и стандартное отклонение, можно вычислить любую вероятность, связанную с этой величиной.

Что влияет на график плотности нормального распределения

Чуть далее мы разберем довольно ужасную на первый взгляд формулу функции плотности нормального распределения. А пока остановимся на важнейших параметрах, связанных с этой формулой, которые влияют на вид графика плотности нормального распределения.

Коэффициент асимметрии (β 1 ). Если он равен нулю, то график плотности нормального распределения симметричен относительно среднего. Если он отличен от нуля, то распределение случайной величины несимметрично, причем, если коэффициент положителен, то правый хвост длиннее, а если отрицателен, то длиннее левый хвост. Это показано на графике снизу.

Коэффициент эксцесса (β 2 ). Характеризует остроту вершины графика плотности нормального распределения. Чем больше значение коэффициента, тем острее вершина. Это показано на графике снизу.

Подробнее о функции плотности нормального распределения

Функцию плотности нормального распределения непрерывной случайной величины можно найти по формуле:

,

Свойства функции плотности нормального распределения

Повторим знания о графиках функции плотности. Изменения среднего значения перемещают кривую функции плотности нормального распределения в направлении оси Ox. Если возрастает, кривая перемещается вправо, если уменьшается, то влево.

Вероятность попадания значения нормально распределённой случайной величины в заданный интервал

Интегральная функция нормального распределения:

.

Однако проблематично получить таблицы для каждой возможной комбинации среднего и стандартного отклонения. Поэтому одним из простых способов вычисления вероятности попадания нормально распределённой случайной величины в заданный интервал является использование таблиц вероятностей для стандартизированного нормального распределения.

Стандартизованным или нормированным называется нормальное распределение, среднее значение которого , а стандартное отклонение .

Функция плотности стандартизованного нормального распределения:

.

Интегральная функция стандартизованного нормального распределения:

.

На рисунке ниже представлена интегральная функция стандартизованного нормального распределения, график которой получен при рассчёте некоторой выборки данных в пакете программных средств STATISTICA. Собственно график представляет собой кривую красного цвета, а значения выборки приближаются к нему.

Для увеличения рисунка можно щёлкнуть по нему левой кнопкой мыши.

Стандартизация случайной величины означает переход от первоначальных единиц, используемых в задании, к стандартизованным единицам. Стандартизация выполняется по формуле

.

На практике все возможные значения случайной величины часто не известны, поэтому значения среднего и стандартного отклонения точно определить нельзя. Их заменяют средним арифметическим наблюдений и стандартным отклонением s. Величина z выражает отклонения значений случайной величины от среднего арифметического при измерении стандартных отклонений.

Открытый интервал

Таблица вероятностей для стандартизированного нормального распределения, которая есть практически в любой книге по статистике, содержит вероятности того, что имеющая стандартное нормальное распределение случайная величина Z примет значение меньше некоторого числа z. То есть попадёт в открытый интервал от минус бесконечности до z. Например, вероятность того, что величина Z меньше 1,5, равна 0,93319.

Пример 1. Предприятие производит детали, срок службы которых нормально распределён со средним значением 1000 и стандартным отклонением 200 часов.

Для случайно отобранной детали вычислить вероятность того, что её срок службы будет не менее 900 часов.

Решение. Введём первое обозначение:

— искомая вероятность.

Значения случайной величины находятся в открытом интервале. Но мы умеем вычислять вероятность того, что случайная величина примет значение, меньшее заданного, а по условию задачи требуется найти равное или большее заданного. Это другая часть пространства под кривой плотности нормального распределения (колокола). Поэтому, чтобы найти искомую вероятность, нужно из единицы вычесть упомянутую вероятность того, что случайная величина примет значение, меньше заданного 900:

Теперь случайную величину нужно стандартизировать.

Продолжаем вводить обозначения:

По этим данным условия задачи получаем:

.

По таблицам стандартизированной случайной величине (границе интервала) z = −0,5 соответствует вероятность 0,30854. Вычтем ее из единицы и получим то, что требуется в условии задачи:

.

Итак, вероятность того, что срок службы детали будет не менее 900 часов, составляет 69%.

Пример 2. В некотором городе среднегодовой доход семьи является нормально распределённой случайной величиной со средним значением 300000 и стандартным отклонением 50000. Известно, что доходы 40 % семей меньше величины A. Найти величину A.

Чтобы найти величину A, сначала составим интегральную функцию:

.

Поэтому составляем равенство

и находим его решение:

Ответ: доходы 40 % семей менее 287300.

Закрытый интервал

Подсказка: в этой задаче помимо нахождения вероятности попадания случайной величины в закрытый интервал (вероятность получения небракованной детали) требуется выполнить ещё одно действие.

Приближенный метод проверки нормальности распределения

Приближенный метод проверки нормальности распределения значений выборки основан на следующем свойстве нормального распределения: коэффициент асимметрии β 1 и коэффициент эксцесса β 2 равны нулю.

Коэффициент асимметрии β 1 численно характеризует симметрию эмпирического распределения относительно среднего. Если коэффициент асимметрии равен нулю, то среднее арифметрического значение, медиана и мода равны: и кривая плотности распределения симметрична относительно среднего. Если коэффициент асимметрии меньше нуля ( β 1 ), то среднее арифметическое меньше медианы, а медиана, в свою очередь, меньше моды () и кривая сдвинута вправо (по сравнению с нормальным распределением). Если коэффициент асимметрии больше нуля ( β 1 > 0 ), то среднее арифметическое больше медианы, а медиана, в свою очередь, больше моды () и кривая сдвинута влево (по сравнению с нормальным распределением).

Коэффициент эксцесса β 2 характеризует концентрацию эмпирического распределения вокруг арифметического среднего в направлении оси Oy и степень островершинности кривой плотности распределения. Если коэффициент эксцесса больше нуля, то кривая более вытянута (по сравнению с нормальным распределением) вдоль оси Oy (график более островершинный). Если коэффициент эксцесса меньше нуля, то кривая более сплющена (по сравнению с нормальным распределением) вдоль оси Oy (график более туповершинный).

Коэффициент асимметрии можно вычислить с помощью функции MS Excel СКОС. Если вы проверяете один массив данных, то требуется ввести диапазон данных в одно окошко «Число».

Коэффициент эксцесса можно вычислить с помощью функции MS Excel ЭКСЦЕСС. При проверке одного массива данных также достаточно ввести диапазон данных в одно окошко «Число».

Для коэффициента асимметрии β 1 :

,

— квантиль стандартного нормального распределения уровня ,

Для коэффициента эксцесса β 2 :

,

— квантиль стандартного нормального распределения уровня ,

Нормальное распределение и расчёты в MS Excel

Значения функции плотности f(x) и интегральной функции F(x) нормального распределения можно вычислить при помощи функции MS Excel НОРМ.РАСП. Окно для соответствующего расчёта показано ниже (для увеличения нажать левой кнопкой мыши).

MS Excel требует ввести следующие данные:

Решим ещё задачи на нормальное распределение

Решить задачу самостоятельно, а затем посмотреть решение

Решим ещё одну задачу вместе

Пример 6. О случайной величине X известно, что она нормально распределена, а вероятности того, что она составит 10 или меньше и больше 25, соответственно и . Найти среднее значение (математическое ожидание) случайной величины и её дисперсию.

Решение. Используем данные в условии задачи вероятности:

Пользуясь статистическими таблицами, находим:

Составляем систему из полученных равенств:

Решая систему, находим:

.

Источник