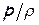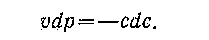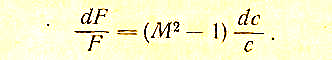статические параметры и параметры торможения

Параметры торможения

Газодинамические функции

Параметры состояния неподвижного газа, как известно, включают в себя давление p, температуру T и плотность r. Эти параметры называют истинными или термодинамическими. Иначе их называют статическими параметрами. Если газ движется, то перед неподвижно установленными приборами, напри­мер трубкой манометра или термометром он тормозится (рисунок 2.1). При торможении происходит сжатие газа, в результате чего местные значения па­раметров его состояния изменяются (увеличиваются) по сравнению с их зна­чениями в набегающем потоке. Такие параметры называют параметрами тор­можения или полными параметрами. Для того, чтобы отличить параметры тор­можения от статических при записи параметров они помечаются верхним индексом в идее звездочки «*». В то время как истинные параметры никаких дополнительных обозначений не имеют.

Рисунок 2.1 – Измерение давления и температуры

Объяснить повышение параметров достаточно легко. Дело в том, что при торможении потока вблизи чувствительного элемента измерительного прибора его кинетическая энергия стремиться к нулю и переходит во внутреннюю энергию и потенциальную энергию сил давления. Из-за этого давление и температура потока в месте торможения будут расти.

Соотношения для вычисления полных параметров могут быть получены из уравнения энергии с допущением о том, что процесс торможения энергоизолирован. Величина полной температуры связана со статической следующим выражением:

с – скорость потока, м/с;

Значение полного давления (если предположить, что r=const) находится по следующему соотношению:

где – статическое давление, Па;

С первого взгляда может показаться, что полные параметры представляют собой просто некачественные измерения параметров потока. Однако в реальности имеют большое практическое значение, поскольку характеризуют не только параметры состояния, но и энергетику потока.

А как же измерить истинные значения параметров потока? Для этого измерительные устройства следовало бы перемещать вдоль течения со скоростью газа так, чтобы относительно потока они оказались неподвижными. Однако понятно, что на практике такой подход неосуществим.

Практически для измерения давления в потоке применяют отверстие, просверленное строго перпендикулярно потоку в стенке канала вдоль которого течет газ. Поскольку статическое давление передается без изменений через пограничный слой, то через отверстие замеряется точно такое же термодинамическое давление, как и в набегающем потоке. Такой метод измерения применим только в том случае если по сечению трубы давление постоянно. Это наблюдается в прямолинейных трубах при движении потока без вращения, т.е линии тока прямые. Если же канал образует поворот или поток движется по винтовой линии, то давление в поперечном сечении распределено неодинаково и его нужно замерять в разных точках по сечению. Для этой цели применяют трубку статического давления, которую помещают в любое место потока. В этой трубке отверстие, через которое измеряется статическое давление, расположено строго перпендикулярно боковой поверхности трубки.

Рисунок 2.2 – Насадок для измерения статического давления

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Параметры торможения. Критическая скорость. Число Маха

Параметры торможения. Критическая скорость. Число Маха

Параметры торможения. Критическая скорость. Число Маха. Анализ и расчет гидродинамических и термодинамических свойств газового потока с использованием уравнения Бернулли значительно упрощается, если на линии потока имеется точка, в которой скорость газа становится равной нулю. Например, если газ вытекает из пласта (рис. 15.2), то скорость пласта достаточно велика, чтобы ее можно было считать равной нулю, поэтому на участке линии потока пласта считается, что скорость газа равна zero. In кроме того, уравнения Бернулли (15.30), (15.32) и (15.33) в этой строке представлены следующим образом: Где p0, p0, T0 и # 0-значения соответствующих величин в резервуаре.

В общем случае в действительном потоке не может быть такой точки, чтобы скорость газа была равна нулю. Людмила Фирмаль

Возмущение в нем не может распространяться вверх или вниз, и объекты, введенные в сверхзвуковой поток, могут воздействовать только на ту часть потока, которая расположена ниже по течению. (рис.15.4). Приведен пример использования термодинамической формы уравнения Бернулли. Полет самолета при низких температурах опасен из-за обледенения крыльев и fuselage. In в частности, обледенение стенок кабины командира усложняет управление самолетом (рис.15.5).

Частицы газа втекают в тело и не успевают подготовиться к обтеканию, только вблизи передней части тела изменяется его скорость, образуя ударный(компрессионный) слой. Людмила Фирмаль

Смотрите также:

Возможно эти страницы вам будут полезны:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник

Параметры торможения

В потоке жидкости могут существовать точки или области, скорость жидкости W в которых равна нулю. Это может быть критическая точка на поверхности обтекаемого тела, в которой по определению W=0. При истечении жидкости через отверстие или сопло из ёмкости большого объёма, жидкость внутри этой ёмкости практически везде, кроме области, непосредственно прилегающей к отверстию или соплу, можно считать неподвижной, принимая, что W=0.

или ,

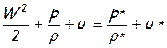
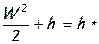
где удельная потенциальная энергия выражена через энтальпию жидкости .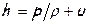

Поскольку в точке торможения кинетическая энергия жидкости полностью переходит в потенциальную (W®0), то в этой точке энтальпия h * определяет уже не только потенциальную энергию, но и весь запас энергии единицы массы жидкости, т.е. её полную удельную энергию. Поэтому энтальпию в точке торможения или «энтальпию торможения» называют ещё «полной энтальпией».

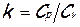
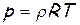
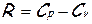
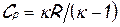
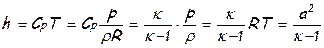
В случае течения совершенного газа, который имеет постоянные теплоёмкости C_p и C_v, показатель адиабаты (изоэнтропы) , удовлетворяет уравнению состояния (уравнению Менделеева-Клапейрона) , где 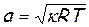удельная газовая постоянная , с учетом очевидного соотношения энтальпия может быть представлена следующим образом:

,

где — скорость звука.

Тогда уравнение энергии для элементарной струйки примет вид:

или ,

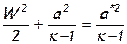
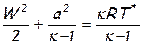
При изотермическомизоэнтропийном торможении, что, очевидно, может иметь место только в случае энергоизолированного течения идеальной несжимаемой жидкости, будет происходить изменение соотношения только внешних механических составляющих энергии жидкости, т.е. будет происходить лишь переход «кинетической энергии направленного движения» в «потенциальную энергию давления».

Полная температура определяется соотношением

,

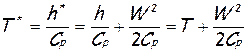
Используя уравнение изоэнтропы, выразим плотность жидкости r через давление в потоке p

;

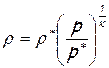
отношение давления к плотности

;

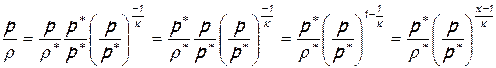
и из уравнения энергии для элементарной струйки «на участке торможения»:

,

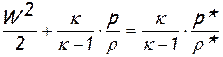
получим соотношение, однозначно связывающее основные газодинамические параметры движущейся жидкости – давление p и скорость W, с параметрами изоэнтропийного торможения:

.

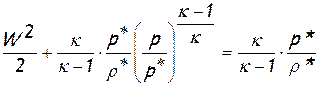
Последнее уравнение обычно называют интегральным уравнением Бернулли или «интегралом» Бернулли для сжимаемой жидкости, поскольку оно может быть получено в результате интегрирования вдоль элементарной струйки (линии тока) непосредственно дифференциального уравнения движения идеальной жидкости. В отличие от приведенного выше уравнения энергии, которое связывает три параметра (скорость, давление и плотность), интеграл Бернулли связывает два параметра (скорость и давление), но справедлив только для изоэнтропийного течения. Напомним, что уравнение энергии составлено для энергоизолированной элементарной струйки и справедливо также и для неизоэнтропийных течений.

В случае несжимаемой жидкости (r=const) интеграл Бернулли принимает особенно простой вид:

,

или ,

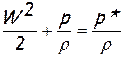
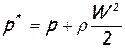
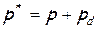
Любой реальный процесс торможения жидкости происходит с необратимыми потерями энергии, т.е. неизоэнтропийно (dS>0). Величина потерь в том или ином случае может быть ничтожно малой, но в любом реальном процессе эти потери есть.

В заключении следует особо подчеркнуть, что при определении параметров торможения не обязательно имеется в виду реальное торможение потока. Также не обязательно приписывать им смысл параметров жидкости в некоторой конкретной точке торможения, которой в общем случае в рассматриваемом потоке может и не быть.

Параметры торможения следует понимать как расчетные параметры, которые мы получили бы, если бы смогли полностью затормозить рассматриваемый поток жидкости без необратимыхпреобразований механической энергии.

Параметры торможения можно формально вычислить в любой точке потока по соответствующим формулам. Так, например, параметры изоэнтропийного торможения можно вычислить в данной точке потока, хотя само течение может и не быть изоэнтропийным. Вместе с тем важно отметить, что параметры изоэнтропийного торможения являются физическими понятиями, т.е. соответствующие параметры могут быть измерены, хотя, конечно, с определенной погрешностью, так как при измерении нельзя полностью исключить теплообмен. Измерение параметров изоэнтропийного торможения имеет большое значение при проведении газодинамических экспериментов.

& [1] с.16…19; 29…31. [2]найти самостоятельно не составит труда!

& [3]с.40…41. [4] с.53. [5]с.415…418. [6]с.133…135. [7] с.47…48. [8]с.188…200.

23. Пневмометрические приборы

Из всех измерений производимых в экспериментальной газовой динамике, измерения скоростей и давлений являются наиболее важными и наиболее широко применяемыми. Разработано множество различных методов определения скоростей и давлений, создано огромное количество конструкций приборов. Однако среди этого разнообразия наибольшее значение в экспериментальной практике имеет пневматический или пневмометрический способ или метод, основанный на измерении давления в определенных точках, на поверхности внесенных в поток измерительных приборов. Такие пневмометрические приборы называются насадками или зондами.

Основное требование к пневмометрическим приборам заключается в том, что бы величина изменения давления, вызванная внесением в поток прибора, была достаточно мала по сравнению с самим измеряемым давлением (разностью давлений). Поскольку для любого насадка или зонда размеры области и интенсивность возмущения находятся в прямой зависимости от размеров прибора, то указанное выше требование сводится, по сути, к требованию минимизации размеров прибора, а точнее – уменьшения отношения площадей поперечного сечения приёмной части прибора и поперечного сечения потока. В идеале это отношение должно быть исчезающе малым.

Насадки, служащие для измерения только полных давлений, называются трубками полного давления (ТПД) или трубками Пито. Последнее название закрепилось в зарубежной научно-технической литературе, а в отечественной трубками Пито обычно называют только насадки с характерной Г-образной формой. Поскольку полное давление (давление торможения) можно измерить отбором давления в критической точке помещенного в поток тела практически любой формы, то это привело к использованию в исследовательской практике большого многообразия форм и размеров ТПД. Кроме упомянутой Г-образной ТПД (с различной формой приемной части – цилиндрической, сферической, конической и пр.) широко используются цилиндрическая ТПД (приёмное отверстие расположено на боковой поверхности цилиндрической трубки) и так называемая ТПД с протоком, основным достоинством которой является нечувствительность к углам скоса потока (до ± 40 o … 50 o ) в широком диапазоне чисел Маха.

Подробную информацию о пневмометрических приборах, методах и технике газодинамического эксперимента можно найти в специальной литературе (см. [3, 11…14] из списка дополнительной литературы).

Источник

Полные параметры рабочего тела

При рассмотрении движущегося потока следует различать статические и полные параметры рабочей среды. Статическими называются параметры (давление, температура и другие) в потоке, движущемся с некоторой скоростью С. Чтобы точно измерить статические параметры, измерительные приборы должны перемещаться в потоке с одинаковой с ним скоростью,

Если поток затормозить каким-либо образом, чтобы скорость его стала равной нулю, то параметры в потоке изменяются, так как ее кинетическая энергия при торможении потока преобразуется в потенциальную.

Параметры потока, заторможенного в изоэнтропийном процессе до нулевой скорости, называются полными параметрами, или параметрами торможения. Полные параметры имеют в обозначении индекс-звездочку (*). При изоэнтропийном процессе торможения полная энергия рабочей среды остается постоянной, поэтому для любого сечения канала можно записать:

. (2.15)

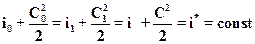
Учитывая, что i = C_pT, после деления каждого члена уравнения (2.15) на Ср получим зависимость между полной и статической температурами

. (2.16)

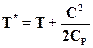
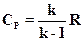
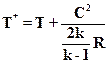
Для идеального газа , тогда .

Полное давление определяется из уравнения изоэнтропии :

. (2.17)

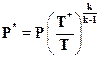
Уравнение (2.17) можно представить в виде:

,

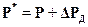
где 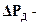разность между полным и статическим давленииями, определяемая с помощью трубок скоростного напора.

Для несжимаемой жидкости (или для сжимаемой среды при М

Дата добавления: 2015-07-18 ; просмотров: 2718 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Параметры торможения

Из уравнения энергии следует, что для энергоизолирован­ного течения газа (обмен механической работой и теплом. с внешней средой отсутствует) сумма энтальпии и кинети­ческой энергии для любого сечения потока постоянна, т, е,

Очевидно, что в сечении, где поток тормозится (с= 0), энтальпия будет наибольшей. Энтальпию, соответствующую заторможенному потоку, называют полной энтальпией, или энтальпией торможения и. обозначаютh*. Таким образом,

Получаемая при таком торможении температура газа назы­вается также полной температурой, или температурой тормо­жения и обозначается Т*

Газ в заторможенном состоянии характеризуется также давлением р*, называемым полным, или давлением торможе­ния, и плотностью ρ*. Полное давление газар* определяется из предположения, что торможение газа не только энергоизолированно, но и происходит без трения. Это позволяет исполь­зовать для установления связи между различными полными параметрами и действительными параметрами, иногда назы­ваемыми статическими, уравнение идеальной адиабаты:

В газовой динамике для характеристики свойств газовых потоков используется число Маха(М), равное отношению скорости потока в сечении к скорости звука в этом же сече­нии. Из курса физики известно, что скорость звука зависит от свойств газа и его температуры и подсчитывается по формуле:

Воспользовавшись этой формулой для скорости звука и известным из термодинамики соотношением

Отсюда видно, что отношение параметров торможения к статическим является функцией числа М.

Течение газон через сопла и диффузоры

Движение газа в каналах имеет большое практическое значение. Так, в случае, когда необходимо преобразовать по­тенциальную энергию потока и кинетическую, используются сопла. Преобразование кинетической энергии потока в потен­циальную осуществляется в диффузорах.

Соплами называются каналы, в которых происходит уве­личение скорости потока и уменьшение давления. Газ, проте­кая по соплу, расширяется.

Диффузорами называются каналы, в которых скорость. потока уменьшается, а давление растет. Газ в процессе тече­ния по диффузору сжимается.

Для того чтобы определить форму сопел и диффузоров, не­обходимо знать зависимость площади поперечного сечения. канала от параметров газового потока. Такую зависимость можно получить, используя уравнения неразрывности, движе­ния и процесса.

Последовательно логарифмируя и дифференцируя уравне­ние неразрывности

Процесс течения газа по каналу энергетически изолиро­ван и считается идеальным, т. е. происходящим без трения. Для такого течения в соответствии с уравнением Бернулли

Подставляя в это выражение dp из уравнения Бернулли, получим

Объединив это выражение с уравнением расхода, получим уравнение, связывающее изменение площади поперечного се­чения канала с изменением скорости:

Из этого уравнения видно, что дозвуковой поток (М 0) и разгоняться(dc>0) в сужающемся канале(dF а, М>\) будет тормозиться(dc 0) в расши­ряющемся канале(dF>0). Таким образом, форма диффузо­ра или сопла будет зависеть от числаМ потока на входе.

Рис. Форма диффузоров и сопел: а) дозвуковой диффузор; б) дозвуковое сопло; в)сверхзвуковое сопло.

В компрессорах и турбинах, как правило, поток газа на входе имеет входе в каналы имеет скорость, меньшую, чем скорость звука в этом сечении. Поэтому в качестве диффузора используется расширяющийся канал. Форма сопла зависит от того, до какой скорости раз­гоняется в нем поток. Если поток разгоняется до скоро сти, меньшей, чем скоростьз вука, или равной скоростивука, то сопло должно быть сужающимся. Увеличение скорости потока сверх скорости звука возможно, если сопло будет иметь сужающийся участок, на выходе из которого скорость потока будет равна скорости звука, и следующий за ним расширяющийся участок для увеличения скорости сверхзвукового потока (рис. ). Сопло такой фор­мы часто называют соплом Лаваля.

Изменение параметров газа при движении его вдоль соп­ла Лаваля может быть установлено с помощью уравнений энергии и процесса, Скорость газа в каком-либо сечении сопла определяется по уравнению энергии для мпгрплполироипппого потока

где h*— энтальпия торможения газа на входе в сопло;

Отношение температур может быть заменено с помощью уравнения процесса отношением давлений

При движении газа вдоль сопла скорость газа растет, а давление и температура уменьшаются (рис. ). В соответ­ствии с температурой уменьшается и скорость звука. В самом узком сечении, где скорость потока становится равной ско­рости звука, устанавливается критический режим течения. Все параметры в этом сечении называются критическими.

Температура в критическом сечении Т_кр определяется из условия, что в этом сечении

зависит лишь от рода газа (k, R) и температуры торможения на входе в сопло.

Давление, которое установится в критическом сечении,

Таким образом, отношение давления в критическом сече­нии к давлению торможения на входе в канал, обозначае­мое β_КР, зависит только от атомности газа:

Обычно, когда рассматривается истечение газа из сопла, задаются параметры газа на входе в сопло (р₁*, Т₁*) и давле­ние среды(р₂), в которую происходит истечение.

Сравнение располагаемой степени расширения газа (р₁*/р₂) с критической (1/ β_КР) позволяет установить, какой характер течения, будет на выходе из сопла и какую форму должно иметь сопло. Так, если

поток на выходе из сопла будет дозвуковой и сопло должно иметь форму сужающегося канала. При равенстве

сужающемся сопле будет достигнута звуковая скорость. Сверхзвуковая скорость может быть достигнута лишь в сопле Лаваля при условии, что

Секундный массовый расход газа через сопло может быть подсчитан по выходному сечению:

Для анализа влияния различных факторов удобно выра­зить массовый расход через параметры на входе в сопло и степень расширения газа в нем. Для этого воспользуемся уравнением адиабаты

полученным выше выражением для скорости с, и уравнением состояния

Если степень расширения р₁*/р₂ больше критической (1/Р_кр), то расход газа удобнее определять через критическое сечение, подставив в формулу дляG вместо отношенияp₂/ p₁* величину β_КР. Тогда после преобразований получим

Источник