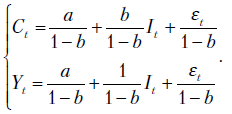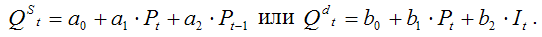структурный параметр называется сверхидентифицируемым если
Одновременные уравнения. Методы идентификации
7.3. Структурная и приведенная формы системы одновременных уравнений
В кейнсианской модели (7.1) переменная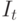 
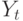
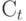
и переменные 
и 
существенно различаются. Первая переменная формируется под воздействием внешних факторов, большинство из которых относится к политической надстройке, создающей условия для роста инвестиций, и называется экзогенной переменной. Остальные переменные модели определяются из уравнений (7.1), т.е. внутри модели, и называются эндогенными переменными.
Если система уравнений помимо экзогенных и эндогенных переменных содержит еще и значения эндогенных переменных, полученные в предыдущие периоды времени, то такие значения называют лаговыми переменными, или предопределенными переменными. Тогда в приведенной форме системы следует выражать эндогенные переменные через экзогенные и лаговые переменные.
Модернизируем кейнсианскую модель, предполагая, что даже при сильных изменениях совокупного продукта обществу будет трудно сразу приспособиться к новому уровню потребления и большую роль при этом будет играть сложившийся в прошлые периоды стереотип потребления. То есть предположим, что функция потребления имеет вид
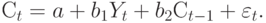 | (7.5) |
В рассматриваемый период времени 
уровень потребления в прошлый период времени считается известным, поэтому переменная 
является предопределенной. Приведенная форма модернизированной кейнсианской модели будет содержать в правой части переменные и .
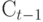
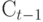
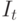
7.4. Косвенный и двухшаговый методы наименьших квадратов и проблема идентифицируемости
Метод, с помощью которого мы выше определили неизвестные структурные коэффициенты модели, называется косвенным методом наименьших квадратов. Суть его состоит в том, что сначала систему структурных уравнений преобразуют к приведенной форме. Затем коэффициенты приведенной формы рассчитывают по методу наименьших квадратов, и наконец, находят структурные коэффициенты из соотношений, связывающих приведенные и структурные коэффициенты уравнений.
Запишем приведенную систему уравнений (7.3) в несколько ином виде
Одновременные уравнения. Методы идентификации
7.3. Структурная и приведенная формы системы одновременных уравнений
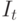
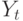
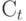
В кейнсианской модели (7.1) переменная и переменные и существенно различаются. Первая переменная формируется под воздействием внешних факторов, большинство из которых относится к политической надстройке, создающей условия для роста инвестиций, и называется экзогенной переменной. Остальные переменные модели определяются из уравнений (7.1), т.е. внутри модели, и называются эндогенными переменными.
Если система уравнений помимо экзогенных и эндогенных переменных содержит еще и значения эндогенных переменных, полученные в предыдущие периоды времени, то такие значения называют лаговыми переменными, или предопределенными переменными. Тогда в приведенной форме системы следует выражать эндогенные переменные через экзогенные и лаговые переменные.
Модернизируем кейнсианскую модель, предполагая, что даже при сильных изменениях совокупного продукта обществу будет трудно сразу приспособиться к новому уровню потребления и большую роль при этом будет играть сложившийся в прошлые периоды стереотип потребления. То есть предположим, что функция потребления имеет вид
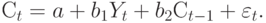| (7.5) |
В рассматриваемый период времени уровень потребления в прошлый период времени считается известным, поэтому переменная является предопределенной. Приведенная форма модернизированной кейнсианской модели будет содержать в правой части переменные и .
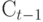
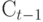
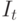
7.4. Косвенный и двухшаговый методы наименьших квадратов и проблема идентифицируемости
Метод, с помощью которого мы выше определили неизвестные структурные коэффициенты модели, называется косвенным методом наименьших квадратов. Суть его состоит в том, что сначала систему структурных уравнений преобразуют к приведенной форме. Затем коэффициенты приведенной формы рассчитывают по методу наименьших квадратов, и наконец, находят структурные коэффициенты из соотношений, связывающих приведенные и структурные коэффициенты уравнений.
Запишем приведенную систему уравнений (7.3) в несколько ином виде
Структурная и приведённая формы системы одновременных уравнений. Идентификация модели
Структурными уравнениями называются уравнения, из которых состоит исходная система одновременных уравнений. В данном случае система имеет структурную форму.
Структурная форма системы одновременных уравнений непосредственно характеризует реальный экономический процесс.
Структурными коэффициентами или параметрами называются коэффициенты уравнений структурной формы системы одновременных уравнений.
Структурные уравнения могут быть представлены либо поведенческими уравнениями, либо уравнениями-тождествами.
Поведенческие уравнения характеризуют все типы взаимодействия между эндогенными и экзогенными переменными в структурной форме системы одновременных уравнений.
В поведенческих уравнениях значения параметров являются неизвестными и подлежат оцениванию.
Примером поведенческого уравнения являются уравнение спроса или уравнение предложения в модели спроса-предложения:
Тождествами называют равенства, которые выполняются во всех случаях.
Отличительной чертой тождеств является то, что их вид и значения параметров известны, и они не содержат случайной компоненты.
Примером уравнения-тождества является тождество равновесия в модели спроса-предложения:
Для того чтобы определить неизвестные структурные коэффициенты системы одновременных уравнений необходимо перейти к приведённой форме системы.
Приведённой формой системы одновременных уравнений называется система независимых уравнений, в которой все эндогенные переменные выражены только через экзогенные или предопределённые переменные и случайные компоненты, например:
Приведёнными коэффициентами или параметрам называются коэффициенты приведённой формы системы одновременных уравнений.
Оценки неизвестных приведённых коэффициентов можно рассчитать с помощью классического метода наименьших квадратов, а уже на их основе определить оценки структурных коэффициентов.
При переходе от структурной формы системы одновременных уравнений к приведённой форме может возникнуть проблема идентификации модели.
Проблема идентификации состоит в возможности численной оценки неизвестных коэффициентов структурных уравнений по МНК-оценкам коэффициентов приведённых уравнений.
Исходная система одновременных уравнений называется идентифицированной, если все её уравнения точно идентифицированы.
Уравнение называется точно идентифицированным, если по оценкам коэффициентов приведённой формы системы одновременных уравнений можно однозначно найти оценки коэффициентов структурной формы системы одновременных уравнений.
Признаком идентифицированности системы одновременных уравнений является равенство между количеством уравнений, определяющих структурные коэффициенты, и количеством этих коэффициентов, т. е. квадратная форма структурной системы уравнений.
Исходная система одновременных уравнений называется сверхидентифицированной, если среди уравнений модели есть хотя бы одно сверхидентифицированное.
Уравнение называется сверхидентифицированным, если по оценкам коэффициентов приведённой формы системы одновременных уравнений можно получить более одного значения для коэффициентов структурной формы системы одновременных уравнений.
Исходная система одновременных уравнений называется неидентифицированной, если среди уравнений системы есть хотя бы одно неидентифицированное.
Уравнение называется неидентифицированным, если по оценкам коэффициентов приведённой формы системы одновременных уравнений невозможно рассчитать оценки коэффициентов структурной формы системы одновременных уравнений.
Одновременные уравнения. Методы идентификации
7.3. Структурная и приведенная формы системы одновременных уравнений
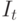
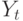
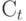
В кейнсианской модели (7.1) переменная и переменные и существенно различаются. Первая переменная формируется под воздействием внешних факторов, большинство из которых относится к политической надстройке, создающей условия для роста инвестиций, и называется экзогенной переменной. Остальные переменные модели определяются из уравнений (7.1), т.е. внутри модели, и называются эндогенными переменными.
Если система уравнений помимо экзогенных и эндогенных переменных содержит еще и значения эндогенных переменных, полученные в предыдущие периоды времени, то такие значения называют лаговыми переменными, или предопределенными переменными. Тогда в приведенной форме системы следует выражать эндогенные переменные через экзогенные и лаговые переменные.
Модернизируем кейнсианскую модель, предполагая, что даже при сильных изменениях совокупного продукта обществу будет трудно сразу приспособиться к новому уровню потребления и большую роль при этом будет играть сложившийся в прошлые периоды стереотип потребления. То есть предположим, что функция потребления имеет вид
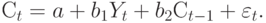| (7.5) |
В рассматриваемый период времени уровень потребления в прошлый период времени считается известным, поэтому переменная является предопределенной. Приведенная форма модернизированной кейнсианской модели будет содержать в правой части переменные и .
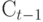
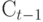
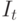
7.4. Косвенный и двухшаговый методы наименьших квадратов и проблема идентифицируемости
Метод, с помощью которого мы выше определили неизвестные структурные коэффициенты модели, называется косвенным методом наименьших квадратов. Суть его состоит в том, что сначала систему структурных уравнений преобразуют к приведенной форме. Затем коэффициенты приведенной формы рассчитывают по методу наименьших квадратов, и наконец, находят структурные коэффициенты из соотношений, связывающих приведенные и структурные коэффициенты уравнений.
Запишем приведенную систему уравнений (7.3) в несколько ином виде
9.3. проблемы идентифицируемости
9.3. проблемы идентифицируемости
В рассмотренном примере уравнения (9.6) были однозначно разрешимы относительно исходных параметров, что позволило найти их состоятельные оценки. Очевидно, что такая ситуация имеет место не всегда. Рассмотрим эту проблему более подробно.
Форма (9.2) называется структурной формой системы уравнений. В случае двух уравнений с двумя неизвестными структурной формой будем называть также уравнения (9.3)—(9.4). Параметры структурной формы называются структурными параметрами. Форма (9.5) называется приведенной формой системы. Параметры приведенной формы оцениваются с помощью метода наименьших квадратов. Однако экономический смысл и интерес для анализа представляют параметры структурной формы. Именно структурная форма раскрывает экономический механизм формирования значений эндогенных переменных.
Структурный параметр называется идентифицируемым, если он может быть однозначно оценен с помощью косвенного метода наименьших квадратов.
Уравнение идентифицируемо, если идентифицируемы все входящие в него структурные параметры.
Структурный параметр называется не идентифицируемым, если его значение невозможно получить, даже зная точные значения параметров приведенной формы. Наконец, параметр называется сверхидентифицируемым, если косвенный метод наименьших квадратов дает несколько различных его оценок.
Пусть, например, в рассматриваемой модели мы предполагаем, что переменная Y зависит от двух экзогенных переменных Х, Х>, между тем как динамика >2 определяется только эндогенной переменной Уі, т. е. система уравнений имеет вид:
Очевидно, что три коэффициента (Зь fori не могут быть найдены из двух уравнений (9.14). Это означает, что существует бесконечное множество их возможных значений, приводящих к одной и той же приведенной форме. Такие коэффициенты называются неидентифицируемылш и, соответственно, неидентифици-руемым называется уравнение, содержащее эти параметры.
В то же время для определения у2 мы имеем две различные возможности, задаваемые соотношением (9.15). При этом заметим, что необходимо выполнение равенства
Но хотя это равенство выполняется для истинных (неизвестных) значений параметров с и Ъ, для их оценок оно, конечно, выполняться не будет.
В качестве примера рассмотрим модель (9.12) с данными из примера 1 (см. § 9.2). Оценки параметров приведенной модели имеют значения (9.10).
Параметр, для которого существует несколько способов выражения через коэффициенты приведенной формы, называется сверхидентифицируемым. Таковым является параметр 72 из рассматриваемого примера. Для сверхидентифицируемого параметра имеется несколько, вообще говоря, различных оценок.
Заметим, что проблема сверхидентифицируемости — это проблема количества наблюдений: с увеличением объема выборки все различные состоятельные оценки параметра стремятся к одному и тому же истинному значению. Между тем проблема неидентифицируемости — это проблема структуры модели. Неидентифицируемость не исчезает с ростом количества наблюдений и означает, что существует бесконечное число структурных моделей, имеющих одну и ту же приведенную форму.
Неидентифицируемость вовсе не является редким явлением. В самом деле для идентифицируемости, грубо говоря, надо, чтобы количество оцениваемых структурных параметров было бы равно количеству оцененных параметров приведенной формы. Очевидно, однако, что в общем случае структурных параметров больше.
Очевидно, неидентифицируемость модели означает, что косвенный метод наименьших квадратов неприменим. В после дующих параграфах мы рассмотрим другие методы оценивания систем одновременных уравнений.