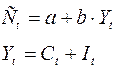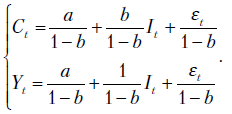структурный параметр называется идентифицируемым если
Структурный параметр называется идентифицируемым если
Добро пожаловать!
Теперь вы можете поделиться своей работой!
Просто нажмите на значок
ФЭУ / Экономика предприятий / лекция Проблемы идентифицируемости
Параметры структурной формы называют структурными параметрами.
Параметры приведенной формы называют приведенными параметрами.
Параметры приведенной формы оцениваются с помощью метода наименьших квадратов. Однако экономический смысл и интерес для анализа представляют параметры структурной формы. Именно структурная форма раскрывает экономический механизм формирования значений эндогенных переменных.
Проблемы идентифицируемости
Структурный параметр называется идентифицируемым, если он может однозначно оценен с помощью косвенного метода наименьших квадратов.
Уравнение идентифицируемо, если идентифицируемы все входящие в него структурные параметры.
Структурный параметр называется неидентифицируемым, если его значение невозможно получить, даже зная точные значения параметров приведенной формы.
Параметр называется сверхидентифицируемым, если косвенный метод наименьших квадратов дает несколько различных его оценок.
Проблема сверхидентифицируемости – это проблема количества наблюдений: с увеличением объема выборки все различные состоятельные оценки параметра стремятся к одному и тому же истинному значению.
Проблема неидентифицируемости – это проблема структуры модели.
Неидентифицируемость не исчезает с ростом количества наблюдений и означает, что существует бесконечное число структурных моделей, имеющих одну и ту же приведенную форму.
Неидентифицируемость не является редким явлением. Для идентифицируемости необходимо, чтобы количество оцениваемых структурных параметров было бы равно количеству оцененных параметров приведенной формы. Однако, в общем случае структурных параметров больше.
Неидентифицируемость модели означает, что косвенный метод наименьших квадратов неприменим.
Рассмотрим другие методы оценивания систем одновременных уравнений.
Метод инструментальных переменных.
Метод инструментальных переменных – один из наиболее распространенных методов оценивания уравнений, в которых регрессоры коррелируют со свободными членами. Именно это явление оказывается характерным для систем одновременных уравнений.
Идея метода заключается в подборе новых переменных, которые бы тесно коррелировали с экзогенными переменными и не коррелировали со случайной составляющей модели. Набор новых переменных может включать те регрессоры, которые не коррелируют со случайной составляющей, а также другие величины. Количество переменных может отличаться от исходного количества регрессоров. Такие переменные называются инструментальными. Они позволяют построить состоятельную оценку параметров модели.
Рассмотрим отдельно два случая – для идентифицируемой и неидентифицируемой системы.
Система идентифицируема. Если при оценке идентифицируемого уравнения в качестве инструментальных переменных используются экзогенные переменные, то получаемые при этом оценки совпадают с оценками косвенного метода наименьших квадратов.
Из этого следует, что косвенный метод наименьших квадратов является частным случаем метода инструментальных переменных.
На практике метод инструментальных переменных применяется в форме двухшагового метода наименьших квадратов. В качестве инструментальных переменных используются объясненные (прогнозные) значения эндогенных переменных, полученные при оценивании приведенной формы. Затем эти значения подставляются в правую часть структурной формы.
Если система идентифицируема, и количество экзогенных переменных Х совпадает с количеством эндогенных переменных Y, оценки двухшагового метода совпадают с оценками косвенного метода наименьших квадратов.
Система неидентифицируема.
В этом случае метод инструментальных переменных, вообще говоря, тоже применим, однако для его использования необходимо располагать «внешними» инструментальными переменными – экзогенных переменных не хватает.
Замену в структурной форме системы Yi на Ŷi иногда называют «очищением» эндогенной переменной. При этом удаляется та часть переменной, которая коррелирует с ошибками регрессии.
Одновременное оценивание регрессионных уравнений. Внешне не связанные уравнения.
Косвенный метод наименьших квадратов по сути сводится к оцениванию по отдельности уравнений приведенной формы.
Y1 = a1 + b1X1 + ν1
Y2 = a2 + b2X2 + ν2
Эффективность оценивания можно повысить, если объединить данные уравнения в одно и применить к нему обобщенный метод наименьших квадратов.
Для практического применения обобщенного метода наименьших квадратов следует оценить матрицу ∑. Это можно сделать, применив метод наименьших квадратов сначала к каждому из уравнений по отдельности, найти остатки регрессии и принять в качестве оценок матриц ∑ij выборочные ковариации. Очевидно, эти оценки будут состоятельными.
Применяя метод одновременного оценивания, можно повысить эффективность косвенного метода наименьших квадратов.
Если наборы экзогенных переменных в обоих уравнениях совпадают, то оценка одновременного оценивания совпадает с оценкой метода наименьших квадратов, примененного к уравнениям по отдельности.
Трехшаговый метод наименьших квадратов.
Наиболее эффективная процедура оценивания систем регрессионных уравнений сочетает метод одновременного оценивания и метод инструментальных переменных. Соответствующий метод называется трехшаговым методом наименьших квадратов.
Он заключается в том, что на первом шаге к исходной модели применяется обобщенный МНК с целью устранения корреляции случайных членов. Затем к полученным уравнениям применяется двухшаговый метод наименьших квадратов.
Если случайные члены не коррелируют, трехшаговый метод сводится к двухшаговому, в то же время, если матрица В – единичная, трехшаговый метод представляет собой процедуру одновременного оценивания уравнений как внешне не связанных.
Очищение уравнения от корреляции случайных членов – процесс итеративный. В соответствии с этим при использовании трехшагового метода компьютерная программа запрашивает число итераций или требуемую точность.
При достаточно большом числе итераций оценки трехшагового метода наименьших квадратов совпадают с оценками максимального правдоподобия, которые на больших выборках являются наилучшими.
Косвенный и двухшаговый метод наименьших квадратов и проблема идентифицируемости
Коэффициенты уравнений входящие в структурную систему уравнений можно разделить на две группы: подлежащие определению и заранее известные из исходных теоретических предположений о модели. В системе (7.1) первое уравнение системы содержит подлежащие определению структурные коэффициенты a и b, а второе – представляет тождество с заранее известными двумя коэффициентами равными единице.
Метод, с помощью которого мы определили неизвестные структурные коэффициенты модели в предыдущих пунктах главы, называется косвенным методом наименьших квадратов. Суть его состоит в том, что сначала система структурных уравнений преобразуется к приведенной форме. Затем коэффициенты приведенной формы рассчитываются по методу наименьших квадратов и, наконец, структурные коэффициенты находятся из соотношений связывающих приведенные и структурные коэффициенты уравнений.
Запишем приведенную систему уравнений (7.3) в несколько ином виде:
, (7.6)
где 
, 
, 
. Итак, существует, по крайней мере, два способа расчета коэффициентов a и b. Первый способ состоит в использовании для расчета коэффициентов 
и 
:
; 
. (7.7)
Несколько иные коэффициенты мы получим, если используем для расчетов формулы:
; 
. (7.8)
И хотя расчеты по формулам (7.7) и (7.8) могут случайно дать одинаковый результат, но в общем случае косвенный метод наименьших квадратов дает для простейшей кейнсианской модели (7.1) несколько вариантов расчета структурных коэффициентов модели. Такая ситуация называется ситуацией сверхидентифицируемости. Приведем соответствующие определения.
Структурный параметр (коэффициент структурного уравнения системы) называется идентифицируемым, если он однозначно определяется с помощью косвенного метода наименьших квадратов, то есть существует единственная формула, связывающая этот коэффициент с коэффициентами приведенной формы.
Уравнение структурной системы называется идентифицируемым, если идентифицируемы все входящие в него структурные коэффициенты.
Структурный параметр называется неидентифицируемым, если не существует формул расчета этого коэффициента через коэффициенты приведенной формы модели.
Структурный параметр называется сверхидентифицируемым, если существует несколько формул расчета этого коэффициента через коэффициенты приведенной формы модели.
Однозначный метод определения коэффициентов структурной модели в случае сверх идентифицируемости дает двухшаговый метод наименьших квадратов. Он состоит из следующих этапов:
1. Как и в случае косвенного метода наименьших квадратов на первом этапе находятся МНК-оценки коэффициентов приведенной формы.
2. Получают из уравнений приведенной формы расчетные значения эндогенных переменных.
3. Расчетные значения эндогенных переменных полученные на этапе 2 используют в качестве инструментальных переменных, то есть подставляют расчетные значения эндогенных переменных вместо их истинных значений в правые части структурных уравнений модели.
4. Снова используют МНК для расчета теперь уже структурных коэффициентов модели.
Для простейшей кейнсианской модели (7.1) двухшаговый МНК означает:
1. Расчет по методу наименьших квадратов коэффициентов 
, , 
системы (7.6).
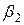
2. Определение расчетных значений 
и 
для каждого наблюдения t из уравнений системы (7.6).
3. Расчет оценок структурных коэффициентов a и b по методу наименьших квадратов из системы уравнений:
7.5. Контрольные вопросы и упражнения к главе 7.
1. Какие трудности при применении МНК возникают, если уравнение содержит случайные объясняющие переменные?
2. Какие переменные называются инструментальными и какова их роль в преодолении трудностей применения обычного МНК для построения регрессии?
3. Какие переменные системы уравнений называются экзогенными, эндогенными и предопределенными?
4. Какую форму системы уравнений называют структурной формой, а какую приведенной формой системы?
5. Получите в явном виде приведенную форму кейнсианской модели с модернизированным по Брауну процессом формирования потребления в экономической системе (см. (7.5)).
6. Какие структурные коэффициенты модели называются идентифицированными, неидентифицируемыми, сверхидентифицируемыми?
7. Когда можно использовать для получения оценок структурной модели косвенный метод наименьших квадратов, а когда двухшаговый метод наименьших квадратов?
Структурный параметр называется идентифицируемым если
Структурный параметр называется идентифицируемым, если он может быть однозначно оценен с помощью косвенного метода наименьших квадратов. [c.231]
Уравнение идентифицируемо, если идентифицируемы все входящие в него структурные параметры. [c.231]
Иначе говоря, проблема идентифицируемости структурных параметров — это проблема достаточности эмпирических данных для оценки всех коэффициентов модели. Необходимым условием идентифицируемости уравнения является отсутствие среди линейных комбинаций оставшихся уравнений, таких, которые удовлетворяли бы всем ограничениям модели, накладываемым на исследуемое уравнение. [c.220]
Из теоремы 1 следует, что структурные параметры (Во, Го, HO) идентифицируемы тогда и только тогда, когда их значения могут быть выведены из параметров приведенной формы (П0, о)- Поскольку без априорных ограниче- [c.417]
С проблемой идентификации модели не следует путать проблему ее идентифицируемости (гл. 9), т. е. проблему возможности получения однозначно определенных параметров модели, заданной системой одновременных уравнений (точнее, параметров структурной формы модели, раскрывающей механизм формирования значений эндогенных переменных, по параметрам приведенной формы модели, в которой эндогенные переменные непосредственно выражаются через предопределенные переменные). [c.22]
Модель идентифицируема, если все структурные ее коэффициенты определяются однозначно, единственным образом по коэффициентам приведенной формы модели, т. е. если число параметров структурной модели равно числу параметров приведенной формы модели. В этом случае структурные коэффициенты модели оцениваются через параметры приведенной формы модели и модель идентифицируема. Рассмотренная выше структурная модель (4.4) с двумя эндогенными и тремя экзогенными (предопределенными) переменными, содержащая шесть структурных коэффициентов, представляет собой идентифицируемую модель. [c.187]
Для оценки параметров структурной модели система должна быть идентифицируема или сверхидентифицируема. [c.189]
Рассмотренное счетное правило отражает необходимое, но недостаточное условие идентификации. Более точно условия идентификации определяются, если накладывать ограничения на коэффициенты матриц параметров структурной модели. Уравнение идентифицируемо, если по отсутствующим в нем переменным (эндогенным и экзогенным) можно из коэффициентов при них в других уравнениях системы получить матрицу, оп- [c.189]
Кроме того, существуют также чисто технические причины для соблюдения осторожности при оценке всех выводов, рассмотренных в разделах 20.1 и 20.2. Самая важная из них заключается в том, что в упомянутых исследованиях использовались такие приемы, как, например, обычная регрессия, рассчитываемая по методу наименьших квадратов, которые не учитывают, что функция спроса на деньги-это лишь одно структурное уравнение внутри целой системы одновременно решаемых уравнений. Это порождает и другие проблемы. Одна из них-это проблема идентификации. Без спецификации функций предложения денег и других уравнений системы невозможно выяснить, идентифицируема ли функция спроса на деньги. Лишь в том случае, когда другие уравнения обладают определенными свойствами, можно получить ответ, выводятся ли расчетные параметры функции спроса из данных, полученных в точке пересечения устойчивой функции подлинного спроса со смещающейся функцией предложения, или смещается сама функция спроса. Только при наличии первой ситуации можно быть уверенным, что эмпирически обнаруживаемая связь между денежным запасом и группой независимых переменных представляет собой эмпирическую функцию спроса. Другой проблемой является ошибка одновременно решаемой системы уравнений. Чтобы решить проблему идентификации, достаточно дать спецификацию других структурных уравнений, убедиться, что эта процедура проделана правильно, и исследовать свойства модели. Но даже если модель такова, что [c.648]
Неидентифицируемость вовсе не является редким явлением. В самом деле для идентифицируемости, грубо говоря, надо, чтобы количество оцениваемых структурных параметров было бы равно количеству оцененных параметров приведенной формы. Очевидно, однако, что в общем случае структурных параметров больше. [c.232]
В более общем случае, когда модель состоит из одновременных уравнений, не удовлетворяющих специальным предположениям о рекур-сивности, существует простой метод оценивания — косвенный метод наименьших квадратов, но он применим лишь к точно идентифицируемым уравнениям. Состоит этот метод в использовании обыкновенного метода наименьших квадратов для оценивания параметров каждого из уравнений структурной формы в отдельности и в последующем выводе оценок структурных параметров с помощью преобразования ВП = —Г, где вместо матрицы П берется матрица оценок параметров приведенной формы П. Элементы матрицы П будут наилучшими линейными несмещенными оценками, однако это свойство не сохраняется при преобразованиях, и полученные оценки структурных параметров, по-видимому, окажутся смещенными. Тем не менее и оценки П, и оценки косвенного метода наименьших квадратов будут состоятельными. Для [c.375]
Переменные R и экзогенные. Введя их в модель, получим идентифицируемую структурную модель, оценки параметров которой могут быть даны с помощью КМНК. [c.211]
Одновременные уравнения. Методы идентификации
7.3. Структурная и приведенная формы системы одновременных уравнений
В кейнсианской модели (7.1) переменная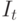 
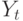
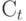
и переменные 
и 
существенно различаются. Первая переменная формируется под воздействием внешних факторов, большинство из которых относится к политической надстройке, создающей условия для роста инвестиций, и называется экзогенной переменной. Остальные переменные модели определяются из уравнений (7.1), т.е. внутри модели, и называются эндогенными переменными.
Если система уравнений помимо экзогенных и эндогенных переменных содержит еще и значения эндогенных переменных, полученные в предыдущие периоды времени, то такие значения называют лаговыми переменными, или предопределенными переменными. Тогда в приведенной форме системы следует выражать эндогенные переменные через экзогенные и лаговые переменные.
Модернизируем кейнсианскую модель, предполагая, что даже при сильных изменениях совокупного продукта обществу будет трудно сразу приспособиться к новому уровню потребления и большую роль при этом будет играть сложившийся в прошлые периоды стереотип потребления. То есть предположим, что функция потребления имеет вид
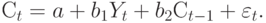 | (7.5) |
В рассматриваемый период времени 
уровень потребления в прошлый период времени считается известным, поэтому переменная 
является предопределенной. Приведенная форма модернизированной кейнсианской модели будет содержать в правой части переменные и .
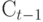
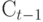
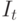
7.4. Косвенный и двухшаговый методы наименьших квадратов и проблема идентифицируемости
Метод, с помощью которого мы выше определили неизвестные структурные коэффициенты модели, называется косвенным методом наименьших квадратов. Суть его состоит в том, что сначала систему структурных уравнений преобразуют к приведенной форме. Затем коэффициенты приведенной формы рассчитывают по методу наименьших квадратов, и наконец, находят структурные коэффициенты из соотношений, связывающих приведенные и структурные коэффициенты уравнений.
Запишем приведенную систему уравнений (7.3) в несколько ином виде
Одновременные уравнения. Методы идентификации
7.3. Структурная и приведенная формы системы одновременных уравнений
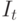
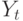
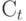
В кейнсианской модели (7.1) переменная и переменные и существенно различаются. Первая переменная формируется под воздействием внешних факторов, большинство из которых относится к политической надстройке, создающей условия для роста инвестиций, и называется экзогенной переменной. Остальные переменные модели определяются из уравнений (7.1), т.е. внутри модели, и называются эндогенными переменными.
Если система уравнений помимо экзогенных и эндогенных переменных содержит еще и значения эндогенных переменных, полученные в предыдущие периоды времени, то такие значения называют лаговыми переменными, или предопределенными переменными. Тогда в приведенной форме системы следует выражать эндогенные переменные через экзогенные и лаговые переменные.
Модернизируем кейнсианскую модель, предполагая, что даже при сильных изменениях совокупного продукта обществу будет трудно сразу приспособиться к новому уровню потребления и большую роль при этом будет играть сложившийся в прошлые периоды стереотип потребления. То есть предположим, что функция потребления имеет вид
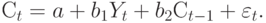| (7.5) |
В рассматриваемый период времени уровень потребления в прошлый период времени считается известным, поэтому переменная является предопределенной. Приведенная форма модернизированной кейнсианской модели будет содержать в правой части переменные и .
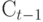
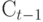
7.4. Косвенный и двухшаговый методы наименьших квадратов и проблема идентифицируемости
Метод, с помощью которого мы выше определили неизвестные структурные коэффициенты модели, называется косвенным методом наименьших квадратов. Суть его состоит в том, что сначала систему структурных уравнений преобразуют к приведенной форме. Затем коэффициенты приведенной формы рассчитывают по методу наименьших квадратов, и наконец, находят структурные коэффициенты из соотношений, связывающих приведенные и структурные коэффициенты уравнений.
Запишем приведенную систему уравнений (7.3) в несколько ином виде