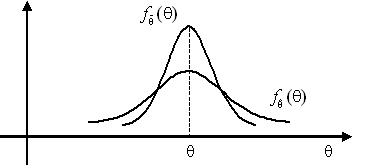
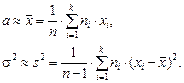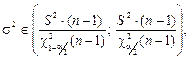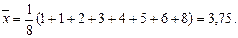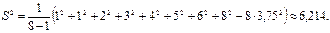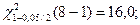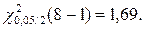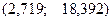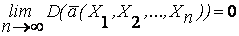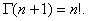точечная оценка математическое ожидание которой равно оцениваемому параметру называется

Точечная оценка параметров распределения

Тема 7. Статистические оценки параметров распределения: точечные и интервальные оценки

Смысл статистических методов заключается в том, чтобы по выборке ограниченного объема, то есть по некоторой части генеральной совокупности, высказать обоснованное суждение о ее свойствах целиком.

Естественно, что замена исследования генеральной совокупно­сти исследованием выборки порождает ряд вопросов:

1. В какой степени выборка отражает свойства генеральной совокупности, т. е. в какой степени выборка репрезентативна по отношению к генеральной совокупности?

2. Какую информацию о значениях параметров генеральной совокупности могут дать параметры выборки?

3. Можно ли утверждать, что полученные выборочным путем статистические характеристики (средние величины, дисперсия или любые другие производные величины) равны тем характе­ристикам, которые могут быть получены из генеральной сово­купности.

Проверка показывает, что значения параметров, полученных для разных выборок из одной генеральной совокупности, обыч­но не совпадают. Рассчитанные выборочным путем числовые значения параметров выборок являются лишь результатом при­ближенного статистического оценивания значений этих парамет­ров в генеральной совокупности. Статистическое оценивание, в силу изменчивости наблюдаемых явлений, позволяет получать только их приближенные значения.

Примечание. Строго говоря, в статистике оценка — это правило вычисления оцениваемого параметра, а термин оценить, т. е. провести оценивание, означает указать приближенное значе­ние.

Различают оценки точечные и оценки интервальные.

Точечная оценка параметров распределения

Пусть x₁, x₂, …, x_n – выборка объема n из генеральной совокупности с функцией распределения F(x).

Числовые характеристики этой выборки называются выборочными (эмпирическими) числовыми характеристиками.

Отметим, что выборочные числовые характеристики являются характеристиками данной выборки, но не являются характеристиками распределения генеральной совокупности. Однако эти характеристики можно использовать для оценок параметров генеральной совокупности.

Точечной называют статистическую оценку, которая определяется одним числом.

Точечная оценка характеризуется свойствами:несмещенность, состоятельность и эффективность.

Несмещенной называют точечную оценку, математическое ожидание которой равно оцениваемому параметру при любом объеме выборки.

Точечная оценка называется состоятельной, если при неограниченном увеличении объема выборки (n ® ¥) она сходится по вероятности к истинному значению параметра, то есть стремится к истинному значению оцениваемого параметра генеральной совокупности.

Эффективной называют точечную оценку, которая (при заданном объеме выборки n) имеет наименьшую возможную дисперсию, те есть гарантирует наименьшее отклонение выборочной оценки от такой же оценки генеральной совокупности..

В математической статистике показывается, что состоятельной, несмещенной оценкой генерального среднего значения а является выборочное средне:

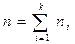
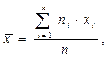
где х_i – варианта выборки, n_i – частота варианты х_i, – объем выборки.

Несмещенной оценкой генеральной дисперсии служит исправления выборочная дисперсия

,

Более удобна формула .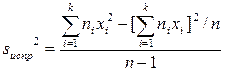

Оценка s 2 для генеральной дисперсии является также и состоятельной, но не является эффективной. Однако в случае нормального распределения она является «асимптотически эффективной», то есть при увеличении n отношение ее дисперсии к минимально возможной неограниченно приближается к единице.

Точечные оценки имеют тот недостаток, что при малом объеме выборки могут значительно отличаться от оцениваемых параметров. Поэтому, чтобы получить представление о близости между параметром и его оценкой, в математической статистике вводятся, так называемые, интервальные оценки.

Доверительный интервал

Если при статистической обработке результатов требуется найти не только точечную оценку неизвестного параметра θ, но и охарактеризовать точность этой оценки, то находится доверительный интервал.

Доверительный интервал – это интервал, в котором заранее заданной доверительной вероятностью находится неизвестный параметр генеральной совокупности.

Доверительная вероятность – это вероятность, с которой неизвестный параметр генеральной совокупности принадлежит доверительному интервалу.

Обычно принимают р = 0,95 или (реже) 0,99. Эти вероятности признаны достаточными для уверенного суждения о генеральных параметрах на основании известных выборочных показателей.

Доверительный интервал для математического ожидания имеет вид: где S – СКО, — критическое значение распределения Стьюдента (Смотри ПРИЛОЖЕНИЕ 1 к Теме 7)

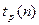
Доверительный интервал для дисперсии имеет вид

где 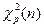— обратное распределение хи-квадрат (Смотри ПРИЛОЖЕНИЕ 2 к Теме 7)

ЗАДАЧА. Дана выборка 5, 6, 8, 2, 3, 1, 1, 4. Записать данные в виде вариационного ряда. Определить оценки среднего, дисперсии, и стандартного отклонения а также построить доверительные интервалы для среднего и дисперсии на уровне значимости a=0,05.

Решение. Представим данные в виде вариационного ряда: 1, 1, 2, 3, 4, 5, 6, 8. Так как n = 8, то выборочное среднее и исправленная выборочная дисперсия равны

Стандартное отклонение .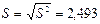

По таблицам из ПРИЛОЖЕНИЯ 1 и ПРИЛОЖЕНИЯ 2 к Теме 7. находим: ,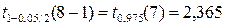

Получаем доверительный интервал для математического ожидания

или .

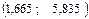
Доверительный интервал для дисперсии

или

Источник

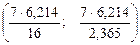
Математическая статистика

Точечные оценки

Свойства точечных оценок

Пусть x₁. x_n – выборка наблюдений случайной величины X, имеющей распределение F_X(x). При проведении ряда статистических исследований вид функции распределения наблюдаемой случайной величины зачастую предполагается известным (например, случайная величина имеет нормальное или биномиальное распределение). Неизвестными же являются параметры этого распределения.

Одной из задач математической статистики является оценка неизвестных параметров распределения наблюдаемой случайной величины X по выборке x₁. x_n её наблюдений.

Параметром θ∈Θ распределения F_X(x) случайной величины X называется любая числовая характеристика этой случайной величины (математическое ожидание, дисперсия и т.п.) или любая константа, явно входящая в выражение для функции распределения F_X(x).

Напомним, что любая выборка наблюдений x₁. x_n является реализацией случайной выборки X₁. X_n. Статистикой Z в математической статистике называется произвольная функция случайной выборки, не зависящая от неизвестных параметров распределения:

В связи с тем, что статистика Z является функцией случайных аргументов, Z является случайной величиной. Для каждой реализации x₁. x_n случайной выборки X₁. X_n получим соответствующую ей реализацию z статистики Z:

называемую выборочным значением статистики Z.

Основные свойства точечных оценок.

1. Состоятельность (Consistency)

$\forall \varepsilon >0\ \ \ P\left( \left| <<<\tilde<\theta >>>_>-\theta \right|\ge \varepsilon \right)\to 0$,

3. Эффективность (Efficiency)

Для оценки параметра θ может быть предложено несколько несмещённых оценок. Вследствие несмещённости различные реализации этих оценок будут группироваться относительно их математического ожидания, равного θ, однако разброс этих значений может быть различным. Как известно, мерой разброса значений случайной величины относительно математического ожидания является её дисперсия.

Оценка параметра θ, имеющая минимально возможную дисперсию среди всех оценок, называется эффективной оценкой параметра θ. В математической статистике наряду с термином «эффективная оценка» используют и другие: «несмещённая оценка с минимальной дисперсией», «оптимальная оценка».

При выполнении условий регулярности каждый элемент независимой случайной выборки X₁. X_n вносит равный вклад в информацию Фишера I_n(θ), т.е.

где I(θ) – количество информации по Фишеру о параметре θ, содержащееся в одном выборочном наблюдении.

Величина информации по Фишеру зависит от вида распределения генеральной совокупности X. Так, выборки, полученные из генеральных совокупностей с разными распределениями (например, нормальным и биномиальным) будут содержать различное количество информации о неизвестных математическом ожидании или дисперсии.

Чем больше информации по Фишеру о параметре θ содержится в выборочных наблюдениях, тем меньший разброс имеют реализации эффективной оценки этого параметра, а следовательно, являются более точными.

Формально информация по Фишеру о параметре θ, содержащаяся в одном выборочном наблюдении из генеральной совокупности с функцией плотности распределения f_X(x, θ), рассчитывается по формуле

называется вкладом выборки.

Источник

Математическая статистика

Точечные оценки

Точечные оценки математического ожидания и дисперсии

1. Оценки математического ожидания

1) Оптимальной оценкой математического ожидания является выборочное среднее

Оценка является несмещённой, состоятельной, эффективной.

2) На практике нередко возникает необходимость быстрой оценки математического ожидания. Такой оценкой может быть

Оценка является состоятельной и, по крайней мере, асимптотически несмещённой и асимптотически эффективной.

3) В качестве оценки математического ожидания симметричного распределения может быть использована выборочная медиана

Оценка является состоятельной, несмещённой, но неэффективной.

является несмещённой, состоятельной, эффективной.

2. Оценки дисперсии

1) Оптимальной оценкой дисперсии является исправленная выборочная дисперсия:

Оценка является несмещённой, состоятельной, эффективной.

2) Выборочная дисперсия

Оценка является асимптотически несмещённой, состоятельной, асимптотически эффективной.

3) На практике нередко возникает необходимость быстрой оценки дисперсии. Такой оценкой может быть

Оценка является грубой, для большинства распределений смещённой и неэффективной.

4) В случае если известно математическое ожидание m генеральной совокупности, оптимальной оценкой дисперсии является статистика:

Оценка является несмещённой, состоятельной, эффективной.

является несмещённой, состоятельной, эффективной.

Источник

Точечная оценка математического ожидания

Задана случайная величина Х: х₁, х₂, …, х_n, так как М(Х) не найти, то для математического ожидания случайной величины Х естественно предложить среднее арифметическое

(1.3)

её наблюденных значений.

1. По методу произведений

, ,

.

Это и означает, что оценка несмещенная.

2. Если исследуемая случайная величина Х имеет конечную дисперсию, то эта оценка будет состоятельной, так как

.

Если исследуемая величина имеет нормальный закон распределения, то можно показать, что предложенная оценка эффективна, т. е. оценки для математического ожидания с меньшей дисперсией не существует для нормально распределенных величин

,

а .

Так как параметр генеральной совокупности оценивается числом, которое на числовой оси изображается точкой, то оценку называют точечной.

Для того чтобы оценка имела практическую ценность она должна обладать следующими свойствами.

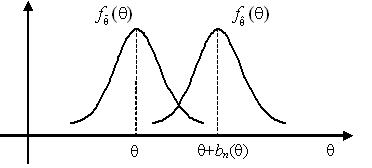
1. Несмещенность оценки. Оценка называется несмещенной, если ее математическое ожидание равно оцениваемому параметру генеральной совокупности:

В противном случае оценка называется смещенной и допускает систематическую ошибку.

2. Состоятельность оценки. Оценка называется состоятельной, если она по вероятности с увеличением объема выборки п стремится к параметру генеральной совокупности:

Это условие будет выполняться, если

и оценка является несмещенной. Доказательство этого основано на неравенстве Чебышева.

3. Эффективность оценки. Если составлять множество несмещенных и состоятельных оценок, то эти оценки будут иметь разные дисперсии. Ясно, что, чем меньше будет дисперсия, тем меньше будет вероятность грубой ошибки при определении приближенного параметра генеральной совокупности. Поэтому нужно выбрать такую оценку, у которой дисперсия была бы минимальной:

Такая оценка называется эффективной.

Выборочная дисперсия характеризует разброс (рассеивание) значений вариант хi от выборочного среднего значения х_в и измеряется в квадратных единицах измерения признака Х

Св-ва: Выборочные дисперсии Dв и S 2 являются состоятельными

оценками для генеральной дисперсии

, ,( ) (8.2)

Для равномерного распределения имеем теоретические моменты

, .

Прировняем теоретические моменты выборочным и получаем систему двух уравнений с двумя неизвестными для нахождения оценок параметров а1, а2:

Решая эту систему, получаем в окончательном виде

, ,

где величины , определены соотношениями (2)

.

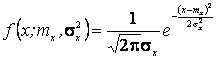
Решение. Так как первый начальный момент нормального распределения равен параметру тх., а второй центральный момент равен параметру ,

, .

Пример. Пусть Х – непрерывная случайная величина подчинена показательному (экспоненциальному) закону, плотность распределения которого зависит от одного неизвестного параметра :

, х 0.

= = .

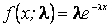
Отсюда получаем оценку параметра :

.▄

9. Использование метода моментов для получения параметров биномиального распределения и геометрического распределения

Метод моментовоснован на приравнивании моментов (центральных, начальных) СВ X к их выборочным оценкам. При этом число составляемых уравнений равно числу неизвестных параметров.

Пример. Пусть Х

Согласно этому методу нужно вычислить два момента (начальный 1-го порядка и центральный 2-го порядка) СВ X: m_X = (a+b)/2 и D_X = (b-a) 2 /12 и составить два уравнения (1) и (2), приравнивая моменты (A+B)/2 и (B-A) 2 /12 к их соответствующим выборочным значениям

и . Следовательно:

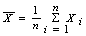
10 Основные распределения, используемые в математической статистике:

распределение хи- квадрат. Примеры использования распределения

Нормальное распределение играет исключительно важную роль в математической статистике. Такое распределение наиболее часто встречается на практике. Главная особенность, выделяющая нормальное распределение среди других распределений, состоит в том, что оно является предельным, к которому приближаются остальные распределения при весьма часто встречающихся типичных условиях.

Распределение случайной величины называется нормальным, если это распределение характеризуется плотностью следующего вида

где математическое ожидание , а среднеквадратическое отклонение ( дисперсия). Таким образом, мы видим, что нормальное распределение описывается двумя параметрами и .

Замечание 1. Общим называют нормальное распределение с произвольными параметрами и . Замечание 1*. Нормированной называют нормальное распределение с параметрами и
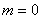
Замечание 2. Генеральная совокупность называется нормальной, если она распределена нормально.

Распределение основных статистик, которые вычисляются по выборке из нормально распределенной генеральной совокупности, связаны с распределением “хи-квадрат” и Стьюдента .

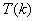
Распределением с степенями свободы называется распределение случайной величины , равной сумме квадратов независимых нормально распределенных по закону случайных величин , то есть величины

Плотность этого распределения

где – гамма функция; в частности,

Отсюда видно, что распределение “хи квадрат” определяется одним параметром – числом степеней свободы .

Замечание 3. С увеличением числа степеней свободы распределение медленно приближается к нормальному.

Распределением Стьюдента с степенями свободы называется распределение случайной величины , равной отношению двух независимых случайных величин и , то есть

,

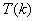
где имеет нормальное распределение .

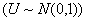
Замечание 4. С возрастанием числа степеней свободы распределение Стьюдента быстро приближается к нормальному распределению.

Источник