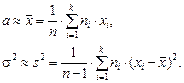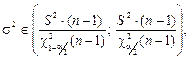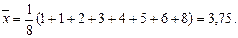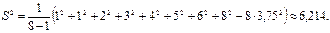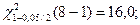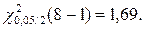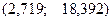точечная оценка неизвестного параметра

Статистическое оценивание

Материал из MachineLearning.

Содержание

Постановка задачи

Различают два основных типа оценок: точечные оценки и доверительные интервалы.

Точечное оценивание

К общим методам построения точечных оценок параметров относятся: метод максимального правдоподобия, метод моментов, метод квантилей.

Ниже приводятся некоторые свойства, которыми могут обладать или не обладать точечные оценки.

Состоятельность

Когда употребляют просто термин состоятельность, то обычно имеется в виду слабая состоятельность, т.е. сходимость по вероятности.

Условие состоятельности является практически обязательным для всех используемых на практике оценок. Несостоятельные оценки используются крайне редко.

Несмещенность и асимптотическая несмещенность

Оценка параметра называется несмещенной, если ее математическое ожидание равно истинному значению оцениваемого параметра:

Более слабым условием является асимптотическая несмещенность, которая означает, что математическое ожидание оценки сходится к истинному значению параметра с ростом объема выборки:

Сравнение оценок и эффективность

Для сравнения между собой различных оценок одного и того же параметра применяют следующий метод: выбирают некоторую функцию риска, которая измеряет отклонение оценки от истинного значения параметра, и лучшей считают ту, для которой эта функция принимает меньшее значение.

Чаще всего в качестве функции риска рассматривают математическое ожидание квадрата отклонения оценки от истинного значения

Существует нижняя граница на данную функцию риска, называемая неравенство Крамера-Рао.

(Несмещенные) оценки, для которых достигается эта нижняя граница (т.е. имеющие минимально возможную дисперсию), называются эффективными. Однако существование эффективной оценки есть довольно сильное требование на задачу, которое имеет место далеко не всегда.

Достаточные статистики

(Несмещенная) эффективная оценка параметра всегда является достаточной статистикой.

Доверительные интервалы

Другим типом оценок статистических параметров являются доверительные интервалы.

Доверительные интервалы используются, когда нам нужны надежные границы, в которые попадает значение оцениваемого параметра.

Часто вместе с точечной оценкой параметра строят доверительный интервал, середина которого равна этой оценке. Его ширина является наглядной характеристикой того, насколько точна может быть данная точечная оценка.

Иногда бывает наоборот: естественным образом строится некоторый доверительный интервал, а в качестве точечной оценки параметра рассматривают его середину.

Источник

Точечная оценка параметров распределения

Тема 7. Статистические оценки параметров распределения: точечные и интервальные оценки

Смысл статистических методов заключается в том, чтобы по выборке ограниченного объема, то есть по некоторой части генеральной совокупности, высказать обоснованное суждение о ее свойствах целиком.

Естественно, что замена исследования генеральной совокупно­сти исследованием выборки порождает ряд вопросов:

1. В какой степени выборка отражает свойства генеральной совокупности, т. е. в какой степени выборка репрезентативна по отношению к генеральной совокупности?

2. Какую информацию о значениях параметров генеральной совокупности могут дать параметры выборки?

3. Можно ли утверждать, что полученные выборочным путем статистические характеристики (средние величины, дисперсия или любые другие производные величины) равны тем характе­ристикам, которые могут быть получены из генеральной сово­купности.

Проверка показывает, что значения параметров, полученных для разных выборок из одной генеральной совокупности, обыч­но не совпадают. Рассчитанные выборочным путем числовые значения параметров выборок являются лишь результатом при­ближенного статистического оценивания значений этих парамет­ров в генеральной совокупности. Статистическое оценивание, в силу изменчивости наблюдаемых явлений, позволяет получать только их приближенные значения.

Примечание. Строго говоря, в статистике оценка — это правило вычисления оцениваемого параметра, а термин оценить, т. е. провести оценивание, означает указать приближенное значе­ние.

Различают оценки точечные и оценки интервальные.

Точечная оценка параметров распределения

Пусть x₁, x₂, …, x_n – выборка объема n из генеральной совокупности с функцией распределения F(x).

Числовые характеристики этой выборки называются выборочными (эмпирическими) числовыми характеристиками.

Отметим, что выборочные числовые характеристики являются характеристиками данной выборки, но не являются характеристиками распределения генеральной совокупности. Однако эти характеристики можно использовать для оценок параметров генеральной совокупности.

Точечной называют статистическую оценку, которая определяется одним числом.

Точечная оценка характеризуется свойствами:несмещенность, состоятельность и эффективность.

Несмещенной называют точечную оценку, математическое ожидание которой равно оцениваемому параметру при любом объеме выборки.

Точечная оценка называется состоятельной, если при неограниченном увеличении объема выборки (n ® ¥) она сходится по вероятности к истинному значению параметра, то есть стремится к истинному значению оцениваемого параметра генеральной совокупности.

Эффективной называют точечную оценку, которая (при заданном объеме выборки n) имеет наименьшую возможную дисперсию, те есть гарантирует наименьшее отклонение выборочной оценки от такой же оценки генеральной совокупности..

В математической статистике показывается, что состоятельной, несмещенной оценкой генерального среднего значения а является выборочное средне:

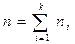
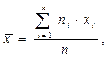
где х_i – варианта выборки, n_i – частота варианты х_i, – объем выборки.

Несмещенной оценкой генеральной дисперсии служит исправления выборочная дисперсия

,

Более удобна формула .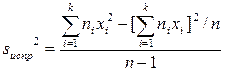

Оценка s 2 для генеральной дисперсии является также и состоятельной, но не является эффективной. Однако в случае нормального распределения она является «асимптотически эффективной», то есть при увеличении n отношение ее дисперсии к минимально возможной неограниченно приближается к единице.

Точечные оценки имеют тот недостаток, что при малом объеме выборки могут значительно отличаться от оцениваемых параметров. Поэтому, чтобы получить представление о близости между параметром и его оценкой, в математической статистике вводятся, так называемые, интервальные оценки.

Доверительный интервал

Если при статистической обработке результатов требуется найти не только точечную оценку неизвестного параметра θ, но и охарактеризовать точность этой оценки, то находится доверительный интервал.

Доверительный интервал – это интервал, в котором заранее заданной доверительной вероятностью находится неизвестный параметр генеральной совокупности.

Доверительная вероятность – это вероятность, с которой неизвестный параметр генеральной совокупности принадлежит доверительному интервалу.

Обычно принимают р = 0,95 или (реже) 0,99. Эти вероятности признаны достаточными для уверенного суждения о генеральных параметрах на основании известных выборочных показателей.

Доверительный интервал для математического ожидания имеет вид: где S – СКО, — критическое значение распределения Стьюдента (Смотри ПРИЛОЖЕНИЕ 1 к Теме 7)

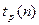
Доверительный интервал для дисперсии имеет вид

где 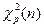— обратное распределение хи-квадрат (Смотри ПРИЛОЖЕНИЕ 2 к Теме 7)

ЗАДАЧА. Дана выборка 5, 6, 8, 2, 3, 1, 1, 4. Записать данные в виде вариационного ряда. Определить оценки среднего, дисперсии, и стандартного отклонения а также построить доверительные интервалы для среднего и дисперсии на уровне значимости a=0,05.

Решение. Представим данные в виде вариационного ряда: 1, 1, 2, 3, 4, 5, 6, 8. Так как n = 8, то выборочное среднее и исправленная выборочная дисперсия равны

Стандартное отклонение .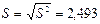

По таблицам из ПРИЛОЖЕНИЯ 1 и ПРИЛОЖЕНИЯ 2 к Теме 7. находим: ,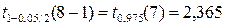

Получаем доверительный интервал для математического ожидания

или .

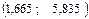
Доверительный интервал для дисперсии

или

Источник

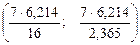
Статистическое оценивание

Материал из MachineLearning.

Содержание

Постановка задачи

Различают два основных типа оценок: точечные оценки и доверительные интервалы.

Точечное оценивание

К общим методам построения точечных оценок параметров относятся: метод максимального правдоподобия, метод моментов, метод квантилей.

Ниже приводятся некоторые свойства, которыми могут обладать или не обладать точечные оценки.

Состоятельность

Когда употребляют просто термин состоятельность, то обычно имеется в виду слабая состоятельность, т.е. сходимость по вероятности.

Условие состоятельности является практически обязательным для всех используемых на практике оценок. Несостоятельные оценки используются крайне редко.

Несмещенность и асимптотическая несмещенность

Оценка параметра называется несмещенной, если ее математическое ожидание равно истинному значению оцениваемого параметра:

Более слабым условием является асимптотическая несмещенность, которая означает, что математическое ожидание оценки сходится к истинному значению параметра с ростом объема выборки:

Сравнение оценок и эффективность

Для сравнения между собой различных оценок одного и того же параметра применяют следующий метод: выбирают некоторую функцию риска, которая измеряет отклонение оценки от истинного значения параметра, и лучшей считают ту, для которой эта функция принимает меньшее значение.

Чаще всего в качестве функции риска рассматривают математическое ожидание квадрата отклонения оценки от истинного значения

Существует нижняя граница на данную функцию риска, называемая неравенство Крамера-Рао.

(Несмещенные) оценки, для которых достигается эта нижняя граница (т.е. имеющие минимально возможную дисперсию), называются эффективными. Однако существование эффективной оценки есть довольно сильное требование на задачу, которое имеет место далеко не всегда.

Достаточные статистики

(Несмещенная) эффективная оценка параметра всегда является достаточной статистикой.

Доверительные интервалы

Другим типом оценок статистических параметров являются доверительные интервалы.

Доверительные интервалы используются, когда нам нужны надежные границы, в которые попадает значение оцениваемого параметра.

Часто вместе с точечной оценкой параметра строят доверительный интервал, середина которого равна этой оценке. Его ширина является наглядной характеристикой того, насколько точна может быть данная точечная оценка.

Иногда бывает наоборот: естественным образом строится некоторый доверительный интервал, а в качестве точечной оценки параметра рассматривают его середину.

Источник

СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЯ

ТОЧЕЧНЫЕ ОЦЕНКИ ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЯ

Одной из задач математической статистики является оценка неизвестных параметров закона распределения генеральной совокупности X. Вид закона распределения X может быть известным или неизвестным, и задача сводится к нахождению приближенных значений искомых параметров распределения или числовых характеристик X с использованием выборки из генеральной совокупности.

Определение. Точечной оценкой параметра 0 распределения генеральной совокупности ^называется статистика 0 (л) (Х (л) ), реализации которой 0 (л) (х (и) ) используются как приближенные значения этого параметра.

Наряду со статистикой 0 (л) (Х (л) ) точечной оценкой параметра 0 называют и функцию п переменных 0 (л) (х (л) ).

Качество оценки характеризуется следующими основными свойствами.

1. Несмещенность точечной оценки

Определение. Статистику 0 (л) (Х (и) ) называют несмещенной оценкой параметра 0 распределения генеральной совокупности X, если ее математическое ожидание совпадает с 0 для любого п е N:

При выполнении этого требования в пределе, т.е. когда

оценку 0 (/,) называют асимптотически несмещенной.

Пример 25.1. Доказать, что выборочные начальные моменты 1 п

? Найдем математическое ожидание статистики а_к(Х <п) ) = 1 «

Поскольку случайные величины X_t распределены по тому же закону, что и генеральная совокупность X, можно записать М[Х к = = М[Х к = а_к[Х]. Поэтому

оценки х величины т_х подставить саму эту величину, т.е. положить

Убедитесь, что выборочная дисперсия (25.2) является несмещенной оценкой дисперсии о 2 _х генеральной совокупности X.

Пример 25.3. Пусть статистика X = — X_t есть выборочное сред-

нее, см. (24.4). Покажите, что

где а (/l) ) из (24.6) как оценки дисперсии о 2 _х генеральной совокупности X.

Отсюда с учетом (25.3) получаем

т.е. Sq (х (я) ) — это смещенная оценка дисперсии о 2 _х генеральной совокупности X. Однако lim mSq (X (w) )1 = g 2 _x, что означает асимптоти-

1. Рассмотрим оценку iS’ 2 (x (w) ) = —— 5о(х (л) ), т.е.

Как уже отмечалось в п. 24.2, ее называют исправленной выборочной дисперсией. Из примера 25.4 следует, что М[5 2 (Х (/г) )] = 2 _х, т.е. 5 2 (х (я) ) есть несмещенная оценка дисперсии а 2 _х генеральной совокупности X.

2. Состоятельность точечной оценки

Определение. Статистику 0 ( ‘ г) (Х (/г) ) называют состоятельной оценкой параметра 0 распределения генеральной совокупности X, если с ростом объема выборки п она сходится по вероятности к этому параметру:

Замечание. Напомним: соотношение (25.6) означает, что для любого е > О

Отсюда следует, что для состоятельной оценки 0 (,,) (Х (,,) ) ее отклонение от 0 не менее чем на сколь угодно малую величину е становится при большом объеме выборки п событием, близким к невозможному. Иными словами, состоятельность оценки — это возможность определить с ее помощью искомый параметр с любой точностью и сколь угодно большой достоверностью за счет использования выборки достаточно большого объема п.

Пример 25.5. Выборочное среднее х = — У х,- — состоятельная

оценка математического ожидания т_х генеральной совокупности X с конечной дисперсией 2 _х.

Замечание. Состоятельность оценки х в конечном счете обеспе- о 2

вать следующее обобщение результата примера 25.5: если статистика 0(«)(Х Л )) является асимптотически несмещенной оценкой параметра 0 и lim Z)[0 (,,) (X (W) )] = 0, то эта статистика есть состоятельная оценка

Пример 25.6. Докажем, что выборочные дисперсии Sq =

= — Y (х,— х) 2 и S 2 =—‘V(x_j-x) 2 являются состоятельными

оценками дисперсии o;_v генеральной совокупности X, имеющей ко- нечный центральный момент р₄[Лф

? Воспользуемся равенством (25.4):

Из состоятельности выборочного среднего как оценки параметра т_х(см. пример 25.5) следует, что

Из (25.4), (25.7) и (25.8) следует, что Sq— ^ >о_х при п —> ©о, т.е.

S₀ — состоятельная оценка дисперсии а_х. Далее S =-^, причем

Замечание. Можно доказать, что все выборочные начальные и центральные моменты (24.3), (24.5) являются состоятельными оценками соответствующих моментов генеральной совокупности, если последние существуют.

3. Эффективность точечной оценки

Пусть имеются две несмещенные оценки 0| л) (х (л) ) и 0 ( ₂ и) (х (я) ) одного и того же параметра 0. Если для любого не N выполняется неравенство

то следует предпочесть оценку б< я) (х (я) ), так как ее разброс относительно искомого значения 0 в среднем меньше и, следовательно, она при одном и том же п дает в среднем более точный результат. В таких случаях говорят, что оценка 0|» ) (х (/,) ) эффективнее оценки 0 ( ₂ w) (x (w) ).

Определение. Если существует такая несмещенная оценка 0i’°(x (/,) ) параметра 0, что для любой другой его несмещенной оценки 0 (,,) (х (я) ) при всех п е N выполняется неравенство

то 0 ( *’ г) (х (я) ) называют эффективной оценкой параметра 0.

1. В отличие от несмещенности и состоятельности эффективность оценки 0 ( ‘°(х (,,) ) зависит от закона распределения генеральной совокупности X: для одного закона 0 (,,) (х (,г) ) может оказаться эффективной, а для другого — нет.

2. При выполнении определенных требований кЛТи 0 ” ) (х (,,) ) (они выполняются для основных законов распределения и большинства оценок, используемых в приложениях), справедливо неравенство Крамера—Рао:

Это неравенство можно использовать для проверки эффективности оценок следующим образом. Пусть для некоторой несмещенной оценки 0 (л) (х (л) ) неравенство (25.9) превращается в равенство. Это означает, что дисперсия Z>[0 (w) (X (/,) )] достигла нижней границы для дисперсий всех несмещенных оценок параметра 0, т.е. оценка 0 ( /О(_х ( «))

Пример 25.7. Пусть X

N(m, о). Исследуем эффективность не- 1 V

? Левая часть неравенства (25.9) уже найдена, см. (25.3): Подсчитаем выражение в правой части (25.9). В данном случае

Отсюда находим правую часть неравенства (25.9):-= —.

х = — ^Xj — это эффективная оценка математического ожидания т 1=1

Пример 25.8. Покажем, что выборочное среднее х = — яв-

ляется эффективной оценкой параметра X распределения Пуассона.

Левая часть неравенства (25.9) равна D[X] = = —.

Найдем правую часть:

Итак, правая часть в (25.9) равна —, т.е. совпадает с левой частью.

Поэтому выборочное среднее х = — является эффективной оценкой

параметра X для генеральной совокупности X

Пример 25.9. Пусть генеральная совокупность — это число появлений события А (успеха), вероятность которого Р(А) = р е (0; 1), в п испытаниях, т.е. X

Исследовать относительную частоту успеха р(х) = — как оценку

т.е. р есть несмещенная оценка параметра р.

б) Состоятельность. Из теоремы 23.4 (закон больших чисел в формулировке Бернулли) непосредственно следует, что

а это означает состоятельность оценки р параметра р.

в) Эффективность. С учетом того что D[X] = npq (см. п. 22.10), вычислим левую часть неравенства (25.9):

Найдем теперь правую часть (25.9). Для X

В(п, р) имеем (см. п. 22.10):

т.е. правая часть в (25.9) равна — и совпадает с левой частью. Это

означает, что р есть эффективная оценка параметра р.

Источник

Математическая статистика

Точечные оценки

Методы получения точечных оценок

Точечной оценкой неизвестного параметра θ, вообще говоря, может являться любая статистика. Однако на практике интерес представляют лишь наиболее «качественные» оценки, для которых вероятность того, что при реализации случайной выборки они примут значение максимально близкое к неизвестному значению θ наибольшая. Такие оценки должны быть несмещёнными, состоятельными и эффективными. Возникает вопрос, как получить качественную оценку для произвольного параметра θ наблюдаемой случайной величины X?

1. Метод подстановки

Например, согласно методу подстановки оценкой математического ожидания будет выборочное среднее, а оценкой дисперсии – выборочная дисперсия.

Все оценки, рассчитанные по методу подстановки, являются состоятельными, однако их несмещённость и эффективность не гарантированы. Примером смещённой оценки, рассмотренной ранее, является выборочная дисперсия.

Метод моментов состоит нахождении такого вектора параметров θ, при котором теоретические моменты равны выборочным моментам, т.е. в разрешении системы уравнений вида:

Число уравнений в системе (1) равно числу неизвестных параметров k. Для получения оценок по методу моментов, вообще говоря, могут быть выбраны любые моменты произвольных порядков, однако, как правило, на практике используют лишь моменты низших порядков.

Все оценки, рассчитанные по методу моментов, являются состоятельными, однако их несмещённость и эффективность, так же, как и в случае метода подстановки, не гарантированы.

Точечные оценки, полученные по методу моментов, называются ММ-оценками.

Пример 1

3. Метод максимального правдоподобия

Метод максимального правдоподобия (maximum likelihood estimation, MLE) является наиболее популярным методом оценивания неизвестных параметров распределений.

Учитывая, что компоненты X₁,…, X_n случайной выборки, реализациями которых являются выборочные значения x ₁,…,x_n, независимы, многомерная функция плотности есть произведение одномерных функций плотностей:

В (2) учтено, что все компоненты X₁,…, X_n имеют одинаковое распределение, совпадающее с распределением генеральной совокупности X.

Функция правдоподобия выборки x₁,…, x_n является функцией только вектора неизвестных параметров θ.

Запишем необходимое условие экстремума функции правдоподобия:

На практике бывает удобно вместо системы уравнений (3) составить систему уравнений

Все оценки, рассчитанные по методу максимального правдоподобия, являются состоятельными и, по крайней мере, асимптотически несмещёнными и асимптотически эффективными. Если для неизвестного параметра существует эффективная оценка, то метод максимального правдоподобия даёт именно эту оценку.

Точечные оценки, полученные по методу максимального правдоподобия, называются МП-оценками.

Источник