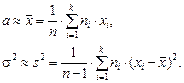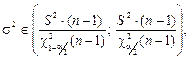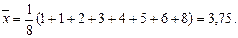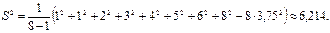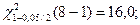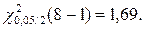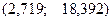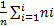точечная оценка параметра распределения равна 20 тогда его интервальная оценка может иметь вид

Тесты по курсу: «Теория вероятностей и математическая статистика» (стр. 3 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3

Вопрос 104. Закон распределения системы двух дискретных случайных величин Х и Y задан таблицей распределения:

Вопрос 105. Закон распределения системы двух дискретных случайных величин Х и Y задан таблицей распределения:

Вопрос 106. Закон распределения системы двух дискретных случайных величин Х и Y задан таблицей распределения:

Тема 4. Функции случайных величин

Вопрос 107. Дискретная случайная величина Х задана законом распределения вероятностей:

Тогда математическое ожидание случайной величины Y = 3X равно…

Вопрос 108. Дискретная случайная величина Х задана законом распределения вероятностей:

Тогда математическое ожидание случайной величины Y = 4X равно…

Вопрос 109. Дискретная случайная величина Х задана законом распределения вероятностей:

Тогда математическое ожидание случайной величины Y = 5X равно…

Вопрос 110. Дискретная случайная величина Х задана законом распределения вероятностей:

Тогда математическое ожидание случайной величины Y = 6X равно…

Вопрос 111. Дискретная случайная величина Х задана законом распределения вероятностей:

Тогда математическое ожидание случайной величины Y = 2X равно…

Раздел 2. Математическая статистика

Тема 1. Основные понятия. Точечные оценки.

Вопрос 112. Мода вариационного ряда 1, 2, 3, 3, 4, 7 равна…

Вопрос 113. Мода вариационного ряда 1, 2, 3, 4, 4, 6 равна…

Вопрос 114. Мода вариационного ряда 1, 1, 2, 5, 7, 8 равна…

Вопрос 115. Мода вариационного ряда 1, 3, 5, 5, 6, 7 равна…

Вопрос 116. Мода вариационного ряда 1,2,4,4,5,6 равна…

Вопрос 117. Из генеральной совокупности извлечена выборка объема n=60, полигон частот которой имеет вид

Тогда число вариант xi = 2 в выборке равно…

Вопрос 118. Из генеральной совокупности извлечена выборка объема n=40, полигон частот которой имеет вид

Тогда число вариант xi = 4 в выборке равно…

Вопрос 119. Из генеральной совокупности извлечена выборка объема n = 70, полигон частот которой имеет вид

Тогда число вариант xi = 1 в выборке равно…

Вопрос 120. Из генеральной совокупности извлечена выборка объема n = 80, полигон частот которой имеет вид

Тогда число вариант xi = 3 в выборке равно…

Тогда число вариант xi = 3 в выборке равно…

Вопрос 122. Из генеральной совокупности извлечена выборка объема n = 50:

Вопрос 123. Из генеральной совокупности извлечена выборка объема n = 50:

Вопрос 124. Из генеральной совокупности извлечена выборка объема n = 50:

Вопрос 125. Из генеральной совокупности извлечена выборка объема n = 50:

Вопрос 126. Из генеральной совокупности извлечена выборка объема n = 50:

Вопрос 127. По выборке объема n=100 построена гистограмма частот:

Тогда значение а равно…

Вопрос 128. По выборке объема n = 100 построена гистограмма частот:

Тогда значение а равно…

Вопрос 129. По выборке объема n = 100 построена гистограмма частот:

Тогда значение а равно…

Вопрос 130. По выборке объема n = 100 построена гистограмма частот:

Тогда значение а равно…

Вопрос 131. По выборке объема n=100 построена гистограмма частот:

Тогда значение а равно…

Вопрос 132. Проведено 5 измерений (без систематических ошибок) некоторой случайной величины: 5, 6, 9, 10, 11. Тогда несмещенная оценка математического ожидания равна…

Вопрос 133. Проведено 5 измерений (без систематических ошибок) некоторой случайной величины: 6, 7, 8, 10, 11. Тогда несмещенная оценка математического ожидания равна…

Вопрос 134. Проведено 5 измерений (без систематических ошибок) некоторой случайной величины: 7, 8, 9, 11, 12. Тогда несмещенная оценка математического ожидания равна…

Вопрос 135. Проведено 5 измерений (без систематических ошибок) некоторой случайной величины: 8, 9, 10, 12, 13. Тогда несмещенная оценка математического ожидания равна…

Вопрос 136. Проведено 5 измерений (без систематических ошибок) некоторой случайной величины: 9, 10, 11, 13, 14. Тогда несмещенная оценка математического ожидания равна…

Вопрос 137. В результате измерений некоторой физической величины одним прибором (без систематических ошибок) получены следующие результаты (в мм): 10, 13, 13. Тогда несмещенная оценка дисперсии измерений равна…

Вопрос 138. В результате измерений некоторой физической величины одним прибором (без систематических ошибок) получены следующие результаты (в мм): 13, 14, 15. Тогда несмещенная оценка дисперсии измерений равна…

Вопрос 139. В результате измерений некоторой физической величины одним прибором (без систематических ошибок) получены следующие результаты (в мм): 14, 17, 17. Тогда несмещенная оценка дисперсии измерений равна…

Вопрос 140. В результате измерений некоторой физической величины одним прибором (без систематических ошибок) получены следующие результаты (в мм): 8, 10, 12. Тогда несмещенная оценка дисперсии измерений равна…

Вопрос 141. В результате измерений некоторой физической величины одним прибором (без систематических ошибок) получены следующие результаты (в мм): 8, 11, 11. Тогда несмещенная оценка дисперсии измерений равна…

Тема 2. Интервальные оценки

Вопрос 142. Точечная оценка параметра распределения равна 21. Тогда его интервальная оценка может иметь вид…

Вопрос 143. Точечная оценка параметра распределения равна 22. Тогда его интервальная оценка может иметь вид…

Вопрос 144. Точечная оценка параметра распределения равна 23. Тогда его интервальная оценка может иметь вид…

Вопрос 145. Точечная оценка параметра распределения равна 24. Тогда его интервальная оценка может иметь вид…

Тема 3. Статистическая проверка гипотез

Вопрос 146. Если основная гипотеза имеет вид H 0 : a =15, то конкурирующей может быть гипотеза …

Вопрос 147. Если основная гипотеза имеет вид H 0 : a =16, то конкурирующей может быть гипотеза …

Вопрос 148. Если основная гипотеза имеет вид H 0 : a =17, то конкурирующей может быть гипотеза …

Вопрос 149. Если основная гипотеза имеет вид H 0 : a =18, то конкурирующей может быть гипотеза …

Вопрос 150. Если основная гипотеза имеет вид H 0 : a =19, то конкурирующей может быть гипотеза …

Источник

Ответы на все модули (для контрольного теста) по предмету «Математическая статистика»

Ответы на все модули (для контрольного теста) по предмету «Математическая статистика»

По выборке объема n=100 построена гистограмма частот:

Тогда значение а равно…

Формула Стерджесса для определения оптимального числа групп k при группировке данных статистической совокупности имеет вид (N – число единиц в совокупности):

Определение искомой характеристики генеральной совокупности внутри какого-то интервала с заданной вероятностью, называется

Интервальной оценкой

Вариант дискретного вариационного ряда, имеющий наибольшую частоту, называется

Модой

Наиболее часто встречающееся значение признака у единиц данной статистической совокупности – это:

Мода

К основным задачам математической статистики относится:

расчет числовых характеристик теоретических распределений вероятностей

В результате измерений некоторой физической величины одним прибором (без систематических ошибок) получены следующие результаты: 10, 13, 13. Тогда несмещенная оценка дисперсии измерений равна

Если количественный признак изменяется непрерывно или принимает много значений, то соответствующий вариационный ряд называется

Интервальным

Если количественный признак принимает дискретные значения, то соответствующий вариационный ряд называется

Дискретным

Из генеральной совокупности извлечена выборка объемом n = 49, полигон частот которой имеет вид:

тогда число выборочных значений (число вариант) для x_i = 3 равно …

По городской телефонной сети было произведено 100 наблюдений и установлено, что средняя продолжительность телефонного разговора составляет 4 минут при среднеквадратичном отклонении 2 мин. Предельная ошибка выборки с вероятностью 0,954 составляет

В результате 10 опытов получены следующие выборочные значения: 3; 3; 4; 4; 4; 5; 5; 5; 6; 6. Законом распределения для выборки является

Источник

Тема 15. Математическая статистика. Интервальные оценки параметров распределения. Непрерывное и дискретное распределения признаков

1. Проведено четыре измерения (без систематических ошибок) некоторой случайной величины (в мм): 4, 7, 8, 9. Тогда несмещённая оценка математического ожидания равна…

2. Проведено четыре измерения (без систематических ошибок) некоторой случайной величины (в мм): 3, 8, 9, 16. Тогда несмещённая оценка математического ожидания равна…

3. Проведено четыре измерения (без систематических ошибок) некоторой случайной величины (в мм): 4, 5, 6, 9. Тогда несмещённая оценка математического ожидания равна…

4. Проведено четыре измерения (без систематических ошибок) некоторой случайной величины (в мм): 2, 3, 7, 9. Тогда несмещённая оценка математического ожидания равна…

5. Проведено четыре измерения (без систематических ошибок) некоторой случайной величины (в мм): 2, 3, 6, 9. Тогда несмещённая оценка математического ожидания равна…

6. Точечная оценка математического ожидания нормального распределения равна 12. Тогда его интервальная оценка может иметь вид …

7. Точечная оценка математического ожидания нормального распределения равна 13. Тогда его интервальная оценка может иметь вид …

8. Точечная оценка математического ожидания нормального распределения равна 13. Тогда его интервальная оценка может иметь вид.

9. Точечная оценка математического ожидания нормального распределения равна 15. Тогда его интервальная оценка может иметь вид.

10. Точечная оценка математического ожидания нормального распределения равна 16. Тогда его интервальная оценка может иметь вид.

11. Точечная оценка математического ожидания нормального распределения равна 10. Тогда его интервальная оценка может иметь вид …

12. Точечная оценка математического ожидания нормального распределения равна 11. Тогда его интервальная оценка может иметь вид …

13. Точечная оценка математического ожидания нормального распределения равна 13. Тогда его интервальная оценка может иметь вид…

14. Точечная оценка математического ожидания нормального распределения равна 11. Тогда его интервальная оценка может иметь вид.

15. Точечная оценка математического ожидания нормального распределения равна 13. Тогда его интервальная оценка может иметь вид.

16. Точечная оценка математического ожидания нормального распределения равна 14. Тогда его интервальная оценка может иметь вид.

17. Точечная оценка математического ожидания нормального распределения равна 17. Тогда его интервальная оценка может иметь вид.

18. Точечная оценка математического ожидания нормального распределения равна 18. Тогда его интервальная оценка может иметь вид.

19. Точечная оценка математического ожидания нормального распределения равна 10. Тогда его интервальная оценка может иметь вид.

20. Точечная оценка математического ожидания нормального распределения равна 15. Тогда его интервальная оценка может иметь вид.

21. Точечная оценка математического ожидания нормального распределения равна 12. Тогда его интервальная оценка может иметь вид.

22. Точечная оценка математического ожидания нормального распределения равна 16. Тогда его интервальная оценка может иметь вид.

23. Точечная оценка математического ожидания нормального распределения равна 17. Тогда его интервальная оценка может иметь вид.

24. Точечная оценка математического ожидания нормального распределения равна 18. Тогда его интервальная оценка может иметь вид.

25. Точечная оценка математического ожидания нормального распределения равна 14. Тогда его интервальная оценка может иметь вид.

26. Точечная оценка математического ожидания нормального распределения равна 12. Тогда его интервальная оценка может иметь вид.

27. Точечная оценка математического ожидания нормального распределения равна 10. Тогда его интервальная оценка может иметь вид.

28. Точечная оценка математического ожидания нормального распределения равна 11. Тогда его интервальная оценка может иметь вид.

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.

Источник

Точечная оценка параметров распределения

Тема 7. Статистические оценки параметров распределения: точечные и интервальные оценки

Смысл статистических методов заключается в том, чтобы по выборке ограниченного объема, то есть по некоторой части генеральной совокупности, высказать обоснованное суждение о ее свойствах целиком.

Естественно, что замена исследования генеральной совокупно­сти исследованием выборки порождает ряд вопросов:

1. В какой степени выборка отражает свойства генеральной совокупности, т. е. в какой степени выборка репрезентативна по отношению к генеральной совокупности?

2. Какую информацию о значениях параметров генеральной совокупности могут дать параметры выборки?

3. Можно ли утверждать, что полученные выборочным путем статистические характеристики (средние величины, дисперсия или любые другие производные величины) равны тем характе­ристикам, которые могут быть получены из генеральной сово­купности.

Проверка показывает, что значения параметров, полученных для разных выборок из одной генеральной совокупности, обыч­но не совпадают. Рассчитанные выборочным путем числовые значения параметров выборок являются лишь результатом при­ближенного статистического оценивания значений этих парамет­ров в генеральной совокупности. Статистическое оценивание, в силу изменчивости наблюдаемых явлений, позволяет получать только их приближенные значения.

Примечание. Строго говоря, в статистике оценка — это правило вычисления оцениваемого параметра, а термин оценить, т. е. провести оценивание, означает указать приближенное значе­ние.

Различают оценки точечные и оценки интервальные.

Точечная оценка параметров распределения

Пусть x₁, x₂, …, x_n – выборка объема n из генеральной совокупности с функцией распределения F(x).

Числовые характеристики этой выборки называются выборочными (эмпирическими) числовыми характеристиками.

Отметим, что выборочные числовые характеристики являются характеристиками данной выборки, но не являются характеристиками распределения генеральной совокупности. Однако эти характеристики можно использовать для оценок параметров генеральной совокупности.

Точечной называют статистическую оценку, которая определяется одним числом.

Точечная оценка характеризуется свойствами:несмещенность, состоятельность и эффективность.

Несмещенной называют точечную оценку, математическое ожидание которой равно оцениваемому параметру при любом объеме выборки.

Точечная оценка называется состоятельной, если при неограниченном увеличении объема выборки (n ® ¥) она сходится по вероятности к истинному значению параметра, то есть стремится к истинному значению оцениваемого параметра генеральной совокупности.

Эффективной называют точечную оценку, которая (при заданном объеме выборки n) имеет наименьшую возможную дисперсию, те есть гарантирует наименьшее отклонение выборочной оценки от такой же оценки генеральной совокупности..

В математической статистике показывается, что состоятельной, несмещенной оценкой генерального среднего значения а является выборочное средне:

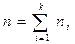
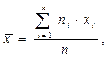
где х_i – варианта выборки, n_i – частота варианты х_i, – объем выборки.

Несмещенной оценкой генеральной дисперсии служит исправления выборочная дисперсия

,

Более удобна формула .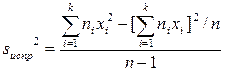

Оценка s 2 для генеральной дисперсии является также и состоятельной, но не является эффективной. Однако в случае нормального распределения она является «асимптотически эффективной», то есть при увеличении n отношение ее дисперсии к минимально возможной неограниченно приближается к единице.

Точечные оценки имеют тот недостаток, что при малом объеме выборки могут значительно отличаться от оцениваемых параметров. Поэтому, чтобы получить представление о близости между параметром и его оценкой, в математической статистике вводятся, так называемые, интервальные оценки.

Доверительный интервал

Если при статистической обработке результатов требуется найти не только точечную оценку неизвестного параметра θ, но и охарактеризовать точность этой оценки, то находится доверительный интервал.

Доверительный интервал – это интервал, в котором заранее заданной доверительной вероятностью находится неизвестный параметр генеральной совокупности.

Доверительная вероятность – это вероятность, с которой неизвестный параметр генеральной совокупности принадлежит доверительному интервалу.

Обычно принимают р = 0,95 или (реже) 0,99. Эти вероятности признаны достаточными для уверенного суждения о генеральных параметрах на основании известных выборочных показателей.

Доверительный интервал для математического ожидания имеет вид: где S – СКО, — критическое значение распределения Стьюдента (Смотри ПРИЛОЖЕНИЕ 1 к Теме 7)

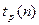
Доверительный интервал для дисперсии имеет вид

где 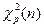— обратное распределение хи-квадрат (Смотри ПРИЛОЖЕНИЕ 2 к Теме 7)

ЗАДАЧА. Дана выборка 5, 6, 8, 2, 3, 1, 1, 4. Записать данные в виде вариационного ряда. Определить оценки среднего, дисперсии, и стандартного отклонения а также построить доверительные интервалы для среднего и дисперсии на уровне значимости a=0,05.

Решение. Представим данные в виде вариационного ряда: 1, 1, 2, 3, 4, 5, 6, 8. Так как n = 8, то выборочное среднее и исправленная выборочная дисперсия равны

Стандартное отклонение .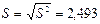

По таблицам из ПРИЛОЖЕНИЯ 1 и ПРИЛОЖЕНИЯ 2 к Теме 7. находим: ,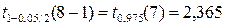

Получаем доверительный интервал для математического ожидания

или .

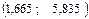
Доверительный интервал для дисперсии

или

Источник

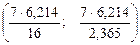
выборочной совокупностью

Медиана

Завод отправил на базу 500 доброкачественных изделий. Вероятность того, что в пути изделие повредится, равна 0,002. Найти вероятность того, что на базу придут 3 негодных изделия. 0,06

Если основная гипотеза имеет вид Н₀:а=10, то конкурирующей гипотезой является… Н₁:а>10

Если среди прочих несмещенных оценок того же параметра несмещенная оценка Ѳ_n * параметра Ѳ обладает наименьшей дисперсией называется эффективной

Если основная гипотеза имеет вид Н₀:а=20, то конкурирующей гипотезой может быть гипотеза… (Н₁ :а≥20; Н₁ :а=10; Н₁ :а≥10; Н₁ :а≤20)

Если при любом объеме выборки n математическое ожидание равно оцениваемому параметру Ѳ, то есть М (Ѳ_n * )= Ѳ, то такая оценка называется: несмещенной

Из 30 участников собрания надо выбрать председателя и секретаря. Сколькими способами это можно сделать? 870

Интервал (Ѳ_n *(1) ;Ѳ_n *(2) ) относительно которого можно утверждать с определенной, близкой к единице вероятностью γ, что он содержит неизвестное значение Ѳ называется: Интервальная оценка параметра Ѳ

Из генеральной совокупности извлечена выборка объема n=50

Из 25 экзаменационных билетов по геометрии ученик успел подготовить 11 первых и 8 последних билетов. Какова вероятность того, что на экзамене ему достанется билет, который он не подготовил? 0,24

Какова вероятность того, что при бросании игрального кубика выпадет 5 очков?1/5

Какова вероятность того, что при бросании игрального кубика выпадет более 3 очков?1/3

Математическое ожидание алгебраичной суммы случайной и постоянной величины равно; алгебраической сумме этой константы мат.ожидания случайной величины-ответ

На химическом заводе установлена система аварийной сигнализации. Когда возникает аварийная ситуация, звуковой сигнал срабатывает с вероятностью 0,95. Звуковой сигнал может сработать случайно и без аварийной ситуации с вероятностью 0,02. Реальная вероятность аварийной ситуации равна 0,004. Предположим, что звуковой сигнал сработал. Какова вероятность того, что сигнал сработал случайно, без аварийной ситуации? ( 0,95; 2; 0,004; 1,1602)

На соревнования по легкой атлетике приехала команда из 12 спортсменок. Сколькими способами тренер может определить, кто из них побежит в эстафете 4х100 м на первом, втором, третьем и четвертом этапах? (5940; 495; 11880; 1)

На химическом заводе установлена система аварийной сигнализации. Когда возникает аварийная ситуация, звуковой сигнал срабатывает с вероятностью 0,95. Звуковой сигнал может сработать случайно и без аварийной ситуации с вероятностью 0,02. Реальная вероятность аварийной ситуации равна 0,004. Предположим, что звуковой сигнал сработал. Чему равна вероятность реальной аварийной ситуации? (1; 0,6; 0,4118; 0,5882)

Наиболее часто встречающееся значение признака называется: модой

На кануне важного референдума было решено провести выборочный опрос. Примерное распределение голосов было известно – около 20% воздержавшихся, остальные поровну «за» и «против». Сколько надо опросить людей, чтобы с вероятностью 0,9 гарантировать отклонение числа опрошенных «за» от истинного не более чем на 2% от всего электората:

(8900; 10000; 9870; 6700)

На станции 7 запасных путей. Сколькими способами можно расставить на них 4 поезда? (Поезда отличаются друг от друга) 840

Относительно игрального кубика появилось подозрение, что грань с шестеркой тяжелее других, в силу чего вероятность выпадения шестерки не намного, но больше 1/6. Какое число бросков кубика гарантирует с вероятностью 0,9, что отклонение частоты от вероятности выпадения шестерки не превышает 0,04: ( n≤268; n≤69; n

Одна из центральных теорем в теории вероятностей, устанавливающая точную связь между частотой вероятностью события: теорема Бернулли

Однозначно определенное правило, устанавливающее условия, при которых проверяемую гипотезу по результатам наблюдений следует либо отвергнуть, либо не отвергнуть понимают: статистический критерий

Пусть всхожесть семян данного растения составляет 90%. Найти вероятность того, что из четырех посеянных семян взойдут три: 0,9

Пусть всхожесть семян данного растения составляет 90%. Найти вероятность того, что из четырех посеянных семян взойдут не менее трех: 0,9477

Предприниматель хочет отправить рекламные объявления в три из семи городских газет. Сколькими способами можно выбрать эти 3 газеты? 35

При использовании статистического критерия возможен следующий случай: (гипотеза верна и ее принимают согласно критерию; гипотеза неверна, но ее отвергают согласно критерию; гипотеза не выдвигаема; гипотеза верна и ее отвергают согласно критерию)

При игре в карты пользуются колодой из 36 карт. Какова вероятность того, что первой сданной картой будет карта мастик «пик»? ¼

При условии равно вероятности рождения мальчика и девочки вероятность того, что из 1000 родившихся детей мальчиков будет от 465 до 535, не меньше числа …

При большой выборке оценка Ѳ_n * параметра Ѳ называется: состоятельной

При изготовлении отливок получается 20% дефективных. Сколько необходимо запланировать отливок к изготовлению, чтобы с вероятностью 0,95 получилось не менее 50 бездефектных: (n>68; n≥6; n≥9; n≥69)

Сколькими способами можно изготовить трехцветный флаг с горизонтальными полосами, если имеется материал 7 различных цветов? 210

Статистическое распределение выборки имеет вид

Тогда относительная частота варианты х_1=2, равна … ( 0,1; 0,2; 4; 1)

Статистический критерий не дает: (Логического доказательства; статистического критерия; статистическую гипотезу; конкурирующую гипотезу)

Сколькими способами можно отобрать стартовую шестерку в волейбольном матче, если в команде заявлено 10 игроков? 210

Средняя арифметическая определяется по формуле: Х_ср.=

Сколькими способами могут занять первое, второе и третье места 8 участниц финального забега на дистанции 100м? ( у меня получилось 336, такого ответа в тесте нет!)Отеты:24; 800;2;56

Случайная величина Х имеет нормальный закон распределения с параметрами а и σ. Если известно, что σ =1,2 и Р(Х >3)=0,5, то значение параметра а равно… (3; 1;0,3; 4,5)

Случайная величина Х подчинена закону распределения с плотностью вероятности φ(х). Тогда вероятность попадания случайной величины Х в интервале (15;45) не меньше числа…..(80; 30; 18; 42)

Случайная величина распределена равномерно на интервале (10;12). Тогда ее математическое ожидание и дисперсия соответственно равны… (10,5 и 1/3; 11и 1; 10 и 2; 11 и 1/3)

Совокупность n объектов, отобранных из исследуемой генеральной совокупности называется:

выборочной совокупностью

Совместное действие большого числа случайных факторов приводит к результату, почти не зависящему от случая отражает смысл: закон больших чисел

Случайная величина Х задана интегральной функцией распределения

Найти вероятность того, что в результате испытания Х примет значение, полуинтервалу [0;2)

Сколькими способами можно выбрать 49 предметов из 50предметов 2450-ответ

Точечная оценка математического ожидания нормального распределения равна 10.Тогда его интервальная оценка может иметь вид… (8,5; 11,5)

Функция плотности нормального закона распределения имеет вид:

Функция которая в результате опыта может принять тот или иной вид,неизвестно заранее –какой именно называется называется Случайной функцей-ответ

Число членов, образующих генеральную совокупность называется: объемом генеральной совокупности

Источник