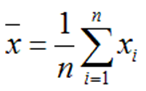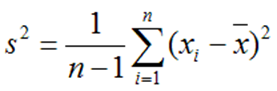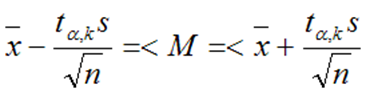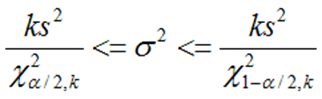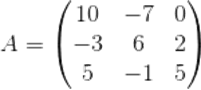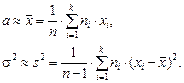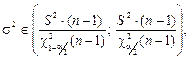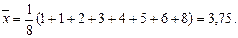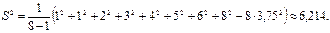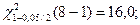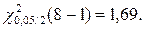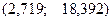точечное и интервальное оценивание параметров распределения

ТОЧЕЧНЫЕ И ИНТЕРВАЛЬНЫЕ ОЦЕНКИ

Вычисление интервальной оценки рассмотрим на примере интервальной оценки МО для случайной величины подчиняющейся нормальному закону распределения. Границы доверительного интервала определятся по формулам:

X_max = X + T(ν,P)*S/(n) 1/2

Погрешности средств измерений и измерительных каналов средств автоматизации могут быть выражены двумя различными способами: с помощью точечных оценок и с помощью интервальных. К точечным оценкамотносится математическое ожидание погрешности и среднеквадратическое отклонение.В качестве интервальной оценкииспользуют интервал погрешности, который охватывает все возможные значения погрешности измерений с вероятностью .Эта вероятность называется доверительной или надежностью оценки погрешности.

Предел допускаемой погрешности можно рассматривать как точечную оценку или как интервальную для доверительной вероятности, равной единице.

Интервальная оценка является более гибкой, поскольку она позволяет указать погрешность измерений в зависимости от того, какая требуется вероятность реализации этой погрешности для конкретных условий эксплуатации средства измерений.

Смысл интервальной оценки погрешности иллюстрируется рис. 4.3. Здесь использованы следующие обозначения: — погрешность измерения; — плотность распределения погрешностей ; — функция распределения погрешностей, .Для нормального закона распределения погрешностей (закона Гаусса) плотность распределения центрированной случайной величины описывается функцией , где — среднеквадратическая погрешность.

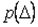
Если погрешность измерения находится внутри интервала , то вероятность этого события вычисляется как

.

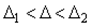
(4.35)

В наиболее типичном случае симметричных границ ( ) получим

.

(4.36)

Здесь использовано свойство симметрии функции распределения для закона Гаусса.

Таким образом, если задан интервал , который содержит в себе погрешность измеряемого параметра , то вероятность того, что погрешность не выходит за границы интервала, можно найти по формуле (4.36) для нормального закона распределения. Вероятность называют также надежностью оценки погрешности и обозначают символом :

.

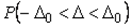
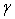
(4.37)

Для вычисления функции распределения удобно использовать пакеты MathCAD, Matlab.С их помощью из формулы (4.37) несложно найти величину доверительного интервала , если задана величина надежности .

Для доверительная вероятность =68,3%; для =95,3%; для =99,7% и для = 99,994%.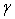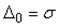

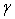
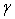
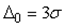
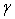
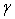
Для увеличения надежности оценки погрешности измерений или для сужения доверительного интервала при заданной надежности можно использовать усреднение результатов многократных измерений. Поскольку оценка среднеквадратической погрешности результата усреднения равна (см. (3.2)), где — среднеквадратическая погрешность средства измерений, — количество однократных измерений, то, подставив в (4.37) вместо величину , получим

.

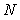
(4.38)

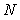
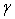
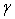
Эта формула позволяет найти количество однократных измерений , которое необходимо усреднить для получения требуемого доверительного интервала при заданной надежности или требуемой надежности при заданном доверительном интервале .Поскольку формула (4.38) задана в неявном виде, для нахождения требуемых неизвестных следует воспользоваться математическими пакетами для компьютерных вычислений.

Следует иметь в виду, что повышение точности путем усреднения результатов многократных измерений имеет множество ограничений.

Проблемой использования интервального метода оценки погрешности является необходимость знания закона распределения погрешностей.

Отметим, что доверительные интервалы, полученные из рассеяния множества измерений, никак не учитывают систематическую погрешность измерений.Систематическую погрешность или наличие ошибки в постановке эксперимента, в учете факторов, о существовании которых мы не знаем, оценить невозможно, не имея более точного измерительного прибора.

Непрерывная случайная величина может принимать любое значение в некотором конечном или бесконечном интервале (например, разрывная длина бумаги).При испытаниях часто получают выборку значений непрерывной случайной величины с некоторым распределением вероятности получения того или иного значения.Наиболее часто встречается нормальное распределение.Точнее, реальные распределения в большинстве случаев достаточно близки к нормальному.

Основные параметры нормального распределения – математическое ожидание М случайной величины и её генеральное среднеквадратическое отклонение (СКО) σ (или генеральная дисперсия σ 2 ).Математическое ожидание – это центр группировки результатов испытаний, при отсутствии систематических погрешностей соответствует количественной характеристике объекта испытаний.Дисперсия (или СКО) – мера рассеяния результатов испытаний.Найти их значения абсолютно точно невозможно. Однако при объёме выборки n не менее 25…30 обычно считают, что точечные оценки параметров нормального распределения с приемлемой точностью равны параметрам. Кроме того, можно достаточно точно рассчитать генеральную дисперсию при проведении серий испытаний, в которых генеральная дисперсия не меняется (вычисление дисперсии по текущим измерениям), например, при приёмо-сдаточных испытаниях.

Применяется также мера рассеяния, называемая коэффициентом вариации. Генеральный коэффициент вариации

Выборочный коэффициент вариации

(1.2)

Точечной оценкой математического ожидания М является среднее значение выборки :

Точечной оценкой генеральной дисперсии является выборочная несмещенная дисперсия:

По текущим измерениям дисперсия может быть вычислена по формуле

Здесь n_i – объем испытаний (объём выборки) в каждой серии, s_i 2 – дисперсии в соответствующих сериях, m – количество серий.

Точечные оценки малоинформативны, поскольку являются случайными величинами и могут значительно отличаться от оцениваемо-го параметра.Для повышения информативности используют интер-вальные оценки (рассчитывают доверительные интервалы).

При достаточно точно известной генеральной дисперсии σ 2 ) доверительный интервал для математического ожидания определяют из соотношения

(1.3)

Если генеральная дисперсия неизвестна, доверительный интервал для математического ожидания определяют из соотношения

Здесь t_α;k – коэффициент Стьюдента, k=n-1 – число степеней свободы. Доверительный интервал для дисперсии определяют из соотношения:

Извлекая из всех частей неравенства квадратный корень, можно получить интервальную оценку СКО.

LU-метод

LU-разложение — это представление матрицы A в виде A=L•U, где L — нижнетреугольная матрица с еденичной диагональю, а U — верхнетреугольная матрица. LU-разложение является модификациеё метода Гаусса.Основные применения данного алгоритма — решение систем алгебраических уравнений, вычисление определителя, вычисление обратной матрицы и др.

Рассмотрим алгоритм на примере матрицы

Алгоритм

и

2. Для каждого столбца j = 1… 3 матрицы будем вычислять как

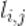
Для каждой строки вычислим

Источник

Точечная оценка параметров распределения

Тема 7. Статистические оценки параметров распределения: точечные и интервальные оценки

Смысл статистических методов заключается в том, чтобы по выборке ограниченного объема, то есть по некоторой части генеральной совокупности, высказать обоснованное суждение о ее свойствах целиком.

Естественно, что замена исследования генеральной совокупно­сти исследованием выборки порождает ряд вопросов:

1. В какой степени выборка отражает свойства генеральной совокупности, т. е. в какой степени выборка репрезентативна по отношению к генеральной совокупности?

2. Какую информацию о значениях параметров генеральной совокупности могут дать параметры выборки?

3. Можно ли утверждать, что полученные выборочным путем статистические характеристики (средние величины, дисперсия или любые другие производные величины) равны тем характе­ристикам, которые могут быть получены из генеральной сово­купности.

Проверка показывает, что значения параметров, полученных для разных выборок из одной генеральной совокупности, обыч­но не совпадают. Рассчитанные выборочным путем числовые значения параметров выборок являются лишь результатом при­ближенного статистического оценивания значений этих парамет­ров в генеральной совокупности. Статистическое оценивание, в силу изменчивости наблюдаемых явлений, позволяет получать только их приближенные значения.

Примечание. Строго говоря, в статистике оценка — это правило вычисления оцениваемого параметра, а термин оценить, т. е. провести оценивание, означает указать приближенное значе­ние.

Различают оценки точечные и оценки интервальные.

Точечная оценка параметров распределения

Пусть x₁, x₂, …, x_n – выборка объема n из генеральной совокупности с функцией распределения F(x).

Числовые характеристики этой выборки называются выборочными (эмпирическими) числовыми характеристиками.

Отметим, что выборочные числовые характеристики являются характеристиками данной выборки, но не являются характеристиками распределения генеральной совокупности. Однако эти характеристики можно использовать для оценок параметров генеральной совокупности.

Точечной называют статистическую оценку, которая определяется одним числом.

Точечная оценка характеризуется свойствами:несмещенность, состоятельность и эффективность.

Несмещенной называют точечную оценку, математическое ожидание которой равно оцениваемому параметру при любом объеме выборки.

Точечная оценка называется состоятельной, если при неограниченном увеличении объема выборки (n ® ¥) она сходится по вероятности к истинному значению параметра, то есть стремится к истинному значению оцениваемого параметра генеральной совокупности.

Эффективной называют точечную оценку, которая (при заданном объеме выборки n) имеет наименьшую возможную дисперсию, те есть гарантирует наименьшее отклонение выборочной оценки от такой же оценки генеральной совокупности..

В математической статистике показывается, что состоятельной, несмещенной оценкой генерального среднего значения а является выборочное средне:

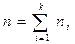
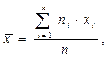
где х_i – варианта выборки, n_i – частота варианты х_i, – объем выборки.

Несмещенной оценкой генеральной дисперсии служит исправления выборочная дисперсия

,

Более удобна формула .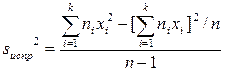

Оценка s 2 для генеральной дисперсии является также и состоятельной, но не является эффективной. Однако в случае нормального распределения она является «асимптотически эффективной», то есть при увеличении n отношение ее дисперсии к минимально возможной неограниченно приближается к единице.

Точечные оценки имеют тот недостаток, что при малом объеме выборки могут значительно отличаться от оцениваемых параметров. Поэтому, чтобы получить представление о близости между параметром и его оценкой, в математической статистике вводятся, так называемые, интервальные оценки.

Доверительный интервал

Если при статистической обработке результатов требуется найти не только точечную оценку неизвестного параметра θ, но и охарактеризовать точность этой оценки, то находится доверительный интервал.

Доверительный интервал – это интервал, в котором заранее заданной доверительной вероятностью находится неизвестный параметр генеральной совокупности.

Доверительная вероятность – это вероятность, с которой неизвестный параметр генеральной совокупности принадлежит доверительному интервалу.

Обычно принимают р = 0,95 или (реже) 0,99. Эти вероятности признаны достаточными для уверенного суждения о генеральных параметрах на основании известных выборочных показателей.

Доверительный интервал для математического ожидания имеет вид: где S – СКО, — критическое значение распределения Стьюдента (Смотри ПРИЛОЖЕНИЕ 1 к Теме 7)

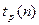
Доверительный интервал для дисперсии имеет вид

где 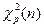— обратное распределение хи-квадрат (Смотри ПРИЛОЖЕНИЕ 2 к Теме 7)

ЗАДАЧА. Дана выборка 5, 6, 8, 2, 3, 1, 1, 4. Записать данные в виде вариационного ряда. Определить оценки среднего, дисперсии, и стандартного отклонения а также построить доверительные интервалы для среднего и дисперсии на уровне значимости a=0,05.

Решение. Представим данные в виде вариационного ряда: 1, 1, 2, 3, 4, 5, 6, 8. Так как n = 8, то выборочное среднее и исправленная выборочная дисперсия равны

Стандартное отклонение .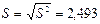

По таблицам из ПРИЛОЖЕНИЯ 1 и ПРИЛОЖЕНИЯ 2 к Теме 7. находим: ,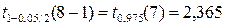

Получаем доверительный интервал для математического ожидания

или .

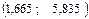
Доверительный интервал для дисперсии

или

Источник

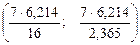
Точечные и интервальные оценки параметров распределения

Важной задачей математической статистики является задача оценивания (приближенного определения) по выборочным данным параметров закона распределения признака X генеральной совокупности. Другими словами, необходимо по данным выборочного распределения оценить неизвестные параметры теоретического распределения. Статистические оценки могут быть точечными и интервальными.

Задачу статистического оценивания, а также основные виды статистических оценок, рассмотрим для частного случая: пусть признак X генеральной совокупности распределен нормально, то есть теоретическое распределение имеет вид:

Точечной оценкой неизвестного параметра называют число (точку на числовой оси), которое приблизительно равно оцениваемому параметру и может заменить его с достаточной степенью точности в статистических расчетах.

Для того чтобы точечные статистические оценки обеспечивали хорошие приближения неизвестных параметров, они должны быть несмещенными, состоятельными и эффективными.

Состоятельной называют такую точечную статистическую оценку, которая при стремится по вероятности к оцениваемому параметру. В частности, если дисперсия несмещенной оценки при стремится к нулю, то такая оценка оказывается и состоятельной.

Эффективной называют такую точечную статистическую оценку, которая при фиксированном n имеет наименьшую дисперсию.

Вероятность того, что доверительный интервал заключает в себе (покрывает) неизвестный параметр равна и называется доверительной вероятностью или надежностью интервальной оценки. Величину называют точностью оценки.

Построим интервальную оценку параметра для двух случаев:

1) параметр нормального закона распределения признака Х генеральной совокупности известен. В этом случае интервальная оценка параметра с заданной надежностью определяется формулой:

2) параметр нормального закона распределения признака Х генеральной совокупности неизвестен. В этом случае интервальная оценка параметра с заданной надежностью определяется формулой:

Пример. С целью определения среднего трудового стажа на предприятии методом случайной повторной выборки проведено обследование трудового стажа рабочих. Из всего коллектива рабочих завода случайным образом выбрано 400 рабочих, данные о трудовом стаже которых и составили выборку. Средний по выборке стаж оказался равным 9,4 года. Считая, что трудовой стаж рабочих имеет нормальный закон распределения, определить с вероятностью 0,97 границы, в которых окажется средний трудовой стаж для всего коллектива, если известно, что = 1,7 года.

По таблице значений функции Лапласа из уравнения Ф(t) = 0,485 находим t = 2,17; тогда:

Источник