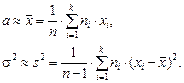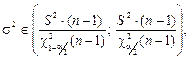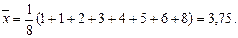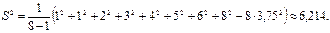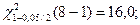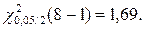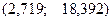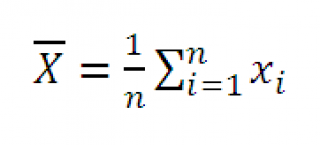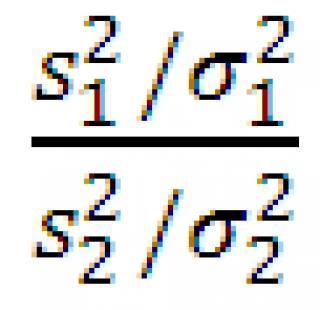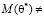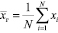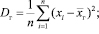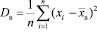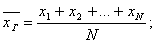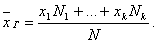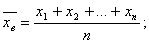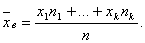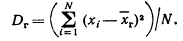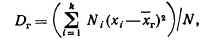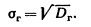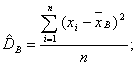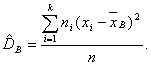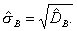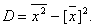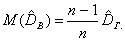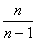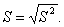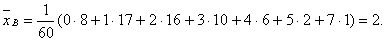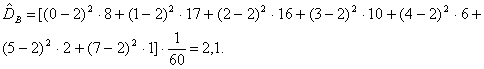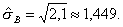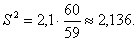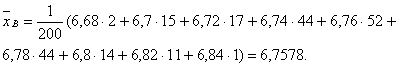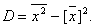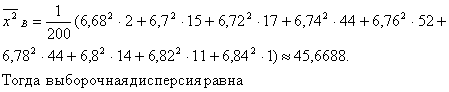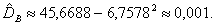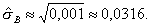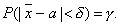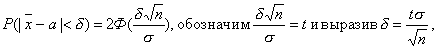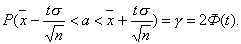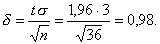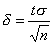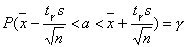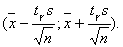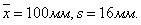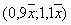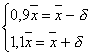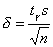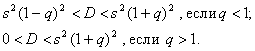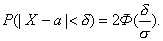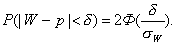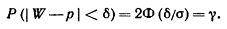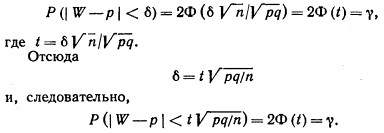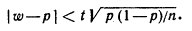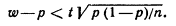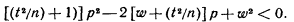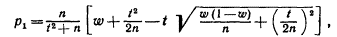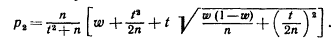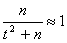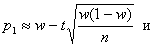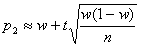точечные оценки параметров нормального распределения

Точечная оценка параметров распределения

Тема 7. Статистические оценки параметров распределения: точечные и интервальные оценки

Смысл статистических методов заключается в том, чтобы по выборке ограниченного объема, то есть по некоторой части генеральной совокупности, высказать обоснованное суждение о ее свойствах целиком.

Естественно, что замена исследования генеральной совокупно­сти исследованием выборки порождает ряд вопросов:

1. В какой степени выборка отражает свойства генеральной совокупности, т. е. в какой степени выборка репрезентативна по отношению к генеральной совокупности?

2. Какую информацию о значениях параметров генеральной совокупности могут дать параметры выборки?

3. Можно ли утверждать, что полученные выборочным путем статистические характеристики (средние величины, дисперсия или любые другие производные величины) равны тем характе­ристикам, которые могут быть получены из генеральной сово­купности.

Проверка показывает, что значения параметров, полученных для разных выборок из одной генеральной совокупности, обыч­но не совпадают. Рассчитанные выборочным путем числовые значения параметров выборок являются лишь результатом при­ближенного статистического оценивания значений этих парамет­ров в генеральной совокупности. Статистическое оценивание, в силу изменчивости наблюдаемых явлений, позволяет получать только их приближенные значения.

Примечание. Строго говоря, в статистике оценка — это правило вычисления оцениваемого параметра, а термин оценить, т. е. провести оценивание, означает указать приближенное значе­ние.

Различают оценки точечные и оценки интервальные.

Точечная оценка параметров распределения

Пусть x₁, x₂, …, x_n – выборка объема n из генеральной совокупности с функцией распределения F(x).

Числовые характеристики этой выборки называются выборочными (эмпирическими) числовыми характеристиками.

Отметим, что выборочные числовые характеристики являются характеристиками данной выборки, но не являются характеристиками распределения генеральной совокупности. Однако эти характеристики можно использовать для оценок параметров генеральной совокупности.

Точечной называют статистическую оценку, которая определяется одним числом.

Точечная оценка характеризуется свойствами:несмещенность, состоятельность и эффективность.

Несмещенной называют точечную оценку, математическое ожидание которой равно оцениваемому параметру при любом объеме выборки.

Точечная оценка называется состоятельной, если при неограниченном увеличении объема выборки (n ® ¥) она сходится по вероятности к истинному значению параметра, то есть стремится к истинному значению оцениваемого параметра генеральной совокупности.

Эффективной называют точечную оценку, которая (при заданном объеме выборки n) имеет наименьшую возможную дисперсию, те есть гарантирует наименьшее отклонение выборочной оценки от такой же оценки генеральной совокупности..

В математической статистике показывается, что состоятельной, несмещенной оценкой генерального среднего значения а является выборочное средне:

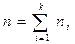
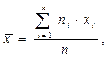
где х_i – варианта выборки, n_i – частота варианты х_i, – объем выборки.

Несмещенной оценкой генеральной дисперсии служит исправления выборочная дисперсия

,

Более удобна формула .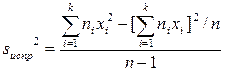

Оценка s 2 для генеральной дисперсии является также и состоятельной, но не является эффективной. Однако в случае нормального распределения она является «асимптотически эффективной», то есть при увеличении n отношение ее дисперсии к минимально возможной неограниченно приближается к единице.

Точечные оценки имеют тот недостаток, что при малом объеме выборки могут значительно отличаться от оцениваемых параметров. Поэтому, чтобы получить представление о близости между параметром и его оценкой, в математической статистике вводятся, так называемые, интервальные оценки.

Доверительный интервал

Если при статистической обработке результатов требуется найти не только точечную оценку неизвестного параметра θ, но и охарактеризовать точность этой оценки, то находится доверительный интервал.

Доверительный интервал – это интервал, в котором заранее заданной доверительной вероятностью находится неизвестный параметр генеральной совокупности.

Доверительная вероятность – это вероятность, с которой неизвестный параметр генеральной совокупности принадлежит доверительному интервалу.

Обычно принимают р = 0,95 или (реже) 0,99. Эти вероятности признаны достаточными для уверенного суждения о генеральных параметрах на основании известных выборочных показателей.

Доверительный интервал для математического ожидания имеет вид: где S – СКО, — критическое значение распределения Стьюдента (Смотри ПРИЛОЖЕНИЕ 1 к Теме 7)

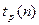
Доверительный интервал для дисперсии имеет вид

где 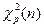— обратное распределение хи-квадрат (Смотри ПРИЛОЖЕНИЕ 2 к Теме 7)

ЗАДАЧА. Дана выборка 5, 6, 8, 2, 3, 1, 1, 4. Записать данные в виде вариационного ряда. Определить оценки среднего, дисперсии, и стандартного отклонения а также построить доверительные интервалы для среднего и дисперсии на уровне значимости a=0,05.

Решение. Представим данные в виде вариационного ряда: 1, 1, 2, 3, 4, 5, 6, 8. Так как n = 8, то выборочное среднее и исправленная выборочная дисперсия равны

Стандартное отклонение .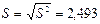

По таблицам из ПРИЛОЖЕНИЯ 1 и ПРИЛОЖЕНИЯ 2 к Теме 7. находим: ,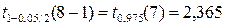

Получаем доверительный интервал для математического ожидания

или .

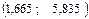
Доверительный интервал для дисперсии

или

Источник

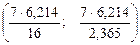
Точечные оценки параметров нормального распределения.

Пусть случайная величина Xимеет нормальное распределение: Хе N (а, о). Параметры а, о нормального распределения, как правило, неизвестны. С целью их определения производится эксперимент, в результате которого фиксируется п значений случайной величины X: Xi,X₂,

Вообще говоря, по результатам выборки, какого бы большого размера она ни была, нельзя определить точные значения неизвестных параметров а и о, но можно найти их приближенные значения а, а, которые называются оценками.

Для нахождения приближенных значений а, а неизвестных параметров а и о нормального закона, будем рассматривать функции вида: а = а<х_<, х₂. х_п), а = o(x_l5 х₂. х_п), которые называются выборочными функциями или статистиками.

Задача оценки неизвестных параметров а и а сводится к нахождению таких статистик й, а, которые могут быть использованы для приближенного определения значений неизвестных параметров аио.

Оценки параметров подразделяются на точечные и интервальные.

Интервальной оценкой называют оценку, которая определяется двумя числами 0j и 0₂ — концами интервала, накрывающего оцениваемый параметр 0.

Можно показать, что если случайная величина X е N (а, а), то точечные оценки неизвестных параметров оио находятся по формулам (4.10) и (4.11):

Эти оценки обладают свойствами несмещенности, состоятельности и эффективности.

Интервальные оценки параметров нормального распределения.

Пусть X eN (а, а), причем я и о неизвестны. Для нахождения точечных оценок а и а из генеральной совокупности извлечена выборка объемом п. Пусть на основании этой выборки найдены точечные несмещенные оценки неизвестных параметров а и о по формулам (4.10) и (4.11). Точечные оценки, найденные по выборке объемом п, не позволяют непосредственно ответить на вопрос, какая ошибка допущена, если вместо точного значения неизвестного параметра а или а принимаются его приближенные значения а, а.

Поэтому во многих случаях выгоднее пользоваться интервальной оценкой, основанной на определении некоторого интервала, внутри которого с определенной вероятностью находится неизвестное значение параметра а (или а).

лучше качество оценки, тем она точнее. Таким образом, положительное число е характеризует точность оценки:

точечной оценки математического ожидания.

Квантили стандартизованного нормального распределения приведены в таблицах приложения 7.

Анализируя формулу доверительного интервала, задаваемого системой неравенств (4.15), можно заметить, что:

выборки, который обеспечивает заданную точность.

Если же о неизвестно, тогда доверительный интервал, накрывающий неизвестное математическое ожидание а случайной величины XeN(а, а), имеет следующий вид:

где t_a — квантиль распределения Стьюдента, определяемый

ления; е = t_a —j= — предельная погрешность точечного оцени- 2 V п

вания математического ожидания СВXeN(а, о) при неизвестном о обладает теми же свойствами, что и при известном а.

Доверительный интервал для среднеквадратического отклонения о задается системой неравенств

Значение величин = —-и y₂ = —-приведены в таб-

Источник

Статистики, их выборочные распределения и точечные оценки параметров распределений в EXCEL

history 26 ноября 2016 г.

В статье напомним некоторые понятия математической статистики: выборка, статистика, точечная оценка, выборочное распределение. Продемонстрируем в MS EXCEL сходимость некоторых распределений статистик к нормальному распределению, распределению ХИ-квадрат, распределению Стьюдента и F — распределению.

Сначала напомним основные понятия математической статистики, необходимые для оценки параметров.

О выборке

После того, как выборка была получена, следующим вопросом является то, каким образом получить информацию о неизвестном распределении:

Примечание : Для некоторых распределений дисперсия и стандартное отклонение случайной величинымогут быть одновременно показателями и параметрами распределения (например, для нормального распределения ).

О статистиках и точечной оценке параметров распределения

Примечание : Про оценку параметров конкретного распределения можно прочитать в статье, относящейся к этому распределению (см. заглавную статью о распределениях ).

Выборочные распределения статистик

Выборочное распределение среднего

Пусть выборка извлекается из нормального распределения с параметрами N(μ;σ 2 ). Рассмотрим статистику Х _ср ( среднее выборки ):

Из Центральной предельной теоремы известно, что выборочное распределение статистики Х _ср ( выборочное распределение среднего ) при достаточно большом размере выборки n стремится к нормальному распределению с параметрами N(μ;σ 2 /n).

Проверим это утверждение в MS EXCEL (см. файл примера Лист Нормальное ). Для этого возьмем 60 значений выборочных средних (Хср), вычисленныхна основе 60 случайных выборок, взятых из нормального распределения с параметрами N(μ;σ 2 ). Размер выборки n взят равным 50.

Как видно из рисунка выше, средние значения выборок хорошо укладываются на прямой, что позволяет сделать вывод о нормальности распределения. Параметры этого распределения можно, например, с помощью линии регрессии, которые близки к расчетным.

Выборочное распределение статистики

Известно, что выборочное распределение статистики при достаточно большом размере выборки стремится к распределению Стьюдента с n-1 степенью свободы.

Выборочное распределение статистики (n-1)s 2 /σ 2

Известно, что Выборочное распределение статистики (n-1)s 2 /σ 2 при достаточно большом размере выборки стремится к распределению ХИ-квадрат с n-1 степенью свободы.

Выборочное распределение статистики

Пусть из двух нормальных распределений с параметрами N(μ ₁ ;σ ₁ 2 ) и N(μ ₂ ;σ ₂ 2 ) извлекается по одной выборке (в общем случае разного размера n ₁ и n ₂ ) .

В файле примера на листе F-расп построен График вероятности для проверки этого утверждения.

Источник

Точечные оценки параметров нормального распределения

Методы математической статистики используются при анализе явлений, которые обладают свойством статистической устойчивости. Сущность данного свойства заключается в том, что результат Х определённого опыта не может быть предсказан с большой точностью, где значение функции 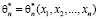от результатов наблюдений при увеличении объёма выборки теряет своё свойство случайности и сходится по вероятности с неслучайной величиной θ [9].

В математической статистике применяются следующие оценки [3, 7]:

– несмещённые (значение математического ожидания оценки совпадает со значением оценивающего параметра, то есть );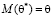

– смещённые (оценка );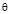

– эффективные (оценка, которая имеет при заданном объёме выборки n наименьшую дисперсию);

– состоятельные (оценка, которая стремится при 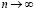по вероятности к оцениваемому параметру);

Точечной оценкой называют некоторую функцию результатов наблюдения 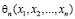, значение которой принимается за более приближенное в данных условиях к значению самого параметра θ, то есть оценку, определяющую одним числом [5, 2].

Часто, по результатам наблюдений количественного признака X требуется оценить следующие параметры распределения генеральной совокупности:

– генеральная средняя M(X);

– генеральная дисперсия D(X);

В качестве точечных оценок этих параметров выступают выборочная средняя и выборочная дисперсия 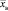и Dв соответственно [1, 4].

Генеральная средняя – среднее арифметическое значений генеральной совокупности :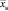

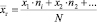
– с повторениями

Выборочная средняя – среднее арифметическое значение выборки [3, 8].

То есть, имеется выборка объёма n, тогда выборочная средняя равна:

.

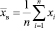
Выборочная средняя по данным одной выборки является определённым числом. Также выборочная средняя является несмещённой оценкой математического ожидания.

При увеличении объёма выборки n вся выборочная система стремится к генеральной средней [6, 9].

Генеральной дисперсией называют среднеарифметическое квадратное отклонение значений генеральной совокупности от их среднего значения.

Кроме дисперсий для характеристики рассеивания значений генеральной совокупности вокруг своего среднего также можно пользоваться средним квадратическим отклонением [10].

Выборочная дисперсия – среднее арифметическое квадратов отклонений, наблюдаемых значений выборки от их среднего значения.

Справедлива также формула:

.

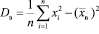
Для исправления выборочной дисперсии необходимо умножить её на дробь:

.

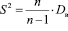
Получаем исправленную выборочную дисперсию, которая является несмещённой оценкой генеральной дисперсии.

– с повторениями.

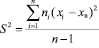
Для оценки рассеивания выборки служит выборочное среднеквадратическое отклонение.

Теперь рассмотрим, как применяются перечисленные данные при решении задач.

Из генеральной совокупности извлечена выборка объёма n=30;

Источник

Точечные оценки параметров нормального распределения

2.1. Интервальные оценки параметров нормального распределения.

Пусть требуется изучить количественный признак генеральной совокупности. Допустим, что из теоретических соображений удалось установить, какое именно распределение имеет признак. Возникает задача оценки параметров, которыми определяется это распределение.

Итак, статистической оценкой неизвестного параметра теоретического распределения называют функцию от наблюдаемых случайных величин.

Для того чтобы статистические оценки давали «хорошие» приближения оцениваемых параметров, они должны удовлетворять определенным требованиям: оценка должна быть несмещенной, эффективной и состоятельной.

Поясним каждое из понятий.

Смещенной называют оценку, математическое ожидание которой не равно оцениваемому параметру.

Эффективной называют статистическую оценку, которая (при заданном объеме выборки п) имеет наименьшую возможную дисперсию.

При рассмотрении выборок большого объема ( n велико!) к статистическим оценкам предъявляется требование состоятельности.

Состоятельной называют статистическую оценку, которая при п ®¥ стремится по вероятности к оцениваемому параметру. Например, если дисперсия несмещенной оценки при п ®¥ стремится к нулю, то такая оценка оказывается и состоятельной.

Рассмотрим точечные оценки параметров распределения, т.е.

Пусть изучается генеральная совокупность относительно количественного признака Х.

Генеральной средней называют среднее арифметическое значений признака генеральной совокупности.

Если все значения признака различны, то

Выборочной средней называют среднее арифметическое значение признака выборочной совокупности.

Если все значения признака выборки различны, то

Выборочная средняя является несмещенной и состоятельной оценкой генеральной средней.

Замечание: Если выборка представлена интервальным вариационным рядом, то за x_i принимают середины частичных интервалов.

Для того чтобы охарактеризовать рассеяние значений количественного признака Х генеральной совокупности вокруг своего среднего значения, вводят сводную характеристику — генеральную дисперсию.

Если все значения признака генеральной совокупности объема N различны, то

Кроме дисперсии для характеристики рассеяния зна­чений признака генеральной совокупности вокруг своего среднего значения пользуются сводной характеристикой— средним квадратическим отклонением.

Генеральным средним квадратическим отклонением (стандартом) называют квадратный корень из генеральной дисперсии:

Если все значения признака выборки различны, то

Выборочным средним квадратическим отклоненим называют квадратный корень из выборочной дисперсии:

Вычисление дисперсии- выборочной или генеральной, можно упростить, используя формулу:

Замечание: если выборка представлена интервальным вариационным рядом, то за x_i принимают середины частичных интервалов.

Выборочная дисперсия является смещенной оценкой генеральной дисперсии, т.е. математическое ожидание выборочной дисперсии не равно оцениваемой генеральной дисперсии, а равно

Для исправления выборочной дисперсии достаточно умножить ее на дробь

В качестве оценки генеральной дисперсии принимают исправленную дисперсию.

Для оценки среднего квадратического генеральной совокупности используют исправленное среднее квадратическое отклонение

Замечание: формулы для вычисления выборочной дисперсии и исправленной дисперсии отличаются только знаменателями. При достаточно больших n выборочная и исправленная дисперсии мало отличаются, поэтому на практике исправленной дисперсией пользуются, если n

Пример 1. Для дискретного вариационного ряда:

Выборочное среднее квадратическое отклонение

Пример2. Для интервального вариационного ряда:

За х _i примем середины частичных интервалов:

_{Д ля вычисления выборочной дисперсии воспользуемся формулой}

Выборочное среднее квадратическое отклонение :

Таким образом, положительное число d характеризует точность оценки.

Обычно надежность оценки задается наперед, причем в качестве g берут число, близкое к единице. Наиболее часто задают надежность, равную 0,95; 0,99 и 0,999.

Пусть вероятность того, что, |Q- Q*| d равна g :

Заменив неравенство равносильным ему двойным неравенством получим:

Потребуем, чтобы выполнялось равенство

Задача решена. Число t находят по таблице функции Лапласа Ф(х).

Пример1. СВХ распределена нормально и s =3. Найти доверительный интервал для оценки математического ожидания по выборочным средним, если n = 36 и задана надежность g =0,95.

Пример2. Найти минимальный объем выборки, который обеспечивает заданную точность d =0,3 и надежность g = 0,975, если СВХ распределена нормально и s =1,2.

подставим значения и получим минимльный объем выборки n

Т.к. мы не знакомы с законами распределения СВ, которые используются при выводе формулы, то примем ее без доказательства.

и доверительный интервал имеет вид

Пример1. Найти доверительный интервал для оценки математического ожидания с надежностью 0,95, если объем выборки n =16, среднее выборочное и исправленная дисперсия соответственно равны 20,2 и 0,8.

откуда получим доверительный интервал (19,774; 20,626)

Смысл полученного результата: если взять 100 различных выборок, то в 95 из них математическое ожидание будет находится в пределах данного интервала, а в 5 из них- нет.

Пример2. Измеряют диаметры 25 корпусов электродвигателей. Получены выборочные характеристики

Необходимо найти вероятность (надежность) того, что

— является доверительным интервалом оценки математического ожидания при нормальном распределении.

Откуда d =10. Из равенства

откуда t _g =3,125. По таблице для найденного t _g и n = 25 находим g =0,99.

Потребуем выполнения соотношения

Раскроем модуль и получим двойное неравенство:

Пример1. По выборке объема n = 25 найдено «исправленное» среднее квадратическое отклонение s = 0,8. Найти доверительный интервал, покрывающий генеральное среднее квадратическое отклонение с надежностью 0,95.

Искомый доверительный интервал 0,8(1- 0,32) s 0,8(1+ 0,32) или 0,544 s 0,056.

Пример2. По выборке объема n = 10 найдено s = 0,16. Найти доверительный интервал, покрывающий генеральное среднее квадратическое отклонение с надежностью 0,999.

q ( n =10, g =0,999) = 1,8>0.

Искомый доверительный интервал 0 s 0,16(1+1,8) или 0 s

Найдем доверительный интервал для оценки вероятности по относительной частоте, используя формулу:

Приступим к построению доверительного интервала (р₁, р₂), который с надежностью g покрывает оцениваемый параметр р Потребуем, чтобы с надежностью g выполнялось соотношение указанное выше равенство:

Таким образом, с надежностью g выполняется неравенство (чтобы получить рабочую формулу, случайную величину W заменим неслучайной наблюдаемой относительной частотой w и подставим 1- р вместо q ):

Учитывая, что вероятность р неизвестна, решим это неравенство относительно р. Допустим, что w > р. Тогда

Обе части неравенства положительны; возведя их в квадрат, получим равносильное квадратное неравенство относительно р:

Дискриминант трехчлена положительный, поэтому корни действительные и различные:

,и

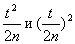
получим приближенные формулы для границ доверительного интервала :

Пример1. Производят независимые испытания с одинаковой и неизвестной вероятностью появления события А в каждом испытании. Найти доверительный интервал для оценки вероятности с надежностью 0,95, если в 80 испытаниях событие А появилось 16 раз.

По условию n =80, m =16, g =0,95. Относительная частота

Из соотношения Ф( t )=0,95/2 = 0,475 по таблице находим t = 1,96. Т.к. n то используем точные формулы, получим : р₁= 0,128, р₂= 0,299.

Пример. В пяти независимых испытаниях событие А произошло 3 раза. Найти с надежностью 0,95 интервальную оценку для вероятности события А в единичном испытании.

По условию задачи n =5, m =3. Имеет место схема повторных испытаний. Используя таблицу, находим доверительный интервал : 0,147 p

1. Определение статистической оценки неизвестного параметра.

2. Какая оценка называется точечной?

3. Каким требованиям должны удовлетворять статистические оценки?

4. Сформулировать определения генеральной средней и генеральной дисперсии.

5. Записать выражения для вычисления выборочной средней, выборочной дисперсии и исправленной дисперсии. Какая из этих оценок не является несмещенной?

7. Методика вычисления границ доверительного интервала для оценки среднего квадратического отклонения нормально распределенной СВ.

Источник