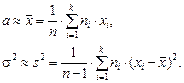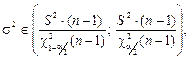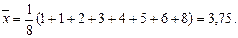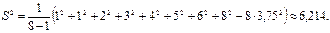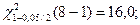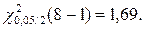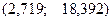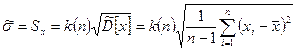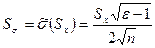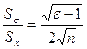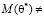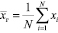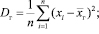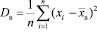точечные оценки параметров распределения случайной величины

Точечные оценки параметров распределения случайных величин и отклонений

Вероятностные характеристики погрешностей измерения определяются, как правило, на основании экспериментальных данных методами математической статистики. Иногда для этого проводят специальные эксперименты с целью аттестации средств измерения, иногда они совмещены с измерениями контролируемого параметра. При этом оцениваются математическое ожидание и среднее квадратичное отклонение.

Оценка вероятностной характеристики погрешностей измерения называется точечной, если она выражена одним числом. Любая точечная оценка, вычисленная на основании опытных данных, является случайной величиной. При этом функция ее распределения зависит от распределения случайной величины и числа опытов п.

Точечная оценка называется несмещенной, если ее математическое ожидание совпадает с истинным значением оцениваемого параметра.

Точечная оценка называется состоятельной, если при увеличении количества наблюдений (объема выборки) ее отличие от оцениваемого параметра может быть сколь угодно малым.

Точечная оценка называется эффективной, если ее дисперсия меньше дисперсии любой другой оценки данного параметра.

Каждое из этих понятий характеризует качество точечных оценок. При прочих равных условиях лучшей будет та оценка, которая имеет, например, наименьшее смешение. Среди всех нормально распределенных оценок наилучшей будет несмещенная эффективная оценка.

Теоретическим обоснованием возможности экспериментального определения вероятностных характеристик является закон больших чисел, который для случайных величин формулируется следующим образом.

Пусть проведена серия и одинаковых независимых экспериментов по наблюдению за случайной величиной X, имеющей конечные М(х) и /)(а).

Обозначим через X среднее арифметическое результатов наблюдений

В соответствии с законом больших чисел для любых сколь угодно малых £и а всегда найдется такое при котором в случае п > и, ь4

Среднее арифметическое результатов наблюдений является несмещенной оценкой математического ожидания случайной величины, а следовательно, ее истинное значение совпадаете математическим ожиданием случайной величины:

Из выражения (5.56) следует, что точность результата измерения можно повысить при увеличении числа измерений. Дисперсия среднего арифметического из п наблюдений в п раз меньше дисперсии результата однократного наблюдения.

Среднее квадратичное отклонение среднего арифметического определяется по формуле

Среднее арифметическое значение является также и эффективной оценкой математического ожидания, т. е. имеет минимальную дисперсию, равную £1^1.

Рассмотрим пример определения среднего арифметического на основании изменяющегося числа наблюдений.

Рис. 5.13. Зависимость результатов наблюдений от числа наблюдений

Среднее из 20 наблюдений А1 =1,75 мкм служит точечной оценкой истинного отклонения измеряемой величины.

Результаты отдельных измерений, как это следует из графика, имеют достаточно большой разброс относительно среднего арифметического (ряд I), а разброс отдельных средних арифметических значительно меньше (ряд 2). Он уменьшается по мере увеличения числа измерений.

В качестве точечной оценки дисперсии выбирают среднее значение квадрата отклонения случайной величины от среднего значения

Эта оценка является состоятельной, но смешенной, так как ее математическое ожидание равно

В связи с этим точечную оценку дисперсии принято определять по формуле:

Точечная оценка среднего квадратичного отклонения определяется из выражения

Величина ^характеризует разброс отдельных результатов измерения относительно среднего арифметического значения X.

Среднее арифметическое X имеет дисперсию, в п раз меньшую, чем дисперсия случайной погрешности (5.57). В связи с этим в качестве точечной оценки дисперсии среднего арифметического принимается выражение

Оценка среднего квадратичного отклонения среднего арифметического соответственно равна

что позволяет сделать соответствующие выводы относительно точности измерения: число измерений п характеризует надежность определения л*» а величина л;( характеризует близость А1 к истинному значению Л.

Источник

Точечная оценка параметров распределения

Тема 7. Статистические оценки параметров распределения: точечные и интервальные оценки

Смысл статистических методов заключается в том, чтобы по выборке ограниченного объема, то есть по некоторой части генеральной совокупности, высказать обоснованное суждение о ее свойствах целиком.

Естественно, что замена исследования генеральной совокупно­сти исследованием выборки порождает ряд вопросов:

1. В какой степени выборка отражает свойства генеральной совокупности, т. е. в какой степени выборка репрезентативна по отношению к генеральной совокупности?

2. Какую информацию о значениях параметров генеральной совокупности могут дать параметры выборки?

3. Можно ли утверждать, что полученные выборочным путем статистические характеристики (средние величины, дисперсия или любые другие производные величины) равны тем характе­ристикам, которые могут быть получены из генеральной сово­купности.

Проверка показывает, что значения параметров, полученных для разных выборок из одной генеральной совокупности, обыч­но не совпадают. Рассчитанные выборочным путем числовые значения параметров выборок являются лишь результатом при­ближенного статистического оценивания значений этих парамет­ров в генеральной совокупности. Статистическое оценивание, в силу изменчивости наблюдаемых явлений, позволяет получать только их приближенные значения.

Примечание. Строго говоря, в статистике оценка — это правило вычисления оцениваемого параметра, а термин оценить, т. е. провести оценивание, означает указать приближенное значе­ние.

Различают оценки точечные и оценки интервальные.

Точечная оценка параметров распределения

Пусть x₁, x₂, …, x_n – выборка объема n из генеральной совокупности с функцией распределения F(x).

Числовые характеристики этой выборки называются выборочными (эмпирическими) числовыми характеристиками.

Отметим, что выборочные числовые характеристики являются характеристиками данной выборки, но не являются характеристиками распределения генеральной совокупности. Однако эти характеристики можно использовать для оценок параметров генеральной совокупности.

Точечной называют статистическую оценку, которая определяется одним числом.

Точечная оценка характеризуется свойствами:несмещенность, состоятельность и эффективность.

Несмещенной называют точечную оценку, математическое ожидание которой равно оцениваемому параметру при любом объеме выборки.

Точечная оценка называется состоятельной, если при неограниченном увеличении объема выборки (n ® ¥) она сходится по вероятности к истинному значению параметра, то есть стремится к истинному значению оцениваемого параметра генеральной совокупности.

Эффективной называют точечную оценку, которая (при заданном объеме выборки n) имеет наименьшую возможную дисперсию, те есть гарантирует наименьшее отклонение выборочной оценки от такой же оценки генеральной совокупности..

В математической статистике показывается, что состоятельной, несмещенной оценкой генерального среднего значения а является выборочное средне:

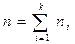
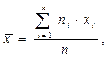
где х_i – варианта выборки, n_i – частота варианты х_i, – объем выборки.

Несмещенной оценкой генеральной дисперсии служит исправления выборочная дисперсия

,

Более удобна формула .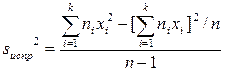

Оценка s 2 для генеральной дисперсии является также и состоятельной, но не является эффективной. Однако в случае нормального распределения она является «асимптотически эффективной», то есть при увеличении n отношение ее дисперсии к минимально возможной неограниченно приближается к единице.

Точечные оценки имеют тот недостаток, что при малом объеме выборки могут значительно отличаться от оцениваемых параметров. Поэтому, чтобы получить представление о близости между параметром и его оценкой, в математической статистике вводятся, так называемые, интервальные оценки.

Доверительный интервал

Если при статистической обработке результатов требуется найти не только точечную оценку неизвестного параметра θ, но и охарактеризовать точность этой оценки, то находится доверительный интервал.

Доверительный интервал – это интервал, в котором заранее заданной доверительной вероятностью находится неизвестный параметр генеральной совокупности.

Доверительная вероятность – это вероятность, с которой неизвестный параметр генеральной совокупности принадлежит доверительному интервалу.

Обычно принимают р = 0,95 или (реже) 0,99. Эти вероятности признаны достаточными для уверенного суждения о генеральных параметрах на основании известных выборочных показателей.

Доверительный интервал для математического ожидания имеет вид: где S – СКО, — критическое значение распределения Стьюдента (Смотри ПРИЛОЖЕНИЕ 1 к Теме 7)

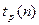
Доверительный интервал для дисперсии имеет вид

где 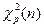— обратное распределение хи-квадрат (Смотри ПРИЛОЖЕНИЕ 2 к Теме 7)

ЗАДАЧА. Дана выборка 5, 6, 8, 2, 3, 1, 1, 4. Записать данные в виде вариационного ряда. Определить оценки среднего, дисперсии, и стандартного отклонения а также построить доверительные интервалы для среднего и дисперсии на уровне значимости a=0,05.

Решение. Представим данные в виде вариационного ряда: 1, 1, 2, 3, 4, 5, 6, 8. Так как n = 8, то выборочное среднее и исправленная выборочная дисперсия равны

Стандартное отклонение .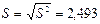

По таблицам из ПРИЛОЖЕНИЯ 1 и ПРИЛОЖЕНИЯ 2 к Теме 7. находим: ,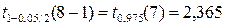

Получаем доверительный интервал для математического ожидания

или .

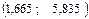
Доверительный интервал для дисперсии

или

Источник

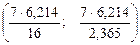
Точечные оценки параматров распределения

Мы подошли к решению вопроса о том, как на основании полученной в эксперименте группы результатов наблюдений оценить истинное значение, т.е. найти результат измерений, как оценить его точность, т.е. меру его приближения к истинному значению.

Рассмотренные в рамках предыдущей лекции функции распределения описывают пове­дение непрерывных случайных величин, т.е. величин, возможные значения которых неотделимы друг от друга и непрерывно запол­няют некоторый конечный или бесконечный интервал. На прак­тике все результаты измерений и случайные погрешности являют­ся величинами дискретными, т.е. величинами x_i возможные зна­чения которых отделимы друг от друга и поддаются счету.

При использовании дискретных случайных величин возникает задача нахождения точечных оценок параметров их функций распределе­ния на основании выборок – ряда значений х_i принимаемых слу­чайной величиной х в n независимых опытах. Используемая вы­борка должна быть репрезентативной (представительной), т.е. должна достаточно хорошо представлять пропорции генеральной совокупности.

Оценка параметра называется точечной, если она выражается одним числом. Задача нахождения точечных оценок – частный случай статистической задачи нахождения оценок параметров функции распределения случайной величины на основании выбор­ки. Любая точечная оценка, вычисленная на основании опытных данных, является их функцией и поэтому сама должна представлять собой случайную величину с распределением, зависящим от распределения исходной случайной величины, в том числе от самого оцениваемого параметра и от числа опытов n.

Состоятельной называется оценка, которая при увеличении объема выборки стремится по вероятности к ис­тинному значению числовой характеристики.

Несмещенной на­зывается оценка, математическое ожидание которой равно оце­ниваемой числовой характеристике (параметру).

Оценка называется эффективной, если ее дисперсия меньше дисперсии любой другой оценки данного параметра, т.е. наиболее эффективной счи­тают ту из нескольких возможных несмещенных оценок, которая имеет наименьшую дисперсию.

Требование несмещенности на прак­тике не всегда целесообразно, так как оценка с небольшим сме­щением и малой дисперсией может оказаться предпочтительнее несмещенной оценки с большой дисперсией. На практике не все­гда удается удовлетворить одновременно все три этих требова­ния, однако выбору оценки должен предшествовать ее критиче­ский анализ со всех перечисленных точек зрения.

Наиболее распространенным методом получения оценок явля­ется, метод наибольшего (максимального) правдоподобия, теоретически обоснованный математиком Р. Фишером, который приводит к асимптотически несмещенным и эффективным оценкам с при­ближенно нормальным распределением. Среди других методов мож­но назвать методы моментов и наименьших квадратов.

Точечной оценкой математического ожидания результата измерений является среднее арифметическое значение измеряемой величины:

(6.1)

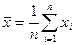
При любом законе распределения оно является состоятельной и несмещенной оценкой, а также наиболее эффективной по крите­рию наименьших квадратов.

Точечная оценка дисперсии, определяемая по формуле:

(6.2)

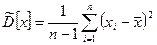
является несмещенной и состоятельной.

Среднеквадратическое отклонение случайной величины х определяется как корень квадрат­ный из дисперсии. Соответственно его оценка может быть найдена путем извлечения корня из оценки дисперсии. Однако эта опера­ция является нелинейной процедурой, приводящей к смещенности получаемой таким образом оценки. Для исправления оценки СКО вводят поправочный множитель k(n), зависящий от числа наблю­дений n.

Он изменяется от k(3) = 1,13 до k(∞) = 1,03. Оценка сред­него квадратического отклонения:

(6.3)

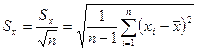
Оценка СКО среднего квадратического отклонения:

Отсюда следует, что относительная погрешность определения СКО может быть оценена как:

Она зависит только от эксцесса и числа наблюдений в выборке и не зависит от СКО, т.е. той точности, с которой производятся измерения. Ввиду того, что большое число измерений проводит­ся относительно редко, погрешность определения, а может быть весьма существенной. В любом случае она больше погрешности из-за смещенности оценки, обусловленной извлечением квадрат­ного корня и устраняемой поправочным множителем k(n).

В связи с этим на практике пренебрегают учетом смещенности оценки СКО отдельных наблюдений и определяют его по формуле:

(6.4)

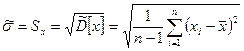
Иногда оказывается удобнее использовать следующие формулы для расчета оценок СКО отдельных наблюдений и результата измерения:

; (6.5)

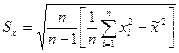
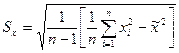
Точечные оценки других параметров распределений использу­ются значительно реже.

Оценки коэффициента асимметрии и экс­цесса находятся по формулам:

; (6.6)

(6.7)

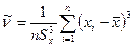
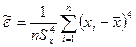
Определение рассеяния оценок коэффициента асимметрии и экс­цесса описывается различными формулами в зависимости от вида распределения.

Источник

Точечные оценки параметров случайной величины

Точечными оценками параметров называют такие оценки, которые выражаются каким-то одним числом (точкой). Таким числом может быть, например, параметр X закона Пуассона или параметры а и а нормального распределения. Не все переменные могут быть оценками.

Рассмотрим наиболее важные требования, которым должна удовлетворять оценка параметра генеральной совокупности.

1. Несмещенность. Оценка не должна содержать систематической ошибки. Это означает, что математическое ожидание оценки некоторого параметра, взятое по всем возможным выборкам, должно быть равно действительному значению параметра.

Если действительное значение оцениваемого параметра обозначить а₀, а его оценку а, то требование несмещенности запишется в виде

Если это требование не выполняется, то в среднем оценка а будет всегда давать значение а₀ с некоторым отклонением.

2. Состоятельность. Оценка а должна приближаться к а₀ по мере увеличения объема выборки. Но ввиду того, что оценка а является случайной величиной, об этом приближении можно говорить только в вероятностном смысле.

Для состоятельности оценки а, получаемой при выборке объема п, должно выполняться условие сходимости по вероятности а к а₀

3. Эффективность. Из всех несмещенных и состоятельных оценок следует предпочесть такую, при которой большие отклонения при использовании различных выборок встречались бы как можно реже. Оценкой эффективности несмещенной оценки является ее дисперсия.

Математически требование эффективности означает требование минимальной дисперсии оценки

Рассмотрим несмещенные точечные оценки параметров распределения. Запишем в виде таблицы полученные в результате изучения выборки значения признака X в неубывающем порядке х_г 2 определяется по формуле

или по упрощенной формуле

где х 2 определяется по формуле

В качестве точечной оценки параметров генеральной совокупности может приниматься соответствующий параметр выборки.

Можно доказать, что:

1) х является несмещенной точечной оценкой х₀, т.е.

2) оценка а 2 для генеральной дисперсии является состоятельной, но смещенной. Поэтому вводят величину

которая называется исправленной статистической выборочной дисперсией. s 2 является несмещенной оценкой генеральной дисперсии т.е. M(s 2 ) = o(j.

Величина s = Vs 2 называется исправленным выборочным средним квадратическим отклонением и является несмещенной точечной оценкой генерального среднего квадратичного отклонения ст₀, т.е.

В следственном изоляторе проводилось измерение физических параметров заключенных, в частности приведены результаты измерения роста в сантиметрах у 100 случайно отобранных заключенных.

Источник

Точечные оценки параметров распределения случайной величины

Методы математической статистики используются при анализе явлений, которые обладают свойством статистической устойчивости. Сущность данного свойства заключается в том, что результат Х определённого опыта не может быть предсказан с большой точностью, где значение функции 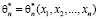от результатов наблюдений при увеличении объёма выборки теряет своё свойство случайности и сходится по вероятности с неслучайной величиной θ [9].

В математической статистике применяются следующие оценки [3, 7]:

– несмещённые (значение математического ожидания оценки совпадает со значением оценивающего параметра, то есть );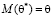

– смещённые (оценка );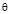

– эффективные (оценка, которая имеет при заданном объёме выборки n наименьшую дисперсию);

– состоятельные (оценка, которая стремится при 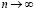по вероятности к оцениваемому параметру);

Точечной оценкой называют некоторую функцию результатов наблюдения 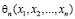, значение которой принимается за более приближенное в данных условиях к значению самого параметра θ, то есть оценку, определяющую одним числом [5, 2].

Часто, по результатам наблюдений количественного признака X требуется оценить следующие параметры распределения генеральной совокупности:

– генеральная средняя M(X);

– генеральная дисперсия D(X);

В качестве точечных оценок этих параметров выступают выборочная средняя и выборочная дисперсия 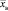и Dв соответственно [1, 4].

Генеральная средняя – среднее арифметическое значений генеральной совокупности :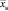

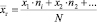
– с повторениями

Выборочная средняя – среднее арифметическое значение выборки [3, 8].

То есть, имеется выборка объёма n, тогда выборочная средняя равна:

.

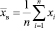
Выборочная средняя по данным одной выборки является определённым числом. Также выборочная средняя является несмещённой оценкой математического ожидания.

При увеличении объёма выборки n вся выборочная система стремится к генеральной средней [6, 9].

Генеральной дисперсией называют среднеарифметическое квадратное отклонение значений генеральной совокупности от их среднего значения.

Кроме дисперсий для характеристики рассеивания значений генеральной совокупности вокруг своего среднего также можно пользоваться средним квадратическим отклонением [10].

Выборочная дисперсия – среднее арифметическое квадратов отклонений, наблюдаемых значений выборки от их среднего значения.

Справедлива также формула:

.

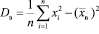
Для исправления выборочной дисперсии необходимо умножить её на дробь:

.

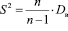
Получаем исправленную выборочную дисперсию, которая является несмещённой оценкой генеральной дисперсии.

– с повторениями.

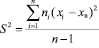
Для оценки рассеивания выборки служит выборочное среднеквадратическое отклонение.

Теперь рассмотрим, как применяются перечисленные данные при решении задач.

Из генеральной совокупности извлечена выборка объёма n=30;

Источник