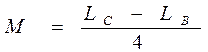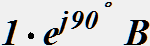цепь со взаимной индуктивностью м 5 мгн имеет параметры l1 l2 15 мгн
ЦЕПИ СО ВЗАИМНОЙ ИНДУКТИВНОСТЬЮ
3.1 Цель работы:исследование характеристик цепей с взаимной индуктивностью.
3.2 Оборудование и материалы: электрический стенд для исследования цепей со взаимной индуктивностью, генератор «Электроника», милливольтметр В3-33.
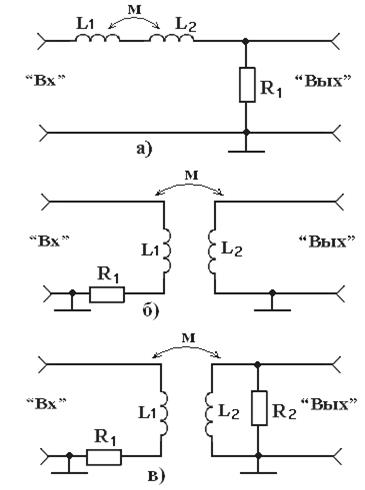
Принципиальная электрическая схема стенда представлена на рисунке 3.1. С помощью гнезда 1,…12 и соединительных проводов между гнездами 1, 2 (вход) и 3, 4 или 9, 10 (выход) стенда обеспечиваются включение одной из исследуемых цепей. Упрощенные принципиальные схемы стенда приведены на рисунках 3.2 – 3.3 Схемы рисунков 3.2 и 3.3а образуются путем подключения выводов индуктивностей L1 и L2 или последовательно соединенных индуктивностей L1 и L2 к гнездам 5, 6. Для получения схемы рисунка 3.3б индуктивность L1 подключается к гнездам 5, 6, индуктивность L2 – к гнездам 7, 8. Для получения схемы рисунка 3.3в необходимо соединить между собой гнезда 11, 12.
Рисунок 3.1 – Принципиальная схема стенда

Рисунок 3.3 – Упрощенные принципиальные схемы стенда
При выполнении лабораторного задания возникает необходимость в измерении тока через индуктивность. В настоящей работе такое измерение выполняется косвенно. Последовательно с индуктивностью включается один из резисторов R1 или R2, сопротивление каждого из которых (300 Ом) значительно меньше индуктивного сопротивления катушки и практически не влияет на величину тока в цепи. О величине тока судят по напряжению на сопротивлении. Гнезда 1, 2 (вход) предназначены для подключения низкочастотного генератора. Напряжение на входе стенда устанавливается и контролируется по измерительному прибору генератора или с помощью милливольтметра, подсоединенного к гнездам 1, 3. Гнезда «Вых» предназначены для подключения милливольтметра к выходу исследуемой цепи. В качестве гнезд «Bыx» используются гнезда 3, 4 или 9, 10.
Сведения из теории
Две электрические цепи называются индуктивно связанными, если в них находятся э.д.с. взаимной индукции. Индуктивная связь между такими цепями характеризуется взаимной индуктивностью М, равной отношению потокосцепления взаимной индукции в одной цепи к току в другой:
 |  |
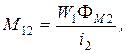

где 
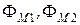


Для линейных электрических цепей 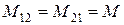

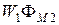
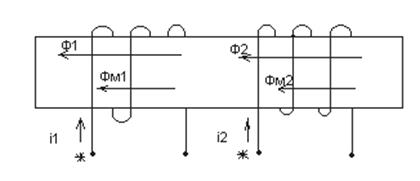
Положительные направления токов i1 и i2 в двух индуктивно связанных катушках считают согласными, если положительные направления создаваемых ими магнитных потоков самоиндукции Ф1, Ф2 и взаимной индукции 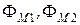
Рисунок 3.4 – Согласное направление токов в индуктивно связанных
Катушках
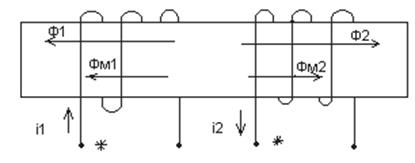
Рисунок 3.5 – Встречное направление токов в индуктивно связанных катушках
При согласном направлении токов i1 и i2 в двух индуктивно связанных катушках выводы этих катушек, относительно которых токи направлены одинаково, называются одноименными или однополярными. На рисунках 3.4, 3.5 эти выводы обозначены точками. Одноименные выводы индуктивно связанных катушек характеризуются тем, что при одинаковом направлении токов i1 и i2 относительно этих выводов магнитные потоки самоиндукции и взаимной индукции в каждой катушке складываются. Поэтому при изображении электрических принципиальных схем электрических устройств намотка витков индуктивно связанных катушек не показывается, а обозначаются их одноименные выводы.
При последовательном согласном включении двух индуктивно связанных катушек (рисунок 3,6а) суммарное мгновенное значение напряжения uc будет равно:
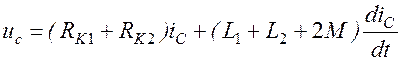
где 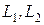
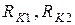

Последовательное включение катушек индуктивности.
Рисунок 3.6 – Способы включения катушек индуктивности:
а) согласное включение; б) встречное включение
Индуктивность цепи 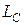
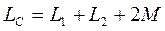
При последовательном встречном включении двух индуктивно связанных катушек (рисунок 3.6 б) суммарное мгновенное значение напряжения будет равно:
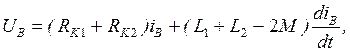
где 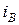
Индуктивность цепи 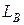

Если в цепи с индуктивно связанными катушками действует гармоническая э.д.с., то расчет такой цепи проводят методом комплексных амплитуд. Выражения (3.3), (3.5) будут иметь тогда следующий вид:
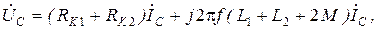

Из выражений (3.7), (3.8) можно легко найти токи 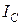


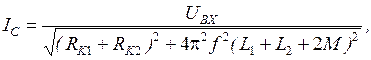
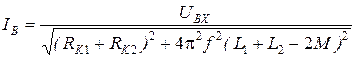
Если 
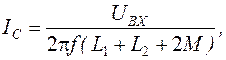

Величина 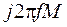
Для количественной характеристики двух индуктивно связанных катушек используется коэффициент связи k определяемый выражением:

Две индуктивно связанные и включенные параллельно катушки индуктивности без сердечника образуют воздушный трансформатор (рисунок 3.7). Если токи и напряжения на входе и выходе трансформатора обозначить через 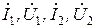
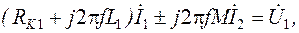

Рисунок 3.7 – Электрическая схема воздушного трансформатора
Определяя из выражения (3.15) ток 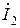
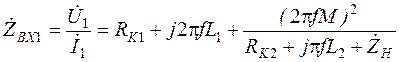
Третье слагаемое в выражении (3.15) представляет собой комплексное сопротивление 
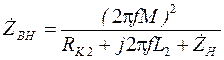
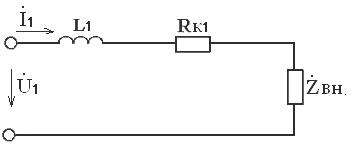
Схема замещения трансформатора представлена на рисунке 3.8. Если сопротивление нагрузки активно 
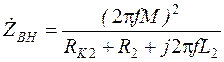
Рисунок 3.8 – Схема замещения воздушного трансформатора
Активная 
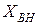
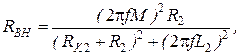
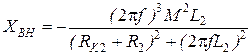
В режиме холостого хода 
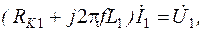

Ток в первичной обмотке трансформатора 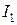
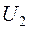
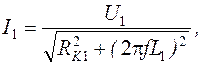
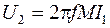
Величина n, определяемая как отношение напряжений 

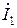
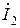
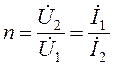
Подготовка к лабораторной работе
3.4.1 Рассчитать индуктивность двух одинаковых катушек L1 и L2 и взаимную индуктивность М между ними по заданным индуктивностям при согласного 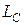
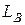
3.4.2 Рассчитать действующее значение тока в цепи (рисунок 3.3а) при согласном и встречном включении катушек L1 и L2. Индуктивности 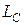
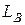
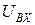

3.4.3 Для воздушного трансформатора, изображенного на рисунке 3.3б, в, рассчитать, используя результаты п. 3.4.1, напряжение на вторичной обмотке и ток через первичную обмотку при отключенной нагрузке R2, то есть в режиме холостого хода. Величинами 
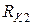


3.4.4 Используя результаты п. 3.4.1, рассчитать активную 

Величины R2=300 Ом, 

Порядок выполнения работы
3.5.1 Установить на входе стенда гармонический сигнал частотой 

3.5.2 С целью вычисления индуктивности L1 определить ток через нее, для чего собрать схему, представленную на рисунке 3.2а, и измерить напряжение на резисторе R1.
3.5.3 Для вычисления индуктивности катушки L2 собрать схему, изображенную на рисунке 3.2б, и измерить напряжение на резисторе R1.
3.5.4 Для вычисления индуктивности согласно включенных катушек L1 и L2 собрать схему, представленную на рисунке 3.3а, катушки включить согласно и измерить напряжение на резисторе R1.
3.5.5 Для определения индуктивности встречно включенных катушек L1 и L2 собрать схему, изображенную на рисунке 3.2а, катушки включить встречно и измерить напряжение на резисторе R1.
3.5.6 Собрать схему, представленную на рисунке 3.3б, и измерить напряжение на вторичной обмотке трансформатора при холостом ходе и напряжение на резисторе R1.
3.5.7 Собрать схему, изображенную на рисунке 3.3в, и измерить напряжение на вторичной обмотке нагруженного трансформатора и на резисторе R1 (для определения тока первичной обмотки нагруженного трансформатора).
Обработка результатов
3.6.1 По результатам п. 3.5.2 определить индуктивность катушки L1 при R1=300 Ом. Расчет произвести по формуле:
где 

3.6.2 По результатам п. 3.5.3 определить индуктивность катушки L2, используя для этого приведенное выше выражение (R1=300 Ом).
3.6.3 По результатам п. 3.5.4 определить индуктивность согласно включенных катушек L1 и L2.
3.6.4 По результатам п. 3.5.3 определить индуктивность встречено включенных катушек L1 и L2.
3.6.5 Используя результаты пп. 3.6.3, 3.6.4, найти взаимную индуктивность М между катушками по формуле:
3.6.6 По результатам п. 3.5.6 определять ток первичной обмотки трансформатора при холостом ходе. R1=300 Ом.
3.6.7 По результатам п. 3.5.7 определить ток первичной обмотки нагруженного трансформатора.
3.6.8 Определить абсолютные и относительные погрешности измерений.
Контрольные вопросы
1. Какие цепи называют связанными?
2. Какие виды связи возможны между цепями?
3. Что такое коэффициент связи двух контуров?
4. Чему равен коэффициент связи двух контуров, связанных магнитно?
5. Какое включение двух магнитно связанных цепей называют согласным и какое встречным?
6. Как экспериментально определить взаимную индуктивность между двумя катушками?
7. Что называется воздушным трансформатором?
8. Чему равно напряжение на зажимах разомкнутой вторичной цепи воздушного трансформатора?
9. Что такое вносимое сопротивление?
10. Где целесообразно применять воздушные трансформаторы?
11. Что такое коэффициент трансформации?
12. Нарисовать схему замещения воздушного трансформатора.
13. Построить векторную диаграмму напряжений и токов для воздушного трансформатора.
Рекомендуемая литература
[1, c.129–146; 2, c. 103–121; 3, c. 200–213, 4, c. 242–252].
Основы теории цепей-2
для специальностей 200700, 200701, 200702, 200703
Теория электрических цепей-2
для специальностей 071700, 075300, 201100, 201400, 201500
Кафедра ТОР
Тельпуховская Л.И., Каминский В.Л.
Томск-2002
№ 1
Схема цепи, для которой справедлива представленная зависимость входного сопротивления от частоты.
•
№ 2
АЧХ коэффициента передачи по напряжению в цепи со следующей схемой.
•
№ 3
С какого элемента цепи представленной схемы следует снимать выходное напряжение, чтобы получить АЧХ коэффициента передачи по напряжению следующего вида:
№ 4
Схема цепи, для которой справедлива представленная частотная зависимость входного сопротивления.
•
№ 5
Значения входного сопротивления цепи на постоянном токе Z(0) и на бесконечно большой частоте Z(∞).
• Z(0) = 50 Ом, Z(∞) = 40 Ом.
№ 6
Два варианта схемы цепи, для которых АЧХ коэффициента передачи по напряжению представлена следующей зависимостью:
•
№ 7
АЧХ коэффициента передачи по напряжению в цепи со следующей схемой:
•
№ 8
Каковы значения входного сопротивления представленной цепи на постоянном токе Z(0) и на бесконечно большой частоте Z(∞).
• Z(0) = 5 кОм, Z(∞) = 5 кОм.
№ 9
С какого элемента цепи представленной схемы необходимо снимать выходное напряжение, чтобы получить АЧХ коэффициента передачи по напряжению следующего вида:
№ 10
Вычислите значения входного сопротивления представленной цепи на постоянном токе Z(0) и на бесконечно большой частоте Z(∞).
№ 1
Как изменится амплитуда напряжения на выходе цепи при частоте f=0,6 МГц, если параллельно к резистору R подключить сопротивление, равное 4000 Ом, причем R = 10 3 Ом, С=100пФ.
№ 3
Выражение АЧХ коэффициента передачи цепи по напряжению и определить граничную частоту полосы пропускания.
• 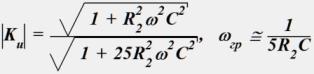
№ 4
Коэффициент передачи по напряжению на частоте ω = 1/5 рад/c, если C1 = 1 Ф, C2 = 1 Ф, R1 = R2 = 5 Ом.
№ 5
Для цепи, имеющей представленную ниже схему, определить частоту ω, на которой выходной сигнал в 4 раза меньше входного.
• 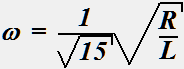
№ 6
Выражение для ωгр цепи, схема которой представлена ниже:
• 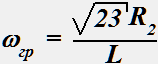
№ 7
Определите входное сопротивление цепи, если на некоторой частоте сопротивления участков цепи заданы в омах:
• 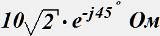
№ 8
Записать выражение для коэффициента передачи по напряжению цепи, схема которой представлена на рисунке ниже, причем: L = 5 Гн, R1 = 2 Ом, R2 = 2 Ом, ω = 5 рад/c.
№ 9
Определить сопротивление цепи, если на некоторой частоте сопротивление каждого элемента указано в омах. Представьте эквивалентную схему замещения на этой частоте.
•
№ 10
На вход последовательной RL цепи подано гармоническое колебание i(t) = cos 10 6 t, мА. Напряжение на индуктивности, если L = 1 мГн.
•
№ 2
Рассчитайте добротность последовательного контура, у которого сопротивление потерь R = 5 Ом, и на некоторой частоте f |XC|= 225 Ом, |XL|= 144 Ом.
• 36.
№ 3
Укажите величину напряжения на сопротивлении R при резонансе, если добротность контура Q = 50.
№ 4
Рассчитайте L и R контура, настроенного последовательно, если амплитуда напряжения на емкости должна быть 10 В, полоса пропускания 15 кГц, емкость контура С = 100 пФ, э.д.с., действующая на контур, имеет амплитуду Em = 0,1 В.
• 11 мГн, 10 Ом.
№ 5
Рассчитайте полосу пропускания последовательного контура, у которого R = 50 Ом, L = 500 мГн.
• 100 рад/c;
• 16 Гц.
№ 6
Какое шунтирующее сопротивление необходимо подключить к емкости последовательного колебательного контура, чтобы увеличить его полосу пропускания в два раза, если контур имел сопротивление потерь R = 10 Ом, характеристическое сопротивление ρ = 200 Ом.
• 2 кОм.
№ 7
Найдите абсолютную Δf, относительную и обобщенную расстройки контура, при которых ток уменьшится до 0,4 своего резонансного значения, если Q = 100, fρ = 5*10 6 Гц.
• ζ = 3,89, Δf = 97 кГц, Δf / fro = 0,0195.
№ 8
Определите амплитуду напряжения на емкости при расстройке Δf = 36 кГц, если к последовательному контуру подключен источник напряжения с амплитудой E = 2 В и частотой 3 Мгц. Контур настроен на частоту источника и имеет следующие параметры: R = 400 Ом, C = 60 пФ.
• 39 В.
№ 9
Определите амплитуду напряжения на емкостном элементе на частоте ω, которая больше резонансной частоты на 0,5%. Добротность контура Q = 40, подводимое к контуру напряжение U = 0,4 cos ω t, В.
• 13 В.
№ 10
Рассчитайте параметры L,C,R,Q последовательного контура, на который действуют одновременно сигнал ec(t) = 2*cos 2*10 5 t мВ и помеха en(t) = 20*cos 10 6 t мВ.
Составляющая напряжения на конденсаторе, созданная сигналом, превосходит составляющую, созданную помехой в 8 раз, и составляющая тока с частотой сигнала равна 0,5 мА.
• L=236 мкГн, С=4210пФ, R= 40 Ом, Q=7,9.
№ 1
Определение характеристического сопротивления контура:
• Сопротивление индуктивности или емкости контура на резонансной частоте.
№ 2
Резонансная частота последовательного колебательного контура определяется:
• Величинами емкости и индуктивности контура.
№ 3
Неверное выражение добротности контура:
• Q = 2Δ ωп / ωp.
№ 4
В основе определения резонанса напряжений в последовательном колебательном контуре лежит соотношение:
• Uср = QEвх.
№ 5
Как изменится резонансная частота последовательного контура при подключении к его конденсатору измерительного прибора, имеющего входную емкость C0?
• Уменьшится.
№ 6
Относительная полоса пропускания определяется:
• 2Δω / ωp;
• R / Lωp.
№ 7
Добротность последовательного колебательного контура при подключении к его конденсатору шунтирующего сопротивления Rш:
• Уменьшится.
№ 8
Каковы амплитуды напряжения на реактивных элементах последовательного колебательного контура при резонансе, если на входе действует сигнал e(t) = Emcos ωt:
• Uср = ULp = QEm.
№ 9
Амплитуда тока на резонансной частоте в последовательном колебательном контуре:
• Ip = E/R.
№ 10
Определение абсолютной настройки контура Δω (или Δf):
• Разность между частотой источника сигнала и резонансной частотой контура.
№ 1
Входное сопротивление двухполюсника, если сопротивление отдельных участков цепи указаны в омах:
№ 2
Резонансное сопротивление параллельного контура, у которого L = 100 мкГн, C = 100 пФ, R = 10 Ом.
• 10 5 Ом.
№ 3
Как следует распределить индуктивность контура между ветвями, чтобы его сопротивление было равно 10 кОм. Контур имеет R=10 Ом, C=600 пФ, L∑ = 150 мкГн.
• L1 = 94,5 мкГн, L2 = 55,5 мкГн.
№ 4
Мощность, выделяемая в простом параллельном контуре, если резонансное сопротивление Rρ = 40 кОм, амплитуда тока в контуре 0,6 А, добротность Q=30.
• 8 Вт.
№ 5
Мощность на контуре в момент резонанса токов, если резонанс напряжений наступает на частоте 10 6 рад/с. Параметры контура следующие: R1 = R2 = 5 Ом, C = 1000 пФ, L1 = 500 мкГн, E = 10 В.
№ 6
Схема параллельного контура, для которого резонанс напряжений наступает на частоте ωp = 1/√(L2C1).
•
№ 7
Для контура 2-го вида выражение индуктивного коэффициента включения Р, если L0 = L1 + L2.
№ 8
Выбрать внутреннее сопротивление генератора Ri, чтобы избирательные свойства контура при подключении генератора к контуру не ухудшились.
№ 9
Зависимость Zвх(ω) параллельного контура с разделенными индуктивностями.
•
№ 10
Чему равно сопротивление контура с разделенными конденсаторами на частоте параллельного резонанса, если Q=50, коэффициент включения р=0,5, сопротивление потерь контура R=10 Ом.
• Rрсл = 6,25 кОм.
№ 1
Как изменится входное сопротивление системы связанных колебательных контуров при размыкании ключа, если ωp1 = ωp2 = ωген, а связь оптимальная?
• Уменьшится в два раза.
№ 2
Система из двух колебательных контуров при связи выше критической имеет:
• Три резонансных частоты.
№ 3
Как изменится входное сопротивление системы связанных контуров при замыкании ключа, при условии: ωp1 = ωp2 = ωген, связь оптимальная?
• Уменьшится в два раза.
№ 4
Входное сопротивление системы связанных контуров, если на некоторой частоте сопротивления участков цепей системы указаны в омах.
№ 5
Тип резонанса в системе связанных колебательных контуров. Известно, что частота генератора равна 2*10 6 рад/с, L1 = 250 мкГн, С1 = 250 пФ. В системе имеет место оптимальный резонанс.
• Сложный.
№ 6
Эквивалентное (входное) сопротивление связанной системы, последовательно подключенной к генератору, на частоте f=159 кГц. Параметры двух связанных индуктивной связью контуров следующие: L1 = 510 мкГн, L2 = 208 мкГн, C1 = 2000 пФ, C2 = 5000 пФ, R1 = 2 Ом, R2 = 6 Ом, M = 7 мкГн.
• Żэ = 4,94 + j6,08 Ом.
№ 7
Частоты связи системы их двух одинаковых контуров, настроенных каждый в отдельности на частоту f0 = 2*10 6 Гц. Известно, что активное сопротивление каждого контура R=10 Ом, а сопротивление связи Xсв = 16 Ом. Емкость каждого контура равна 100 пФ.
• f2 = 2015,7 кГц, f3 = 1984,3 кГц;
• f2 = 16858,7 рад/с, f3 = 12363,4 рад/с.
№ 8
Рассчитать емкость C1 первого контура так, чтобы было выполнено условие частного резонанса. Колебательные контуры имеют следующие параметры: L1 = 200 мкГн, L2 = 250 мкГн, R2 = 100 Ом, C2 = 900 пФ, M = 40 мкГн, f = 700 кГц.
• 270 пФ.
№ 9
Мощность, расходуемая в первом и во втором контурах, если даны два индуктивно-связанных контура со следующими параметрами: L1 = 400 мкГн, С1 = 310 пФ, R1 = 16 Ом,
L2 = 410 мкГн, С2 = 290 пФ, R2 = 14 Ом, f = 460*10 3 Гц, U1 = 100 В, M = 36 мкГн.
• P1 = 0,205 Вт, P2 = 5,68 Вт.
№ 10
Мощность, отдаваемая во второй контур, и вид резонанса в системе двух связанных контуров со следующими параметрами: L1 = L2 = 0,5 мГн, R1 = R2 = 10 Ом, ωp1 = ωp2 = 10 6 рад/c, M = 20 мкГн, e(t) = 4cos10 6 t, В.
• P2 = 128 мВт, резонанс индивидуальный.
№ 1
А-параметры четырехполюсника (ЧП) определяются при режимах работы:
• Х.Х. (холостой ход) на выходе и К.З. (короткое замыкание) на выходе.
№ 2
Система уравнений, для которой матрица параметров [МП] выражается через Y-параметры:
• 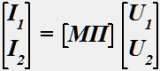
№ 3
При каскадном соединении двух четырехполюсников (ЧП) результирующая матрица параметров равна выражению:
• [A] = [A1]*[A2].
№ 4
Y-параметры четырехполюсника (ЧП) определяются при:
• Х.Х. на выходе и Х.Х. на входе.
№ 5
Условием максимальной передачи мощности от четырехполюсника в нагрузку является утверждение:
• Равенство комплексно-сопряженных сопротивлений выхода ЧП и нагрузки Żвыхчп = Ż*н.
№ 6
Физический смысл и размерность параметра A11.
• Безразмерная величина, обратная коэффициенту передачи ЧП при холостом ходе на выходе.
№ 7
Характеристическими называются параметры ЧП:
• Постоянная распространения, характеристические сопротивления.
№ 8
Результирующая матрица эквивалентных параметров для параллельного соединения двух четырехполюсников:
№ 9
Для согласованного ЧП затухание 40 дБ соответствует уменьшению напряжения или тока в:
• 100 раз.
№ 10
Для согласованного ЧП 1 Неп соответствует изменению напряжения или тока в:
• 2,72 раза.
№ 11
Модуль определителя матрицы Y-параметров для четырехполюсника.
№ 15
Характеристические сопротивления ZC1 и ZC2 для схемы четырехполюсника, у которого параметры на некоторой частоте указаны в омах.
№ 16
Для Т-образного симметричного четырехполюсника вычислить характеристические сопротивления. Значения элементов указаны в омах.
№ 17
Характеристическое затухание ac и фазовая постоянная bc на основе соотношения gc = ln(√(A11A22) + √(A12A21)). Параметры указаны на схеме в омах.
№ 18
Y-параметры ЧП, для которого сопротивления на схеме указаны в омах.
№ 20
Характеристическое затухание ac и характеристическая фазовая постоянная bc полузвена меньше соответствующих величин ac, bc полного звена:
• В два раза.
№ 1
Если на некоторой частоте ω оба двухполюсника состоят из единственного реактивного элемента, то тип фильтра представленный на схеме:
№ 2
Для схемы фильтра, определить частоту среза.
№ 3
Параметры ФНЧ L и С, имеющего ωср = 4000 рад/с и характеристическое сопротивление R0 = 50 Ом.
• С=10 мкФ, L=25 мГн.
№ 4
Параметры L и С ФВЧ, обеспечивающего частоту среза ωср = 2000 рад/с и имеющего номинальное характеристическое сопротивление R0 = 75 Ом.
• С=3,33 мкФ, L=37,5 мГн.
№ 5
Характеристическое сопротивление для Т-образной схемы ФНЧ на частоте ω = 1/2 ωср при условии, что номинальное характеристическое сопротивление R0 = 75 Ом.
• 64,95 Ом.
№ 6
Характеристическое сопротивление для П-образной схемы ФВЧ на частоте ω = 1/2 ωср, при номинальном характеристическом сопротивлении R0 = 75 Ом.
• |ZСП| = 43 Ом, характер емкостный.
№ 7
Для m=0,6 индуктивность поперечной ветви последовательно-производного фильтра нижних частот типа ‘m’, при частоте среза ФНЧ типа ‘к’ равна ωср = 4000 рад/с, а номинальное характеристическое сопротивление R0 = 50 Ом.
• L=13,4 мГн.
№ 8
Для m=0,5 индуктивность поперечной ветви последовательно-производного фильтра верхних частот типа ‘m’, при частоте среза ωср = 2000 рад/с, а номинальное характеристическое сопротивление R0 = 75 Ом.
• L=18,75 мГн.
№ 9
Для согласованного фильтра затухание в 40 дБ соответствует уменьшению амплитуды напряжения или тока в:
• 100 раз.
№ 10
Затухание ФНЧ на частоте ω = 2ωср. Выразить затухание в неперах, децибелах и простых числах.
• 2,64 нп, 23 дБ, 7.
№ 11
Какому типу фильтра соответствует частотная зависимость затухания?
•
№ 12,13
Схема фильтра, для которого представлена зависимость характеристического сопротивления Zc от частоты ω.
•
•
№ 15
Какому типу фильтра соответствует представленная фазовая характеристика?
№ 16
Выражение, соответствующее частоте среза (ωср) для схемы:
№ 18
Последовательно-производное звено ФНЧ типа ‘m’:
•
№ 19
Параллельно-производное звено ФВЧ типа ‘m’:
•
№ 20
Нагрузка фильтра, когда его входное сопротивление равняется характеристическому:
• Zн = ρ.
№ 2
Входное сопротивление линии на частоте f = 3*10 6 Гц, если длина линии равна l=5 м, волновое сопротивление ρ = 100 Ом, и линия нагружена на индуктивное сопротивление, равное 50 Ом.
• 198,2 Ом.
№ 3
Длина воздушной короткозамкнутой линии без потерь, имеющей Żвх = j50 Ом, волновое сопротивление ρ = 150 Ом. Частота генератора, питающего линию, 75 МГц.
• 0,2 м.
№ 4
Затухание линии ac, если волновое сопротивление длинной линии ρ = 100 Ом, а погонное сопротивление линии составляет 230 Ом/км. Примечание: погонной проводимостью пренебречь, ac ≅ (R/2ρ) + (1/2Gρ).
• 1,15 нп/км.
№ 5
Скорость распространения радиоволн в линии без потерь и длину волны, если линия имеет погонные параметры С=16пФ/м, L=1мкГн/м, частота питающего генератора f=25МГц.
• 2,5*10 8 м/с, 10 м.
№ 7
Волновое сопротивлене разомкнутой линии, для которой были проведены два измерения: напряжение в конце линии Uк = 400 В, и ток на расстоянии, равном 2 м от конца линии, I=1 А. Длина волны генератора λ = 20 м.
• 235 Ом.
№ 8
Коэффициент отражения в длинной линии, для которой распределение амплитуды напряжения представлено следующим графиком:
№ 9
Коэффициент стоячей волны в длинной линии, если коэффициент бегущей волны равен 0,25.
• 4.
№ 10
Рассчитать нагрузочное сопротивление воздушной длинной линии без потерь так, чтобы входное сопротивление было равно 0. Длина линии l=30 м, ρ = 100 Ом, генератор, питающий линию, работает на частоте f = 2*10 6 Гц.
• 308 Ом.
№ 1
Режим работы длинной линии без потерь, для которой распределение сопротивления по ее длине представлено следующим графиком:
• Режим стоячих волн при холостом ходе на выходе.
№ 2
Коэффициент бегущей волны определяется:
• Umin/Umax.
№ 3
Разомкнутую длинную линию без потерь в точке l = λ/4 можно заменить эквивалентной схемой:
• Настроенным последовательным контуром без потерь.
№ 4
Вид нагрузки длинной линии без потерь, для которой распределение амплитуды тока и напряжения вдоль ее линии представлено на следующем графике:
№ 5
Эквивалентная схема замещения разомкнутого отрезка линии без потерь длиной l = λ.
•
№ 6
В линии без потерь устанавливается режим бегущей волны при нагрузке:
• Żн = ρ.
№ 8
Выражение для коэффициента фазы длинной линии.
• β = 2π/λ;
• β = ω√(LC);
• β = ωT/λ.
№ 9
Волновое сопротивление линии без потерь (ρ) определяется выражением:
• ρ = √(L/C);
• ρ = Uпад/Iпад;
• ρ = Uотр/Iотр.
№ 10
Распределение амплитуд напряжения и тока в линии без потерь, нагруженной на активное сопротивление Rн Другие статьи по теме