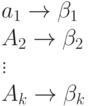вычислить среднюю длину кода
Код Хаффмана
Построение кода Хаффмана для таблицы вероятностей.
Вот калькулятор, который рассчитывает коды Хаффмана для заданной вероятности символов.
Немного теории под калькулятором.
Код Хаффмана
Таблица вероятности символов
Таблица вероятности символов
Импортировать данные Ошибка импорта
Небольшой отрывок из Википедии.
Алгоритм Хаффмана — адаптивный жадный алгоритм оптимального префиксного кодирования алфавита с минимальной избыточностью. Был разработан в 1952 году аспирантом Массачусетского технологического института Дэвидом Хаффманом при написании им курсовой работы. В настоящее время используется во многих программах сжатия данных.
Этот метод кодирования состоит из двух основных этапов:
Построение оптимального кодового дерева.
Построение отображения код-символ на основе построенного дерева.
Идея алгоритма состоит в следующем: зная вероятности символов в сообщении, можно описать процедуру построения кодов переменной длины, состоящих из целого количества битов. Символам с большей вероятностью ставятся в соответствие более короткие коды. Коды Хаффмана обладают свойством префиксности (т. е. ни одно кодовое слово не является префиксом другого), что позволяет однозначно их декодировать.
Классический алгоритм Хаффмана на входе получает таблицу частот встречаемости символов в сообщении. Далее на основании этой таблицы строится дерево кодирования Хаффмана (Н-дерево).
Этот процесс можно представить как построение дерева, корень которого — символ с суммой вероятностей объединенных символов, получившийся при объединении символов из последнего шага, его n0 потомков — символы из предыдущего шага и т. д.
Чтобы определить код для каждого из символов, входящих в сообщение, мы должны пройти путь от корня до листа дерева, соответствующего текущему символу, накапливая биты при перемещении по ветвям дерева (первая ветвь в пути соответствует младшему биту). Полученная таким образом последовательность битов является кодом данного символа, записанным в обратном порядке.
Вычислить среднюю длину кода
Коды Фано и Хаффмана являются оптимальными и префиксными. При построении искомых кодов будем применять как традиционный табличный способ кодирования, так и использовать «кодовые деревья».
При кодировании по Фано все сообщения записываются в таблицу по степени убывания вероятности и разбиваются на две группы примерно (насколько это возможно) равной вероятности. Соответственно этой процедуре из корня кодового дерева исходят два ребра, которым в качестве весов присваиваются полученные вероятности. Двум образовавшимся вершинам приписывают кодовые символы 0 и 1. Затем каждая из групп вероятностей вновь делится на две подгруппы примерно равной вероятности. В соответствии с этим из каждой вершины 0 и 1 исходят по два ребра с весами, равными вероятностям подгрупп, а вновь образованным вершинам приписывают символы 00 и 01, 10 и 11. В результате многократного повторения процедуры разделения вероятностей и образования вершин приходим к ситуации, когда в качестве веса, приписанного ребру бинарного дерева, выступает вероятность одного из данных сообщений. В этом случае вновь образованная вершина оказывается листом дерева, т.к. процесс деления вероятностей для нее завершен. Задача кодирования считается решенной, когда на всех ветвях кодового бинарного дерева образуются листья.
Пример 151. Закодировать по Фано сообщения, имеющие следующие вероятности:
| сообщение | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| вероятность | 0,4 | 0,2 | 0,1 | 0,1 | 0,1 | 0,05 | 0,05 |
Решение 1 (с использованием кодового дерева)
Листья кодового дерева представляют собой кодируемые сообщения с присвоенными им кодовыми словами.
Решение 2 (табличный способ)
Цена кодирования (средняя длина кодового слова является критерием степени оптимальности кодирования. Вычислим ее в нашем случае.
Для того, чтобы закодировать сообщения по Хаффману, предварительно преобразуется таблица, задающая вероятности сообщений. Исходные данные записываются в столбец, две последние (наименьшие) вероятности в котором складываются, а полученная сумма становится новым элементом таблицы, занимающим соответствующее место в списке убывающих по величине вероятностей. Эта процедура продолжается до тех пор, пока в столбце не останутся всего два элемента.
Пример 152. Закодировать сообщения из предыдущего примера по методу Хаффмана.
Решение 1. Первый шаг
Вторым шагом производим кодирование, «проходя» по таблице справа налево (обычно это проделывается в одной таблице):
Решение 2. Построение кодового дерева начинается с корня. Двум исходящим из него ребрам приписывается в качестве весов вероятности 0,6 и 0,4, стоящие в последнем столбце. Образовавшимся при этом вершинам дерева приписываются кодовые символы 0 и 1. Далее «идем» по таблице справа налево. Поскольку вероятность 0,6 является результатом сложения двух вероятностей 0,4 и 0,2, из вершины 0 исходят два ребра с весами 0,4 и 0,2 соответственно, что приводит к образованию двух новых вершин с кодовыми символами 00 и 01. Процедура продолжается до тех пор, пока в таблице остаются вероятности, получившиеся в результате суммирования. Построение кодового дерева заканчивается образованием семи листьев, соответствующих данным сообщениям с присвоенными им кодами. Дерево, полученное в результате кодирования по Хаффману, имеет следующий вид:
Листья кодового дерева представляют собой кодируемые сообщения с присвоенными им кодовыми словами. Таблица кодов имеет вид:
| сообщение | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| код | 1 | 01 | 0010 | 0011 | 0000 | 00010 | 00011 |
Цена кодирования здесь будет равна
Для передачи данных сообщений можно перейти от побуквенного (поцифрового) кодирования к кодированию «блоков», состоящих из фиксированного числа последовательных «букв».
Пример 154. Провести кодирование по Хаффману трехбуквенных комбинаций для алфавита из предыдущего примера.
Построим кодовое дерево.
Найдем цену кодирования
Решение. Составим таблицу тройного «сжатия» по методу Хаффмана
Тогда тринарное дерево выглядит следующим образом:
Вопросы для самоконтроля
1. Как определяется среднее число элементарных сигналов, приходящихся на одну букву алфавита?
3. Сколько требуется двоичных знаков для записи кодированного сообщения?
4. На чем основано построение кода Фано?
5. Что такое сжатие алфавита?
6. Какой код самый выгодный?
7. Основная теорема о кодировании.
8. Энтропия конкретных типов сообщений.
I 301. Проведите кодирование по методу Фано алфавита из четырех букв, вероятности которых равны 0,4; 0,3; 0,2 и 0,1.
302. Алфавит содержит 7 букв, которые встречаются с вероятностями 0,4; 0,2; 0,1; 0,1; 0,1; 0,05; 0,05. Осуществите кодирование по методу Фано.
304. Проведите кодирование по методу Хаффмана трехбуквенных слов из предыдущей задачи.
305. Проведите кодирование 7 букв из задачи 302 по методу Хаффмана.
306. Проведите кодирование по методам Фано и Хаффмана пяти букв, равновероятно встречающихся.
II 307. Осуществите кодирование двухбуквенных комбинаций четырех букв из задачи 301.
308. Проведите кодирование всевозможных четырехбуквенных слов из задачи 303.
III 309. Сравните эффективность кодов Фано и Хаффмана при кодировании алфавита из десяти букв, которые встречаются с вероятностями 0,3; 0,2; 0,1; 0,1; 0,1; 0,05; 0,05; 0,04; 0,03; 0,03.
310. Сравните эффективность двоичного кода Фано и кода Хаффмана при кодировании алфавита из 16 букв, которые встречаются с вероятностями 0,25; 0,2; 0,1; 0,1; 0,05; 0,04; 0,04; 0,04; 0,03; 0,03; 0,03; 0,03; 0,02; 0,02; 0,01; 0,01.
Рассчитать среднюю длину кода при методе Хаффмана
Помощь в написании контрольных, курсовых и дипломных работ здесь.

Здравствуйте. Мне нужна программа, в которой используются двухмерные массивы. Массив должен.
Определить среднюю длину слова в введенной текстовой строке, символы пунктуации на длину не влияют
определить среднюю длину слова в введенной текстовой строке, символы пунктуации на длину не влияют.

Написать функцию, находящую среднее значение в массиве с известным числом элементов. Написать.
Решение
Рассчитать среднюю наработку на отказ
процессор имеет интенсивность отказа (λ) = 10^(-6) 1/c, интенсивность восстановления (µ) = 10^(-4).
Как рассчитать среднюю цену в 1с
Здравствуйте! Не могли бы подсказать, как сделать чтобы рассчитывало среднюю цену. Например если в.
StringGrid: Рассчитать среднюю температуру за месяц
как будет выглядеть код к этой задаче? Рассчитать среднюю температуру за месяц. Написать функцию.
Рассчитать среднюю ёмкость для трёх конденсаторов
Написать программу решения следующей задачи, используя модуль: Ёмкость плоского конденсатора.
Информационные технологии
Неравномерное кодирование. Средняя длина кодирования
В приведенных выше примерах кодирования все кодовые слова имели одинаковую длину. Однако это не является обязательным требованием. Более того, если вероятности появления сообщений заметно отличаются друг от друга, то сообщения с большой вероятностью появления лучше кодировать короткими словами, а более длинными словами кодировать редкие сообщений. В результате кодовый текст при определенных условиях станет в среднем короче.
Наиболее экономным является код с наименьшей средней длиной 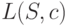
Пусть источник содержит 4 сообщения 


 | 00 |
 | 01 |
| A_3 | 10 |
| A_4 | 11 |
Очевидно, что для представления (передачи) любой последовательности в среднем потребуется 2 знака на одно сообщение. Сравним эффективность такого кодирования с описанным выше кодированием словами переменной длины. Кодовая таблица для данного случая может иметь следующий вид.
 | 0 |
 | 1 |
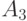 | 10 |
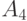 | 11 |
В этой таблице, в отличие от предыдущей, наиболее частые сообщения 

в то время как для равномерного кода средняя длина 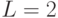
Необходимо отметить, что неоднозначность декодирования слова появилась несмотря на то, что условие однозначности декодирования знаков (инъективность кодового отображения) выполняется.
Решение данной проблемы заключается в том, чтобы иметь возможность в любом кодовом тексте выделять отдельные кодовые слова без использования специальных разделительных знаков. Иначе говоря, необходимо, чтобы код удовлетворял следующему требованию: всякая последовательность кодовых знаков может быть единственным образом разбита на кодовые слова. Коды, для которых последнее требование выполнено, называются однозначно декодируемыми (иногда их называют кодами без запятой).
Рассмотрим код (схему алфавитного кодирования) 
и различные слова, составленные из элементарных кодов.
Определение. Код 
Если таблица кодов содержит одинаковые кодовые слова, то есть если
то код заведомо не является однозначно декодируемым (схема не является разделимой). Такие коды далее не рассматриваются.
Префиксные коды
Наиболее простыми и часто используемыми кодами без специального разделителя кодовых слов являются так называемые префиксные коды [29].
Теорема 1. Префиксный код является однозначно декодируемым.
Множество кодовых слов можно графически изобразить как поддерево словарного дерева (рис.6.5). Для этого из всего словарного дерева следует показать только вершины, соответствующие кодовым словам, и пути, ведущие от этих вершин к корню дерева. Такое поддерево называют деревом кода или кодовым деревом.
Замечание. Свойство префиксности является достаточным, но не является необходимым для однозначной декодируемости.
Если код префиксный, то, читая кодовую запись подряд от начала, мы всегда сможем разобраться, где кончается одно кодовое слово и начинается следующее. Если, например, в кодовой записи встретилось кодовое обозначение 110, то разночтений быть не может, так как в силу префиксности наш код не содержит кодовых обозначений 1, 11 или, скажем, 1101. Именно так обстояло дело для рассмотренного выше кода, который очевидно является префиксным.
Кодирование Хаффмана
Оглавление
Основы
В отличие от кода Морзе, кодирование Хаффмана не требует никаких разделителей. Разделение кодовых слов не требуется, потому что кодирование без префиксов. В результате ни одно кодовое слово не является началом другого кодового слова.
Дерево, полученное в результате кодирования Хаффмана, гарантирует оптимальное кодирование без префиксов. И. Э. Не существует метода кодирования, связанного с символами, который мог бы генерировать более короткий код, если известны вероятности появления символов.
история
алгоритм
Построение кодовой книги
Средняя длина слова
Среднюю длину кодового слова можно рассчитать тремя способами.
пример
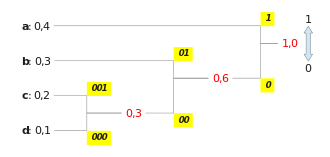
Найдите относительные частоты:
Постройте дерево Хаффмана, а затем введите кодовые слова по краям. (См. Рисунок справа)
| а | 1 |
| б | 01 |
| c | 001 |
| d | 000 |
Закодируйте исходный текст:
| Оригинал: | а | а | б | а | б | c | а | б | c | d |
| Закодировано: | 1 | 1 | 01 | 1 | 01 | 001 | 1 | 01 | 001 | 000 |
Средняя длина кодового слова:
Поскольку информационное содержание каждого символа источника не является целым числом, при кодировании остается остаточная избыточность.
Расшифровка
Для декодирования потока данных в кодировке Хаффмана необходима кодовая таблица, созданная в кодировщике (классическим методом). По сути, процедура обратная, как на этапе кодирования. Дерево Хаффмана перестраивается в декодере, и с каждым входящим битом, начиная с корня, следует соответствующий путь в дереве, пока не будет достигнут лист. Затем этот лист является исходным символом, который вы ищете, и вы снова начинаете декодировать следующий символ с корня.
пример
В декодере есть словарь кодов:
| а | 1 |
| б | 01 |
| c | 001 |
| d | 000 |
и полученное сообщение: 1101101001101001000.
Теперь путь в дереве (см. Выше) отслеживается для каждого полученного бита, начиная с корня, до тех пор, пока не будет достигнут лист. Как только лист достигнут, декодер записывает символ листа и снова начинает с корня, пока не будет достигнут следующий лист.
| Путь к детали: | 1 | 1 | 01 | 1 | 01 | 001 | 1 | 01 | 001 | 000 |
| Соответствующий лист: | а | а | б | а | б | c | а | б | c | d |
Оптимальность
Для средней длины кодового слова кода Хаффмана применяется следующее (см. Также) л ¯ <\ displaystyle <\ overline
Это означает, что в среднем каждый кодовый символ требует как минимум столько же цифр, сколько его информационное содержание, но не более одного.