что такое параметры модели в эконометрике
Параметры в эконометрике
Вы будете перенаправлены на Автор24
Параметры в эконометрических моделях
В любой задаче по эконометрике ключевым этапом является поиск параметров эконометрической модели и оценка их качества.
На практике часто используются различные параметрические модели. При этом термин «параметрический» подразумевает, что вероятностно-статистическую модель полностью описывает конечномерный вектор фиксированной размерности, которая связана с объемом выборки.
Параметрические методы анализа в эконометрике
Регрессионный анализ – это метод исследования зависимости зависимой переменной и независимых переменных. При этом в терминологии зависимых и независимых переменных отражена лишь математическая зависимости переменных, а не причинно-следственные взаимосвязи. Чтобы адекватно описать сложные внутренние неоднородные экономические процессы обычно используется система эконометрических уравнений. Для более простого случая могут быть использованы и простейшие изолированные уравнения.
Анализ временных рядов представляет собой систему математико-статистических методов исследования, которые предназначены для определения структуры временного ряда и их прогнозирования.
Необходимость выявления структуры временного ряда заключается построении математической модели явления, являющегося источником исследуемого временного ряда. К прогнозу будущих параметров временного ряда прибегают при принятии решений.
Прогнозирование опирается на некоторую заданную параметрическую модель, для чего применяются стандартные методики параметрического оценивания.
Под панельными данными понимается отслеженная во времени пространственная микроэкономическая выборка, состоящая из наблюдений одинаковых экономических единиц, которые проводятся последовательно и периодически. Панельные данные состоят из трех измерений: признак-объект-время. Их существенное преимущество заключается в том, с их помощью можно анализировать как временные ряды, так и пространственные выборки. Подобные данные используются при изучении бедности, безработицы, преступности, а также оценке результативности государственных социальных программ.
Готовые работы на аналогичную тему
Непараметрическая экономика
Непараметрическая экономика – это одно из ключевых бурно развивающихся эконометрических направлений. Непараметрическая экономика представляет собой раздел эконометрики, не требующий спецификации функциональной формы оцениваемого объекта. Вместо этого, сами данные формируют модель. Непараметрические методы более пригодны для исследования большого объема информации в случае малого количества переменных.
Непараметрическая экономика делает слабее параметрические предпосылки, что полезно в прикладных исследованиях.
Некоторые исследователи в непараметрическую экономику включают эконометрический анализ различных классов нечисловых математических объектов:
Так, статистика интервальных данных к элементам выборки относит не число, а интервал. Статистика интервальных данных изучает почти все задачи классической математической прикладной статистики, а именно задачи экспериментального планирования, регрессионного анализа, сопоставления альтернатив и принятия управленческих решений в условиях высокой неопределенности и т. п. Для этой научной отрасли разработана единая схема проведения исследования, которая включает расчет основных характеристик:
Что такое параметры модели в эконометрике
1.3. Эконометрика и возможности ее применения для анализа социально-экономических процессов
Экономико-математическая модель становится эконометрической и при ее построении и оценке используются эконометрические методы, если ставятся задачи:
1. получения с помощью этой модели количественных результатов на основе статистических данных;
2. количественной проверки гипотез, выдвигаемых экономической теорией.
Эконометрические модели применяются для изучения социально-экономических процессов и на макро- и на микро уровнях. Использование эконометрических методов является необходимым этапом построения количественной модели экономического объекта, независимо от того, для каких целей или в рамках какой дисциплины – исследования операций или, скажем, финансовой математики, модель строится (в результате, возникло даже такое понятие, как финансовая эконометрика).
Поведенческие и феноменологические модели
В связи с проблемой выбора структуры модели (спецификации), в зависимости от уровня знаний об объекте условно можно выделить два наиболее общих класса моделей:
1. поведенческие (behavioural models) ;
Поведенческие модели строятся только на основе наблюдений за поведением объекта (данных «вход-выход») и приближенно описывают (аппроксимируют) наблюдаемое поведение без какой либо априорной информации о внутренней структуре объекта (внутренних взаимосвязях между переменными). Структура и количество параметров устанавливаются в процессе построения модели. Параметры таких моделей могут не иметь какого-либо экономического смысла.
Одна из основных задач эконометрики – разработка методов построения поведенческих моделей.
Феноменологические модели (модели, основанные на знаниях) – это записанные в виде математических соотношений экономические законы, выведенные на основе экономической теории. Такие модели могут включать уравнения (дифференциальные или разностные), описывающие динамику процесса, статические балансовые соотношения (условия равновесия) и т. п., которые следуют из положений экономической теории. Как правило, структура уравнений таких моделей соответствует гипотезам экономической теории, а количество параметров заранее определено и ясен их экономический смысл.
Таким образом, построение эконометрической модели позволяет оценить степень достоверности гипотез, выдвигаемых экономической теорией, проверить их на практике. Это, в свою очередь, помогает выработать и обосновать рекомендации для проведения экономической политики, осуществить прогноз последствий принятия тех или иных экономических решений.
К классу поведенческих моделей можно отнести модели временных рядов.
Временным рядом называется последовательность упорядоченных во времени наблюдений некоторой величины, характеризующей экономический показатель.
Временные ряды – один из наиболее часто исследуемых объектов при изучении социально-экономических процессов и явлений, так как экономические данные чаще всего бывают представлены в виде временного ряда.
Примеры временных рядов в экономике
Пример 1. Данные за несколько лет об объеме еженедельных продаж запасных частей к сельскохозяйственной технике.
Пример 2. Данные о ежедневных котировках акций на фондовой бирже.
Пример 3. Данные о среднемесячных доходах в регионе за несколько лет.
Пример 4. Данные о ежемесячном потреблении фруктов за несколько лет.
Пример 5. Данные о среднемесячных уровнях инфляции.
Применяя эконометрические методы анализа временных рядов, можно построить математическую модель ряда, выявить закономерности его поведения в прошлом и на основе этого сделать обоснованный прогноз поведения экономического показателя в будущем. Такого типа модели относятся к поведенческим, так как они строятся только на основе наблюдений за поведением объекта, без какой либо информации или предположений относительно его структуры.
Анализ временного ряда позволяет ответить на следующие основные вопросы:
1. Существуют ли долгосрочные устойчивые тенденции роста (или снижения) показателя.
2. Существуют ли неслучайные регулярные и сезонные колебания показателя.
3. Какова степень влияния случайной составляющей (неопределенности) и ее характер.
4. Как будет вести себя изучаемый показатель в будущем (осуществить прогноз).
5. Оценить достоверность (надежность) прогноза.
Примеры типичных практических задач, для решения которых можно применять методы регрессионного анализа
Пример 1. Исходя из житейского опыта, и анализа данных, публикуемых риэлтерскими фирмами, можно предположить, что рыночная цена квартиры (объясняемая, эндогенная переменная) зависит от таких ее характеристик (объясняющих, экзогенных переменных), как количество комнат, общая и жилая площадь, площадь кухни, этаж, наличие проходных комнат, район города, кирпичный дом или панельный, средний уровень доходов населения данного региона, возраст квартиры, наличие балкона или лоджии, стоимость ремонта.
Применение эконометрических методов позволяет установить количественную взаимосвязь между ценой и характеристиками квартиры и ответить на вопрос, как изменится цена при изменении характеристик.
Пример 2. Цена товара в некоторый период (эндогенная переменная) зависит от объемов его поставок в этот период, цен конкурирующих товаров и, возможно, от времени года (сезона) (экзогенные переменные). С помощью регрессионной модели можно оценить, как изменится цена товара при изменении объемов поставок или цен конкурентов в зависимости от времени года.
Пример 3. Спрос на некоторый товар (эндогенная переменная) зависит от его цены, цен аналогичных товаров, производимых конкурентами, от реальных доходов потребителей в данном регионе (экзогенные переменные). Как изменится спрос при изменении экзогенных переменных?
Пример 4. Объем сбыта продукции зависит от затрат на рекламу. Модель позволяет оценить эту зависимость количественно и сделать прогноз сбыта при изменении затрат на рекламу в пределах определенной суммы, а также определить рациональный объем затрат на рекламу.
Пример 5. Регрессионный анализ позволяет установить функциональную зависимость эффективности работы предприятия (например, такого показателя, как рентабельность) от таких факторов, как удельный вес предприятия на рынке, расходы на маркетинг, научные исследования, качество товаров, объем инвестиций, зарплата менеджеров.
Пример 6. Как доходность акций некоторой корпорации зависит от доходности рыночного индекса (например, индекса РТС)?
Пример 7. Доходность финансовых активов зависит от темпов прироста валового продукта, уровня процентных ставок, уровня инфляции, уровня цен на нефть. Как изменится доходность конкретной ценной бумаги при изменении цен на нефть?
Пример 8. Оклад менеджера зависит от количества персонала в его подчинении, уровня квалификации и окладов менеджеров конкурирующих предприятий аналогичного профиля. Регрессионная модель позволяет ответить на вопрос, каким должен быть справедливый размер оклада руководителя вновь открывающегося филиала.
Пример 9. Торговая фирма имеет множество филиалов. Руководство фирмы хотело бы количественно оценить, как ежеквартальный товарооборот филиалов зависит от величины торговой площади и среднедневной интенсивности потока покупателей и на основе этого принять решение об открытии нового филиала. Обоснованное решение можно принять, используя методы регрессионного анализа.
При построении регрессионных моделей приходится решать следующие основные задачи:
1. определение вида функциональной связи между зависимой и независимыми (объясняющими) переменными (спецификация модели) с точностью до параметров;
2. формулировка гипотез относительно случайной составляющей;
3. подгонка некоторого, в общем случае не обязательно линейного, уравнения к заданному набору пространственных данных (оценка параметров модели);
4. проверка адекватности модели, то есть ее соответствия наблюдаемым данным.
Такие модели в большинстве случаев также можно отнести к классу поведенческих, поскольку их структура, взаимосвязи и взаимовлияние переменных, количество существенных переменных и параметров определяются в процессе построения регрессионной модели, основываясь в значительной степени только на анализе имеющихся пространственных данных. Заметим, впрочем, что при построении поведенческих моделей априорная информация так или иначе все-таки используется. Достаточно определить объект исследования, скажем, рынок недвижимости, (а не рынок ценных бумаг), и этого бывает достаточно, чтобы в принципе выделить основные факторы, влияющие на процессы установления рыночных цен на этом рынке (но, к сожалению, не структуру функциональной связи).
Применение регрессионного анализа для решения практических задач позволяет ответить на следующие основные вопросы:
1. установить вид функциональной зависимости между эндогенной и экзогенной переменными (определить спецификацию модели);
2. оценить степень влияния каждой независимой переменной, выявить существенные и несущественные независимые переменные;
3. оценить роль и степень влияния на изучаемый показатель факторов, не учитываемых явно в модели;
4. осуществить прогноз эндогенной переменной при изменении значений экзогенных переменных;
Построив эконометрическую модель, скажем, для анализа рынка недвижимости (см. пример 1 ), устанавливающую количественную зависимость рыночной цены квартиры от вышеперечисленных и возможно, других факторов, аналитик получает в распоряжение мощный инструмент анализа, с помощью которого можно определить, справедливо ли оценена та или иная квартира (возможно недооценена или переоценена исходя из ее характеристик), как изменится цена при изменении той или иной независимой переменной, характеризующей рыночную среду, оказывающую влияние на цены недвижимости и т. д. и т.п., что в свою очередь позволит существенно повысить обоснованность принимаемых решений.
Модели множественной регрессии используются для изучения многих экономических процессов.
Системы одновременных уравнений




Данная модель построена исходя из гипотетических предположений относительно вида зависимостей между переменными, основываясь на предпосылках экономической теории и относится к классу феноменологических моделей.
Для того, чтобы ее можно было применить в количественных расчетах, необходимо решить следующие основные задачи:
1. оценить параметры модели исходя из реальных данных о развитии конкретной экономической системы;
2. проверить, адекватно ли данная модель описывает систему.
Эконометрические методы позволяют «настроить» параметры модели на конкретный набор данных ( идентифицировать модель) и решить множество связанных с этим вопросов. Отметим, что в настоящее время разработаны большие эконометрические модели как отдельных секторов, так и национальных экономик в целом (например, эконометрическая модель экономики США), содержащие сотни одновременных уравнений. Эти модели используются для прогноза развития экономической системы, анализа последствий правительственной политики на уровне государства, региона, отдельных секторов и т.д., выработки рациональных управляющих воздействий (решений).
Таким образом, исходя из выше приведенных рассуждений, можно охарактеризовать эконометрику в узком смысле как технологию (набор методов, способов, приемов, подходов, рекомендаций и формальных инструкций) решения задач идентификации параметрических моделей экономических объектов (процессов, систем, явлений) по данным наблюдений с использованием вероятностно-статистических методов.
Эконометрика в широком смысле – это сочетание искусства и технологии установления вида и количественной оценки функциональных зависимостей между экономическими переменными, характеризующими поведение экономического объекта, по наблюдаемым данным с применением любого современного математического аппарата.
Подчеркнем практические преимущества построения эконометрических моделей.
1. Возможность компактного и наглядного описания процесса.
2. Упорядочение и оценка значимости информации.
3. Прогноз поведения объекта.
4. Изучение возможных сценариев развития.
5. Выбор оптимального решения (наилучшего среди возможных).
6. Эффективное применение современных информационных технологий.
Виды эконометрических моделей
Главным инструментом эконометрического исследования является модель. Выделяют три основных класса эконометрических моделей:
Моделью временных рядов называется зависимость результативной переменной от переменной времени или переменных, относящихся к другим моментам времени.
К моделям временных рядов, характеризующих зависимость результативной переменной от времени, относятся:
а) модель зависимости результативной переменной от трендовой компоненты или модель тренда;
б) модель зависимости результативной переменной от сезонной компоненты или модель сезонности;
в) модель зависимости результативной переменной от трендовой и сезонной компонент или модель тренда и сезонности.
К моделям временных рядов, характеризующих зависимость результативной переменной от переменных, датированных другими моментами времени, относятся:
а) модели с распределённым лагом, объясняющие вариацию результативной переменной в зависимости от предыдущих значений факторных переменных;
б) модели авторегрессии, объясняющие вариацию результативной переменной в зависимости от предыдущих значений результативных переменных;
в) модели ожидания, объясняющие вариацию результативной переменной в зависимости от будущих значений факторных или результативных переменных.
Кроме рассмотренной классификации, модели временных рядов делятся на модели, построенные по стационарным и нестационарным временным рядам.
Стационарным временным рядом называется временной ряд, который характеризуется постоянными во времени средней, дисперсией и автокорреляцией, т. е. данный временной ряд не содержит трендовой и сезонной компонент.
Нестационарным временным рядом называется временной ряд, который содержит трендовую и сезонную компоненты.
Определение. Моделью регрессии с одним уравнением называется зависимость результативной переменной, обозначаемой как у, от факторных (независимых) переменных, обозначаемых как х1,х2,…,хn. Данную зависимость можно представить в виде функции регрессии или модели регрессии:
где β1…βk – параметры модели регрессии.
Можно выделить две основных классификации моделей регрессии::
а) классификация моделей регрессии на парные и множественные регрессии в зависимости от числа факторных переменных;
б) классификация моделей регрессии на линейные и нелинейные регрессии в зависимости от вида функции f(x,β).
В качестве примеров моделей регрессии с одним уравнением можно привести следующие модели:
а) производственная функция вида Q=f(L,K), выражающая зависимость объёма производства определённого товара (Q) от производственных факторов – от затрат капитала (К) и затрат труда (L);
б) функция цены Р=f(Q,Pk), характеризующая зависимость цены определённого товара (Р) от объема поставки (Q) и от цен конкурирующих товаров (Pk);
в) функция спроса Qd=f(P,Pk,I), характеризующая зависимость величины спроса на определённый товар (Р) от цены данного товара (Р), от цен товаров-конкурентов (Pk) и от реальных доходов потребителей (I).
Системой одновременных уравнений называется модель, которая описывается системами взаимозависимых регрессионных уравнений.
Системы одновременных уравнений могут включать в себя тождества и регрессионные уравнения, в каждое из которых могут входить не только факторные переменные, но и результативные переменные из других уравнений системы.
Регрессионные уравнения, входящие в систему одновременных уравнений, называются поведенческими уравнениями. В поведенческих уравнениях значения параметров являются неизвестными и подлежат оцениванию.
Основное отличие тождеств от регрессионных уравнений заключается в том, что их вид и значения параметров известны заранее.
Примером системы одновременных уравнений является модель спроса и предложения, в которую входит три уравнения:
а) уравнение предложения: =а0+а1*Рt+a2*Pt-1;
б) уравнение спроса: =b0+b1* Рt+b2*It;
в) тождество равновесия: QSt = Qdt,
где QSt – предложение товара в момент времени t;
Qdt – спрос на товар в момент времени t;
Рt – цена товара в момент времени t;
Pt-1 – цена товара в предшествующий момент времени (t-1);
It– доход потребителей в момент времени.
В модели спроса и предложения выражаются две результативные переменные:
а) Qt– объём спроса, равный объёму предложения в момент времени t;
б) Pt– цена товара в момент времени t.
Понятие эконометрической модели и последовательность ее построения



Хубулава Ное Михайлович
Учебник для студентов экономического профиля
всех специальностей и всех форм обучения, а также
на специалистов, занимающихся проблемами
экономического измерения, прогнозирования
Подписано в печать 10.05.2005. Формат 60×84 1/14.
Бумага офсетная. Печать офсетная. Уч. изд.
Лист 8,1. Тираж 5000.

Москва, Енисеевская 36.
— изучать реальное состояние объектов или процессов, выявлять и оценивать наиболее существенные факторы, определяющие поведение объекта исследования;
— прогнозировать изменение состояния объекта моделирования во времени.
Эконометрика как наука сформировалась и получила развитие на стыке экономической теории, математической и экономической статистики.
Экономическая теория предоставляет для эконометрики научное обоснование наличия и формы связи между явлениями и процессами. Однако, в отличие от экономической теории, эконометрику интересует не качественный анализ, а количественная оценка связей.
Эта оценка основывается на использовании методов математической статистики, и, прежде всего, корреляционно-регрессионного анализа. Информационной базой для построения моделей являются статистические данные. При построении эконометрической модели крайне важно знать способы получения и методики расчета показателей, поскольку в противном случае полученные на основе моделей выводы могут оказаться неточными. Кроме того, наличие статистической информации определяет конкретный состав используемых в модели показателей.
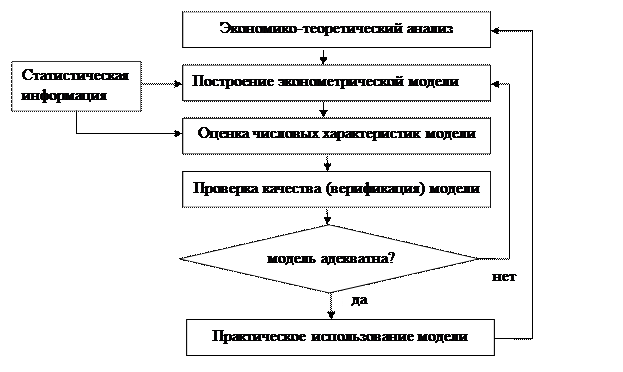
Процесс построения эконометрической модели можно представить следующим образом:
1.2. Эконометрическая модель: основные понятия.
Эконометрическая модель включает два вида переменных.
1. Переменные, характеризующие те экономические явления и процессы, которые требуется объяснить. Такие переменные принято называть зависимыми или объясняемыми и обозначать Y.
2. Переменные, характеризующие те процессы и явления, которые влияют на значение объясняемой переменной. Они называются независимыми или объясняющими и обозначаются Х1, Х2, Х3 и т.д.
Математически связь между зависимой и независимой переменными записывается в виде функции:
При наличии линейной связи между зависимой и независимой переменными, модель приобретает следующий вид:
В процессе эконометрического моделирования оценивается ожидаемое теоретическое значение зависимой переменной уt на основе выборочных данных:
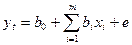
Например, при анализе стоимости жилья собрана информация по двум сотням различных квартир. По каждой их них определена цена квадратного метра, этаж, количество комнат и пр. Значение yt1 будет представлять собой цену квадратного метра в первой квартире, yt2 — во второй квартире так далее вплоть до yt200.
Аналогично определяются значения независимых переменных. Так, значение x11 будет представлять собой порядковый номер этажа в первой квартире, x12 — во второй квартире, значение x21 — количество комнат в первой квартире, x22 — во второй и т.д.
По результатам эконометрического анализа определяется усредненное влияние каждой из независимых переменных на зависимую посредством расчета величин b0, b1, b2 и т.д. Они называются параметрами модели.
Процедура оценивания эконометрических моделей, интерпретация и применение полученных результатов будут рассмотрены в последующих темах курса.