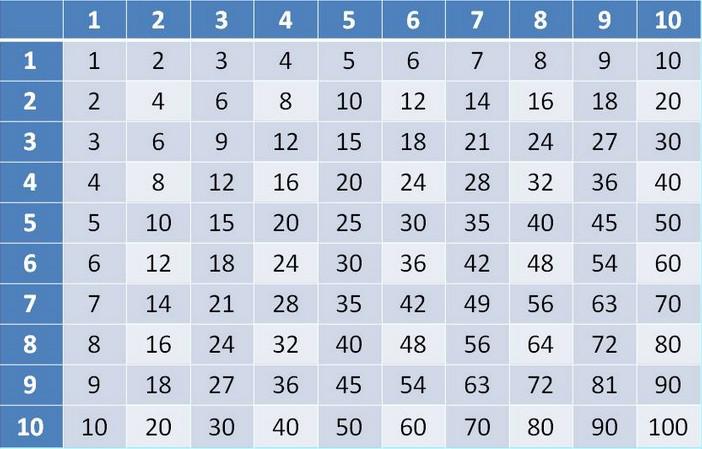
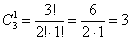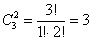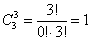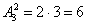что значит считай без повторений

Размещения

п.1. Размещения без повторений

Например:
Для создания 3-значного пароля используются символы из алфавита <+,*,A. 2>.
Сколько всего паролей без повторения символов можно составить?
По условию n = 5, k = 3. Рассматриваем размещение 5 символов по 3 позициям без повторений: \(\mathrm< A_5^3=\frac<5!><(5-3)!>=5\cdot 4\cdot 3 = 60 >\)
Всего 60 паролей.
Результат можно получить непосредственно из правила произведения. Действительно, на первой позиции – 5 вариантов символов, на второй – 4 оставшихся, на третьей – 3 оставшихся. Итого, по правилу произведения: 5 · 4 · 3 = 60 паролей.

п.2. Размещения с повторениями

п.3. Примеры

Пример 1. Исследуйте различие между перестановкой без повторений и размещением без повторений 〈3,2〉-выборок для трёх разноцветных фишек. Изобразите полученные решения.

Рассматриваем фишки:

1) Для перестановок, 〈3,3〉-выборок, получаем:

В каждом ряду – отдельная перестановка. Видно, как образуется факториал. Для каждой отдельной фишки – одна перестановка. Для каждой пары фишек – две перестановки: 2 · 1. Когда добавляем третью, получаем: 3 · 2 · 1 Итого: P3 = 3 · 2 · 1 = 6 перестановок.

2) Для размещений без повторений, 〈3,2〉-выборок, получаем:

В каждом ряду – отдельное размещение. В первом столбце слева – 3 варианта по цвету. Во втором столбце остается только 2 варианта. Итого: \(\mathrm\) размещений.

Пример 2. Исследуйте перестановки без повторений и размещения для 〈4,3〉 выборок и для 〈4,2〉 выборок без повторений из 4 разноцветных фишек.
Изобразите полученные решения.

Рассматриваем фишки:

В каждом ряду – отдельная перестановка. Итого: P4=4·3·2·1=24 перестановки.

В каждом ряду – отдельное размещение. Итого: \(\mathrm\) размещения.

В каждом ряду – отдельное размещение. Итого: \(\mathrm\) размещений.

Пример 3. Исследуйте различие между перестановкой с повторениями и размещением с повторениями. Сделайте вывод.
Перестановка с повторениями: сколько слов можно получить, переставляя буквы в слове «МАМА»? Запишите все эти слова в лексикографическом порядке.
Размещение с повторениями: сколько 4-буквенных слов можно получить, используя две буквы: «М» и «А»? Запишите все эти слова в лексикографическом порядке.

1) Для перестановки с повторениями получаем: \begin \mathrm< a_1=M,k_1=2,\ \ \ a_2=A,k_2=2 >\\ \mathrm< k=k_1+k_2=2+2=4 >\\ \mathrm< P_4(2;2)=\frac<4!><2!\cdot 2!>=\frac<24><2\cdot 2>=6 > \end Все 6 слов в лексикографическом порядке:

Вывод: вариантов для размещения с повторениями получается больше, т.к. они включают слова с одной, тремя и четырьмя «М» и «А». А в перестановки с повторениями входят только слова с двумя «М» и двумя «А».

Пример 4. В базе данных с номерами телефонов содержатся все 7-значные номера.
1) Сколько в книге номеров, в которых цифры не повторяются?
2) Сколько в книге всего номеров?
3) Сколько в книге номеров, у которых 4 последних цифры одинаковые?
4) Сколько в книге номеров, у которых 4 последних цифры одинаковые, а 3 первых цифры отличаются от 4 последних?
1) Цифр – всего 10:

Источник

Сколько повторений делать в упражнениях?

Сколько повторений делать в подходе – это очень важный вопрос. От числа повторений зависит результат, который Вы получите от занятий. В этой статье я постараюсь максимально точно ответить на этот вопрос. И Вы сможете правильно определять норму повторов, основываясь на собственных целях.

Для начала ознакомьтесь с этой схемой. А ниже я дам все объяснения.

Какое число повторений является правильным?

Всё зависит от цели занятий, Вашего возраста и уровня подготовки.

Принято считать, что для роста силы нужно выполнять 1-6 повторений с большим весом. Для роста мышечной массы необходимо делать 6-12 повторений. А для улучшения мышечного рельефа – 12-15 и более повторений.

В общем, всё это недалеко от истины. Но когда речь заходит о практике, возникает много нюансов. И суть, как это часто бывает, состоит в мелочах. В этих самых нюансах.

Для начала сделаем следующее. С одной стороны я предлагаю чётко разделять разные зоны повторений. С другой стороны, отказываюсь от чёткого разделения этих зон.

Что такое повторный максимум?

Этот показатель поможет лучше понимать тему. Его обычно обозначают ПМ или просто указывают, что вес равен 100%.

Повторный максимум – это конкретный вес, который Вы можете поднять в данном упражнении только один раз. Обязательно технически чисто (без читинга и других хитростей). Добавление к этому весу даже 100 г делает этот вес неподъёмным для Вас.

Если написано, что вес равен 90%, значит, речь идёт о весе, составляющем 0,9 от повторного максимума. Если в приседаниях со штангой Ваш повторный максимум составляет 70 кг, значит, 90% от него будет составлять 63 кг. Уяснили? Идём дальше.

Число повторений. Чётко разделяем зоны.

1-3 повторения

Этим числом повторов увеличивают разовую силу. Здесь мы используем самые тяжёлые веса (90-105% от максимума, но бывают исключения – как-нибудь расскажу о методике низкоповторного взрывного тренинга с небольшими весами). Не удивляйтесь, в силовых тренировках пауэрлифтинга часто встречается значение 105%. Это нормальная практика, позволяющая атлетам быстро достигать новых результатов.

В этом диапазоне мощно развиваются такие параметры, как координация движений (немаловажная вещь для развития разовой мышечной силы) и иннервация двигательных единиц (это группы мышечных клеток, иннервируемые одним мотонейроном).

Большие веса мгновенно заставляют тело принимать оптимальные положения и проявлять оптимальную биомеханику.

А двигательные единицы вообще очень интересная вещь. Чисто силовой тренинг «учит» мышцы задействовать как можно больше двигательных единиц одновременно, в одном повторении. Эта синхронизация и проявляется как разовая сила.

Все мы отличаемся друг от друга количеством мышечных клеток, входящих в одну двигательную единицу. Это определяется генетикой. Разумеется, более физически сильными являются люди, у которых в каждой двигательной единице больше мышечных волокон. И у которых очень многие двигательные единицы работают синхронно. См. также как устроены мышцы.

Данный метод лучше всего развивает белые мышечные волокна.

4-6 повторений

Такое число повторений выполняют в подходах для развития мощности мышц и взрывной силы (см. также плиометрическая тренировка). Обычно при этом используют веса 80-85% от повторного максимума.

Подходы из 4-6 повторений оптимальны для развития взрывной силы и мощности движений. Однако рекорды в разовых повторениях этот метод растит уже не так эффективно, как тренировка с 90-105%, несмотря на то, что тоже хорошо развивает белые мышечные волокна.

6-8 повторений

Это очень удобное и комфортное число повторов для роста мышечной массы. Оптимальный вес – 70-80% от повторного максимума. Помню, что добился наибольшего прогресса в приседаниях со штангой на массу именно на этом числе повторений. Более высокое число повторений приводило к острой нехватке кислорода и преждевременному прекращению подхода.

Считается, что этот диапазон оптимален для развития миофибриллярной гипертрофии мышц. То есть развиваются (увеличиваются в толщину) мышечные миофибриллы (сократительные элементы мышечных клеток). В основном на это количество повторений хорошо отзываются белые мышечные волокна.

Диапазон очень хорош и комфортен. Однако по ощущениям, если “сидеть” только на нём постоянно, не происходит развития выносливости (она буквально испаряется) и даже обычная пробежка на 2-3 км или пара раундов на ринге становятся жестоким испытанием для дыхалки и сердца.

9-12 повторений

Многие считают, что это количество слишком велико для роста мышечной массы и относят этот диапазон к выносливости. Ведь здесь мы имеем дело с весами порядка 65-70% от повторного максимума. При тренировках с такими весами активно включаются в работу и красные мышечные волокна.

Однако, практика занятий и некоторые исследования говорят о значительном массонаборном эффекте в диапазоне от 10 до 18 повторений. Это входит в противоречие с мнением убеждённых сторонников чисто силового тренинга, нацеленных на 6-8 повторений. К тому же после многих лет занятий на низком числе повторений тренировки на 12 и более повторов очень не комфортны. Многие атлеты путают это чувство дискомфорта с отсутствием эффекта.

В диапазоне от 10 до 18 повторений в мышцах, действительно, не наблюдается активного роста миофибрилл в толщину. Однако, наблюдается серьёзное увеличение объёма саркоплазмы, напрямую влияющее на объём мышц и силовую выносливость. Разовые сократительные способности мышц это не увеличивает, но значительно растёт функциональная составляющая (способность работать интенсивно и долго). Поэтому мнение убеждённых сторонников можно спокойно подвинуть и расширить, если речь идёт именно о росте мышечной массы.

К тому же не стоит забывать, что на рост мышечной массы влияет множество тренировочных параметров: время под нагрузкой (и, соответственно, число подходов), рост рабочего веса и т.д.

12-15 повторений

Считается оптимальным числом для улучшения формы и рельефа мышц. Обычно здесь используют веса в диапазоне 55-65% от повторного максимума. В мышцах работают, главным образом, красные мышечные волокна.

Форму и рельеф этот диапазон, действительно, улучшает. Но многое зависит и от питания. Если сделать его массонаборным, будет очень хорошо расти масса.

15-25 и более повторений

По устоявшимся представлениям это зона почти исключительно роста выносливости мышц и улучшения их рельефа. Если работать с железом, то при таком числе повторов используются веса в районе 55% от повторного максимума и ниже. В мышцах работают почти исключительно красные мышечные волокна, как раз и отвечающие за выносливость. А также за сжигание жиров.

Обязательно имейте в виду, что такая тренировка очень серьёзно бьёт по разовой силе, быстро её снижая.

Именно по этой причине люди, практикующие так называемый ЗОЖ – регулярный длительный бег и простейшие упражнения с собственным весом на много повторений, а зачастую и радикальные формы вегетарианства (боже упаси!) так не любят «железо» или ограничивают его до минимума. И совершенно напрасно, между прочим! Железо – очень мощный стимулятор здоровья и, к сожалению, предмет огромных заблуждений среди людей старшего поколения…

Ну что же, мы прошлись по всему разумному диапазону повторений в силовых упражнениях. Теперь посмотрим, почему стоит отойти от чётких границ этих диапазонов.

Реакция мышц и всего организма на эти диапазоны включает разные механизмы и адаптации. И зачастую определённая адаптация начинает проявляться в одной зоне, максимально проявляется в другой, и порой её признаки присутствуют в третьей и т.д. зонах повторений. То есть многие параметры не связаны с конкретным числом повторений однозначно.

Когда речь идёт о чисто силовом тренинге на разы, то лучшим способом здесь будет выполнение именно разовых повторов с максимальными весами. Однако, даже если Вы будете тренироваться на 6-8 повторений, разовая сила тоже будет расти. Но не так быстро. Ведь 6-8 повторений не являются оптимальными для этого.

Отдельно стоит вспомнить о тренировках на рельеф, когда нужно «сжечь» лишние килограммы. Вроде бы здесь надо просто делать много повторений. А вот и не обязательно!

Существует много методов тренировки, позволяющих быстро сжигать жир, тренируясь с относительно большими весами и невысоким числом повторений (8-12). Речь о таких методах, как круговой тренинг, комбинированные подходы, суперсеты и т.д.

Какое число повторений нужно Вам?

Если Вы новичок (плохая форма и нет опыта занятий, плюс, возможно, лишние килограммы)

Занимайтесь простыми упражнениями с собственным весом на 15 и более повторений. Старайтесь увеличить это число до 40-50 и более. Примеры упражнений: приседания, отжимания с коленей, скручивания, наклоны вперёд, подтягивания на низкой перекладине и т.д.

Если Вы начинающий (тренируетесь меньше 3-6 месяцев)

Выполняйте силовые упражнения на 12-15 повторений. Старайтесь постепенно увеличивать рабочий вес.

Если Вы имеете средний уровень подготовки (тренируетесь от 6 до 12 месяцев)

Вам следует задуматься о периодизации тренировок. Это простое чередование комплексов упражнений с разным числом повторений. Вам однозначно пойдут на пользу и 6-8, и 12-15, и 15-25 повторений. И лучше бы их разделить на разные комплексы упражнений, выполняемые в разные месяцы года.

Это же я могу рекомендовать и всем опытным. Но диапазон повторений для Вас ещё шире – с 1 до 50 в разных программах в течение года.

Если у Вас лишние килограммы (но Вы хоть как-то подвижны)

Начните практиковать высокоповторные простые упражнения с собственным весом. Делайте по 20-40 и более приседаний за подход. Делайте много наклонов (20 и более за подход). Именно этот метод прекрасно зарекомендовал себя в моём тренинге Сушка для умных.

Если у Вас недостаток веса или Вы эктоморф (и уже есть хотя бы 3 месяца опыта занятий)

Занимайтесь в подходах на 4-6 или 6-8 повторений. Это позволит максимально быстро растить мышцы и набирать вес. Никакие отжимания и бег здесь не помогут. Нужен именно силовой тренинг и очень сытное питание. И между подходами отдыхайте побольше. Тренировка получится более длинной, зато и “мясо” будет нарастать эффективно.

Если Вы старше 50 лет

Рекомендуется не использовать в тренировках низкое количество повторений (1-6). Точнее, использовать редко, в качестве пиковых тренировок раз в 2-4 недели. Тем не менее, вовсе отказываться от силовых занятий не стоит. В течение года у Вас должно быть 2-3 комплекса по 1-2 месяца с числом повторений от 6 до 10. Это крайне важно именно в силу возраста, когда активно теряется мышечная масса, а с нею и остатки здоровья.

Желаю успешных занятий! Вопросы и комментарии приветствуются.

Источник

Перестановки, размещения и сочетания. Формулы.

Чтобы в материале было легче ориентироваться, добавлю содержание данной темы:

Введение. Множества и выборки.

В этой теме рассмотрим основные понятия комбинаторики: перестановки, сочетания и размещения. Выясним их суть и формулы, по которым можно найти их количество.

Для работы нам понадобятся кое-какие вспомогательные сведения. Начнём с такого фундаментального математического понятия как множество. Подробно понятие множества было раскрыто в теме «Понятие множества. Способы задания множеств».

Очень краткий рассказ про множества: показать\скрыть

Заметьте, что в определении выборки ничего не сказано про повторения элементов. В отличие от элементов множеств, элементы выборки могут повторяться.

Запись «n!» (читается «эн факториал») обозначает произведение всех чисел от 1 до n, т.е.

Нас же интересует общее количество этих размещений. Согласно формуле (1) количество размещений без повторений из 5 элементов по 3 будет таким:

Т.е. можно составить 60 трёхсимвольных слов, буквы которых не будут повторяться.

Следовательно, из заданных цифр можно составить 243 пятизначных числа.

В морозилке лежат пять порций мороженого от различных фирм. Сколькими способами можно выбрать порядок их съедения?

Следовательно, существует 120 порядков выбора очередности съедения.

Перестановки с повторениями

Общее количество перестановок с повторениями определяется формулой:

Следовательно, общее количество искомых слов равно 105.

В корзине размещены карточки, на которых написаны целые числа от 1 до 10. Из корзины вынимают 4 карточки и суммируют числа, написанные на них. Сколько различных наборов карточек можно вытащить из корзины?

Следовательно, общее количество искомых наборов равно 210.

Представьте себе, что мы находимся на конфетном заводе, – прямо возле конвейера, по которому движутся конфеты четырёх сортов. Мы запускаем руки в этот поток и вытаскиваем двадцать штук. Сколько всего различных «конфетных комбинаций» может оказаться в горсти?

Следовательно, общее количество искомых комбинаций равно 1771.

Заметили ошибку, опечатку, или некорректно отобразилась формула? Отпишите, пожалуйста, об этом в данной теме на форуме (регистрация не требуется).

Источник

1.3.1. Перестановки, сочетания и размещения без повторений

Начнём с хвоста заголовка – что значит «без повторений»? Это значит, что в данном параграфе будут рассматриваться множества, которые состоят из различных объектов, либо которые считаются таковыми по смыслу задачи.

Представьте, что перед вами на столе слева направо выложены:
яблоко / груша / банан

Вопрос первый: сколькими способами их можно переставить?

Одна комбинация уже записана выше и с остальными проблем не возникает:

яблоко / банан / груша
груша / яблоко / банан
груша / банан / яблоко
банан / яблоко / груша
банан / груша / яблоко

Итого: 6 комбинаций или 6 перестановок.

Хорошо, здесь не составило особого труда перечислить все возможные случаи, но как быть, если предметов больше? Уже с четырьмя различными фруктами количество комбинаций значительно возрастёт! Пожалуйста, откройте Приложение Основные формулы комбинаторики и в пункте № 2 найдите формулу количества перестановок. Никаких мучений – 3 объекта можно переставить: 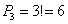способами.

Вопрос второй: сколькими способами можно выбрать а) один фрукт, б) два фрукта, в) три фрукта, г) хотя бы один фрукт?

а) Один фрукт можно выбрать, очевидно, тремя способами – взять либо яблоко, либо грушу, либо банан. Формальный подсчёт проводится по формуле количества сочетаний (см. тот же п.2 Приложения):

Запись 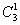следует читать и понимать так: «сколькими способами можно выбрать 1 фрукт из трёх?».

б) Перечислим все возможные сочетания двух фруктов:

яблоко и груша;
яблоко и банан;
груша и банан.

Количество комбинаций легко проверить по той же формуле:

Запись 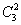понимается аналогично: «сколькими способами можно выбрать 2 фрукта из трёх?».

в) И, наконец, три фрукта можно выбрать единственным способом:

Следует отметить, что формула количества сочетаний сохраняет смысл и для пустой выборки:
способом можно выбрать ни одного фрукта – собственно, ничего не взять и всё. Но это явно не про студенток J

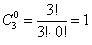
г) Сколькими способами можно взять хотя бы один фрукт? Условие «хотя бы один» подразумевает, что нас устраивает 1 фрукт (любой) или 2 любых фрукта (любые) или все 3 фрукта:
способами можно выбрать хотя бы один фрукт.

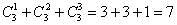
…внимательные читатели уже кое о чём догадались. Но о смысле знака «плюс» позже.

И для ответа на третий вопрос мне требуется два добровольца…, ну что же, раз никто не хочет, тогда буду вызывать к доске =)

Вопрос третий: сколькими способами можно раздать по одному фрукту Даше и Наташе?

Для того чтобы раздать два фрукта, сначала нужно их выбрать. Согласно пункту «бэ» предыдущего вопроса, сделать это можно 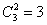способами, перепишу их заново:

яблоко и груша;
яблоко и банан;
груша и банан.

Но комбинаций сейчас будет в два раза больше. Рассмотрим, например, первую пару фруктов:
яблоком можно угостить Дашу, а грушей – Наташу;
либо наоборот – груша достанется Даше, а яблоко – Наташе.

И такая перестановка возможна для каждой пары фруктов.

В данном случае работает формула количества размещений:

Она отличается от формулы 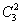тем, что учитывает не только количество способов, которым можно выбрать несколько объектов, но и все перестановки объектов в каждой возможной выборке. Так, в рассмотренном примере, важно не только то, что можно просто выбрать, например, грушу и банан, но и то, как они будут распределены (размещены) между Дашей и Наташей.

Пожалуйста, ещё раз внимательно перечитайте пункт № 2 Приложения Основные формулы комбинаторики и постарайтесь хорошо уяснить разницу между перестановками, сочетаниями и размещениями. В простых случаях легко пересчитать все возможные комбинации вручную, но чаще всего это становится трудноподъёмной задачей, именно поэтому и нужно понимать смысл формул.

Теперь остановимся на каждой комбинации подробнее:

Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!

С наилучшими пожеланиями, Александр Емелин

Источник

Как быстро считать в уме: приемы устного счета больших чисел

Устный счет – занятие, которым в наше время себя утруждает все меньшее количество людей. Гораздо проще достать калькулятор на телефоне и вычислить любой пример.

Но так ли это на самом деле? В этой статье мы представим математические лайфхаки, которые помогут научиться быстро складывать, вычитать, умножать и делить числа в уме. Причем оперируя не единицами и десятками, а минимум двухзначными и трехзначными числами.

После освоения методов из этой статьи идея лезть в телефон за калькулятором уже не покажется такой хорошей. Ведь можно не тратить время и посчитать все в уме гораздо быстрее, а заодно размять мозги и произвести впечатление на окружающих (противоположного пола).

Итак, добро пожаловать в увлекательный мир вычислений! Мы собрали советы от наших авторов о том, как улучшить устный счет и стать математическим героем и гением. Кстати, если вам интересна математика, вы можете почитать статью «Пределы для чайников» в нашем блоге.

Предупреждаем! Если вы обычный человек, а не вундеркинд, то для развития навыка счета в уме понадобятся тренировки и практика, концентрация внимания и терпение. Сначала все может получаться медленно, но потом дело пойдет на лад, и вы сможете быстро считать в уме любые числа.

Гаусс и устный счет

Карл Фридрих Гаусс

Одним из математиков с феноменальной скоростью устного счета был знаменитый Карл Фридрих Гаусс (1777-1855). Да-да, тот самый Гаусс, который придумал нормальное распределение.

По его собственным словам, он научился считать раньше, чем говорить. Когда Гауссу было 3 года, мальчик взглянул на платежную ведомость своего отца и заявил: «Подсчеты неверны». После того как взрослые все перепроверили, выяснилось, что маленький Гаусс был прав.

В дальнейшем этот математик достиг немалых высот, а его труды до сих пор активно используются в теоретических и прикладных науках. До самой смерти большую часть вычислений Гаусс производил в уме.

Здесь мы не будем заниматься сложными расчетами, а начнем с самого простого.

Сложение чисел в уме

Чтобы научиться складывать в уме большие числа, нужно уметь безошибочно складывать числа до 10. В конечном счете любая сложная задача сводится к выполнению нескольких тривиальных действий.

Чаще всего проблемы и ошибки возникают при сложении чисел с «переходом через 10». При сложении (да и при вычитании) удобно применять технику «опоры на десяток». Что это? Сначала мы мысленно спрашиваем себя, сколько одному из слагаемых не хватает до 10, а потом прибавляем к 10 оставшуюся до второго слагаемого разность.

Например, сложим числа 8 и 6. Чтобы из 8 получить 10, не хватает 2. Затем к 10 останется прибавить 4=6-2. В итоге получаем: 8+6=(8+2)+4=10+4=14

Основная хитрость со сложением больших чисел – разбить их на разрядные части, а потом сложить эти части между собой.

Пусть нам нужно сложить два числа: 356 и 728. Число 356 можно представить как 300+50+6. Аналогично, 728 будет иметь вид 700+20+8. Теперь складываем:

356+728=(300+700)+(50+20)+(8+6)=1000+70+14=1084

Вычитание чисел в уме

Вычитание чисел тоже будет даваться легко. Но в отличие от сложения, где каждое число разбивается на разрядные части, при вычитании «разбить» нужно только то число, которое мы отнимаем.

Например, сколько будет 528-321? Разбиваем число 321 на разрядные части и получаем: 321=300+20+1.

Теперь считаем: 528-300-20-1=228-20-1=208-1=207

Попробуйте визуализировать процессы сложения и вычитания. В школе всех учили считать в столбик, то есть сверху вниз. Один из способов перестроить мышление и ускорить счет – считать не сверху вниз, а слева направо, разбивая числа на разрядные части.

Умножение чисел в уме

Умножение – это многократное повторение числа. Если нужно умножить 8 на 4, это значит, что число 8 нужно повторить 4 раза.

Так как все сложные задачи сводятся к более простым, нужно уметь умножать все однозначные числа. Для этого существует отличный инструмент – таблица умножения. Если вы не знаете эту таблицу на зубок, то мы настоятельно рекомендуем первым делом выучить ее и только потом приниматься за практику устного счета. К тому же учить там, по сути, нечего.

Умножение многозначных чисел на однозначные

Сначала потренируйтесь в умножении многозначных чисел на однозначные. Пусть нужно умножить 528 на 6. Разбиваем число 528 на разряды и идем от старшего к младшему. Сначала умножаем, а потом складываем результаты.

528=500+20+8

528*6=500*6+20*6+8*6=3000+120+48=3168

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Умножение двузначных чисел

Здесь тоже нет ничего сложного, только нагрузка на краткосрочную память немного больше.

Перемножим 28 и 32. Для этого сведем всю операцию к умножению на однозначные числа. Представим 32 как 30+2

28*32=28*30+28*2=20*30+8*30+20*2+8*2=600+240+40+16=896

Еще один пример. Умножим 79 на 57. Это значит, что на нужно взять число «79» 57 раз. Разобьем всю операцию на этапы. Сначала умножим 79 на 50, а потом – 79 на 7.

Умножение на 11

Вот хитрый прием быстрого устного счета, который поможет умножить любое двузначное число на 11 с феноменальной скоростью.

Проверим и умножим 54 на 11.

Возведение в квадрат

С помощью другого интересного приема устного счета можно легко и быстро возводить двузначные числа в квадрат. Особенно просто это делать с числами, которые заканчиваются на 5.

Результат начинается с произведения первой цифры числа на следующую за ней по иерархии. То есть, если эту цифру обозначить через n, то следующей за ней по иерархии цифрой будет n+1. Результат заканчивается на квадрат последней цифры, то есть квадрат 5.

Проверим! Возведем в квадрат число 75.

Раньше все считали без калькуляторов

Деление чисел в уме

Осталось разобраться с делением. По сути, это операция, обратная умножению. С делением чисел до 100 никаких проблем вообще возникать не должно – ведь есть таблица умножения, которую вы знаете на зубок.

Деление на однозначное число

При делении многозначных чисел на однозначное необходимо выделить максимально большую часть, которую можно разделить с помощью таблицы умножения.

Например, есть число 6144, которое нужно разделить на 8. Вспоминаем таблицу умножения и понимаем, что на 8 будет делиться число 5600. Представим пример в виде:

6144:8=(5600+544):8=700+544:8

Далее из числа 544 также выделяем максимально большое число, которое делится на 8. Имеем:

544:8=(480+64):8=60+64:8

Осталось разделить 64 на 8 и получить результат, сложив все результаты деления

6144:8=700+60+8=768

Деление на двузначное число

При делении на двузначное число нужно пользоваться правилом последней цифры результата при умножении двух чисел.

При умножении двух многозначных чисел последняя цифра результата умножения всегда совпадает с последней цифрой результата умножения последних цифр этих чисел.

Например, умножим 1325 на 656. По правилу, последняя цифра в получившемся числе будет 0, так как 5*6=30. Действительно, 1325*656=869200.

Теперь, вооружившись этой ценной информацией, рассмотрим деление на двузначное число.

Сколько будет 4424:56?

Первоначально будем пользоваться методом «подгона» и найдем пределы, в которых лежит результат. Нам нужно найти число, которое при умножении на 56 даст 4424. Интуитивно попробуем число 80.

56*80=4480

Значит, искомое число меньше 80 и явно больше 70. Определим его последнюю цифру. Ее произведение на 6 должно заканчиваться цифрой 4. Согласно таблице умножения, нам подходят результаты 4 и 9. Логично предположить, что результатом деления может быть либо число 74, либо 79. Проверяем:

79*56=4424

Готово, решение найдено! Если бы не подошло число 79, второй вариант обязательно оказался бы верным.

Картина Н.П. Богданова-Бельского «Устный счёт. В народной школе С. А. Рачинского»

Полезные советы

В заключение приведем несколько полезных советов, которые помогут быстро научиться устному счету:

Польза устного счета неоспорима. Тренируйтесь, и с каждым днем вы будете считать все быстрее и быстрее. А если вам понадобится помощь в решении более сложных и многоуровневых задач, обращайтесь к специалистам студенческого сервиса за быстрой и квалифицированной помощью!

Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

Источник