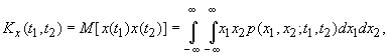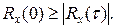характеристики и параметры случайных сигналов

Характеристики случайных измерительных сигналов

Свойства случайных сигналов оценивают с помощью статистических (вероятностных) характеристик. Они представляют собой неслучайные функции и (или) числа, зная которые, можно судить о закономерностях, которые присущи случайным сигналам, но проявляются только при их многократных наблюдениях.

Характеристики случайных сигналов, не изменяющихся во времени

Основными статистическими характеристиками сигнала, представленного случайной величиной (7.2), являются: функция распределения F_x(x), плотность распределения вероятностей р_х(х) (ПРВ), математическое ожидание т_ХУ дисперсия D_v среднеквадратическое отклонение (СКО) с_х и доверительный интервал Д_д. Рассмотрим эти характеристики.

1. Функция распределения (или интегральный закон распределения) F_x(x) выражает вероятность того, что конкретное значение случайной величины X окажется меньше, чем ее заданное значение х, т.е.

где Р(*) — символ вероятности события *.

2. Плотность распределения вероятностей (или дифференциальный закон распределения) ПРВ представляет собой функцию текущего значения случайной величины р_х(х)₉ выражающую вероятность попадания конкретного значения случайной величины X в малый интервал ее возможных значений Ах_у примыкающий к x_t т.е.

Размерность ПРВ р_х(х) обратна размерности величины х.

3. Математическое ожидание определяет средневзвешенное значение случайной величины X и вычисляется по формуле

Результат вычислений по этой формуле отличается от среднего значения случайной величины и совпадает с ним только в случае симметричных

законов распределения (равномерного, нормального и др.). о

Величинах = х-т_х называется центрированной случайной величиной. Математическое ожидание такой величины равно нулю.

4. Дисперсия случайной величины определяет средневзвешенное значение квадрата отклонения этой величины от ее математического ожидания. Дисперсия вычисляется по формуле

и имеет размерность, совпадающую с размерностью квадрата величины х.

5. Среднеквадратическое отклонение вычисляется по формуле

и, в отличие от дисперсии D_x, имеет размерность, совпадающую с размерностью измеряемой физической величины х. Поэтому СКО оказывается более удобным показателем степени разброса возможных значений случайной величины относительно ее математического ожидания.

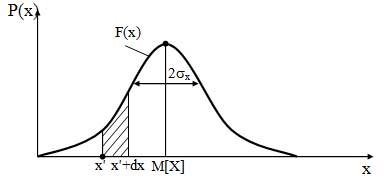
В соответствии с правилом «трех сигм» практически все значения случайной величины, обладающей нормальным законом распределения, попадают внутрь интервала х-т_х а площадь криволинейной трапеции с основанием [т_х ± Д_д] равна доверительной вероятности P_R (рис. 7.7). С ростом Рд доверительный интервал Д_д также увеличивается.

Рис. 7.7. К иллюстрации понятия «доверительный интервал»

Половину доверительного интервала Д_д можно определить, решая уравнение

В практике инженерных расчетов наиболее широкое применение среди перечисленных статистических характеристик случайного сигнала получила ПРВ р_х(х). Зная ПРВ, можно определить все другие статистические характеристики сигнала. Поэтому функция р_х(х) является полной статистической характеристикой случайного сигнала.

Перечислим основные свойства ПРВ.

1. р_х(х)>0, т.е. ПРВ — неотрицательная функция.

делить функцию распределения случайной величины F,.(x) и, наоборот, зная функцию распределения, можно определить ПРВ.

Источник

Характеристики случайных сигналов

Поскольку все информационные сигналы и помехи являются случайными и могут быть предсказаны лишь с некоторой степенью вероятности, то для описания таких сигналов используется теория вероятностей. При этом используются статистические характеристики, которые получают путем проведения многочисленных опытов в одинаковых условиях.

Все случайные явления, изучаемые теорией вероятностей можно разделить на три группы:
— случайные события;
— случайные величины;
— случайные процессы.

Случайное событие — это всякий факт, который в результате опыта может произойти или не произойти.
Случайным событием является появление помехи на входе приемника или прием сообщения с ошибкой.
Случайные события обозначаются латинскими буквами А, В, С.

Числовыми характеристиками случайного события являются:
1. Частота появления случайного события:

где m — количество опытов, в которых произошло данное событие;
N — общее количество проведенных опытов.

Как следует из выражения (40) частота появления случайного события не может превышать 1, т. к. количество опытов, в которых произошло данное событие не может привысить общее количество проведенных опытов.
2. Вероятность появления случайного события:

Т. е. вероятность появления случайного события есть частота его появления при неограниченном увеличении количества проведенных опытов. Вероятность появления события не может превышать 1. Случайное событие, имеющее вероятность равную единице является достоверным, т. е. оно обязательно произойдет, поэтому такую вероятность имеют уже произошедшие события.
Случайная величина — это величина, которая от опыта к опыту изменяется случайным образом.
Случайной величиной является амплитуда помехи на входе приемника или количество ошибок в принятом сообщении. Случайные величины обозначаются латинскими буквами X, Y, Z, а их значения — x, y, z.
Случайные величины бывают дискретными и непрерывными.
Дискретной называется случайная величина, которая может принимать конечное множество значений (например, количество оборудования, количество телеграмм и т. д., т. к. они могут принимать только целое число 1, 2, 3, …).
Непрерывной называется случайная величина, которая может принимать любые значения из некоторого диапазона (например, амплитуда помехи на входе приемника может принимать любые значения, точно так же как и любые значения может принимать информационный аналоговый сигнал).

Числовыми, статистическими характеристиками, описывающими случайные величины являются:
1. Функция распределения вероятности.

Данная характеристика показывает вероятность попадания значения случайной величины в малый интервал dx в окрестности точки х’, т. е. в заштрихованную область (рисунок).

3. Математическое ожидание.

где хi — значения случайной величины;
Р(хi) — вероятность появления этих значений;
n — количество возможных значений случайной величины.

где р(х) — плотность вероятности непрерывной случайной величины.

По своему смыслу математическое ожидание показывает среднее и наиболее вероятное значение случайной величины, т. е. это значение наиболее часто принимает случайная величина. Выражение (44) применяется, если случайная величина является дискретной, а выражение (45), если она является непрерывной. Обозначение M[X] является специальным для математического ожидания того случайной величины, которая указана в квадратных скобках, однако иногда используются обозначения mх или m.

4. Дисперсия.

Все характеристики случайной величины можно показать с помощью рисунка 22.

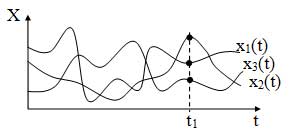
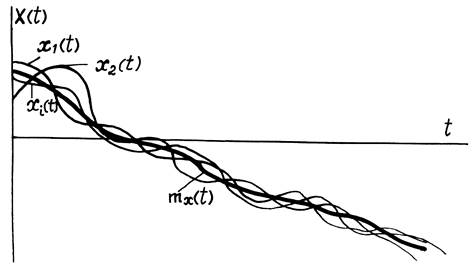
Случайный процесс — это такая функция времени t, значение которой при любом фиксированном значении времени является случайной величиной. Например, на рисунке 23 показана диаграмма некоторого случайного процесса, наблюдаемого в результате проведения трех опытов. Если определить значение функций в фиксированный момент времени t1, то полученные значения окажутся случайными величинами.

Таким образом, наблюдение любой случайной величины (Х) во времени, является случайным процессом Х(t). Например, как случайные процессы, рассматриваются информационные сигналы (телефонные, телеграфные, передачи данных, телевизионные) и шумы (узкополосные и широкополосные).
Однократное наблюдение случайного процесса называется реализацией xk(t). Совокупность всех возможных реализаций одного случайного процесса называется ансамблем реализаций. Например, на рисунке 23 представлен ансамбль реализаций случайного процесса, состоящий из трех реализаций.

Для характеристики случайных процессов используются те же характеристики, что и для случайных величин: функция распределения вероятности, плотность распределения вероятности, математическое ожидание и дисперсия. Данные характеристики рассчитываются аналогично, как и для случайных величин. Случайные процессы бывают различных типов. Однако в электросвязи большинство случайных сигналов и помех относятся к стационарным эргодическим случайным процессам.

Стационарным является случайный процесс, у которого характеристики F(x), P(x), M[X] и D[X] не зависят от времени.
Эргодическим является процесс, у которого усреднение по времени одной из реализации приводит к тем же результатам, что и статическое усреднение по всем реализациям. Физически это означает, что все реализации эргодического процесса похожи друг на друга, поэтому измерения и расчеты характеристик такого процесса можно проводить по одной (любой) из реализаций.
Кроме четырех характеристик приведенных выше случайные процессы также описываются функцией корреляции и спектральной плотностью мощности.

где tн — время наблюдения реализации xk(t).

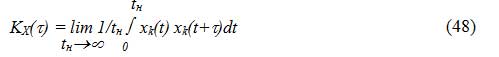
Спектральная плотность мощности — показывает распределение мощности случайного процесса по частотам.

Таким образом, наблюдение случайного явления во времени является случайным процессом, его появление является случайным событием, а его значение случайной величиной.

Например, наблюдение телеграфного сигнала на выходе линии связи в течение, какого то времени — это случайный процесс, появление на приеме его дискретного элемента «1» или «0» — случайное событие, а амплитуда этого элемента — случайная величина.

Источник

Вопрос 14 Параметры случайных сигналов

Наибольшее значение имеют следующие характеристики случайного

· математическое ожидание или первый начальный момент, равный

Математическое ожидание – это средняя функция, вокруг которой группируются реализации (см.рис. 1).

Многие параметры случайного процесса получают путем вычисления простейших функций от математического ожидания.

· дисперсия (разброс реализаций случайной величины относительно математического ожидания)

Корень квадратный от дисперсии называют среднеквадратическим отклонением (СКО):

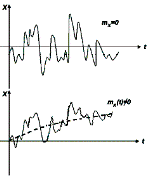
Если сечения случайного процесса описываются одним и тем же законом распределения, то математическое ожидание и дисперсия являются числами (параметрами). Если m_x=0, то говорят, что такой процесс имеет нулевое среднее; процесс x(t)- m_x (t) называется центрированным. Математическое ожидание называют первым моментом случайной величины, дисперсию – вторым центральным моментом.

Если для случайного процесса заданы двумерные плотности вероятно-

сти, что бывает необходимо при анализе быстроменяющихся процессов, то

определяют так называемую ковариационную функцию

которая определяет математическое ожидание произведений случайных функций в моменты t₁ и t₂. При t₁= t₂ имеем

т. е. при нулевом интервале между t₁, t₂ ковариационная функция определяет математическое ожидание от квадрата случайной величины. Разность между случайной величиной и её математическим ожиданием определяет флуктуации (изменения) сигнала. Для описания флуктуаций определяется автокорреляционная функция процесса

т.е. автокорреляционная функция в этом случае равна дисперсии. Часто при-

меняют нормированную корреляционную функцию

Источник

Модели и характеристики случайных сигналов

1. Особенности исследования САУ при случайных воздействиях

При детерминированных заранее заданных воздействиях состояние САУ в любой момент t определяется начальным состоянием системы в некоторый момент времени t0 и приложенными к системе воздействиями. Эта задача определяется решением соответствующего дифференциального уравнения

anx (n)+an-1x(n-1)+…+a0x=bmg(m)+bm-1g(m-1)+…+b0g. (26.1)

Однако в реальных условиях часто внешние воздействия изменяются случайно, т.е. заранее не предвиденным образом. Например:

суточные изменения нагрузки энергосистемы;

порывы ветра, действующие на самолет;

удары волны в гидродинамических системах;

сигналы радиолокационных установок;

шумы в радиотехнических устройствах и т.д.

Случайные воздействия могут прикладываться к системе извне (внешние воздействия) или возникать внутри некоторых ее элементов (внутренние шумы).

Конечно, можно задаться некоторыми максимальными значениями этих параметров и решить поставленную задачу (расчет системы на заданную точность при максимальных значениях случайных воздействий). Но поскольку максимальные значения случайной величины наблюдаются редко, то в этом случае к системе будут предъявлены заведомо более жесткие требования, чем это вызывается реальностью.

Правда, такой подход иногда является единственно возможным(высокоточное производство, иначе – брак). Поэтому в большинстве случаев расчет системы при случайных воздействиях ведут не по максимальному, а по наиболее вероятному значению случайных величин, т.е. по такому значению, которое встречается наиболее часто.

В этом случае получают наиболее рациональное техническое решение (меньший коэффициент усиления системы, меньшие габариты отдельных устройств, меньшее потребление энергии), хотя для маловероятных значений задающего воздействия будет иметь место ухудшение работы системы.

Расчет САУ при случайных воздействиях с помощью специальных статистических методов, которые оперируют статистическими характеристиками случайных воздействий, являющихся не случайными, а детерминированными величинами.

САУ, спроектированная на основе статистических методов, будет обеспечивать соответствующие требования не для одного, детерминированного воздействия, а для целой совокупности этих воздействий, заданных с помощью статистических характеристик (если ошибка САУ носит случайный характер, то точное ее значение в какой-либо момент времени при статистическом расчете получить невозможно).

Статистические методы расчета САУ основаны на расчетах и работах советских ученых: Хинчина А.Я., Колмогорова А.Н., Гнеденко В.В., Солодовникова В.В., Пугачева В.С., Казакова И.Е. и др., а также зарубежных ученых – Н. Винера, Л. Заде, Дж. Рагоцине, Калмана, Бьюси и др.

2. Краткие сведения о случайных процессах.

Случайной функцией называется функция, которая при каждом значении независимой переменной является случайной величиной. Слу­чайные функции, для которых независимой переменной является время t,называют случайными процессами. Так как в САУ процессы протекают во времени, то в дальнейшем будем рассматривать только случайные процессы.

Случайный процесс x(t) не есть определенная кривая, он явля­ется множеством определенных кривых x_i(t) (i=1,2,…,n), по­лучаемых в результате отдельных опытов (рис.26.1). Каждую кривую этого множества называют реализацией случайного процесса, и сказать, по какой из реализаций пойдет процесс, невозможно.

Рис. 26.1. Графики реализаций и математического ожидания случайного процесса

Функции F(x, t) и w(x, t) являются простейшими статис­тическими характеристиками случайного процесса. Они характеризуют случайный процесс изолированно в отдельных сечениях, не раскрывая связи между сечениями случайного процесса.

К основным характеристикам случайных процессов, наиболее ши­роко используемых при исследовании систем управления, относят: математическое ожидание, дисперсию, среднее значение квадрата слу­чайного процесса, корреляционную функцию, спектральную плотность и другие.

А. Математическое ожидание m_x(t) является средним значением случайного процесса x(t) по множеству и определяется

(26.2)

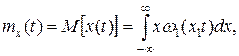
где w₁(x, t) — одномерная плотность вероятности случайного про­цесса x(t).

Математическое ожидание случайного процесса x(t) представляет собой некоторую неслучайную функцию времени m_x(t), около которой группируются и относительно которой колеблются все реализации дан­ного случайного процесса (рис. 26.1).

Средним значением квадрата случайного процесса называют вели­чину

(26.3)

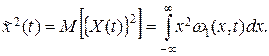
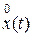
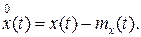
Часто вводят в рассмотрение центрированный случайный процесс , под которым понимают отклонение случайного процесса X(t) от его среднего значения m_x(t), или

(26.4)

Б. Дисперсия. Чтобы учесть степень разбросанности реализаций случайного про­цесса относительно его среднего значения, вводят понятие дисперсии случайного процесса, которая равна математическому ожиданию квад­рата центрированного случайного процесса

(26.5)

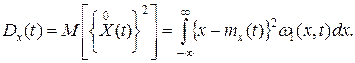
Дисперсия случайного процесса является неслучайной функцией времени D_x(t) и характеризует разброс случайного процесса Х(t) от­носительно его математического ожидания m_x(t).

На практике широко применяются статистические характеристики, имеющие ту же размерность, что и случайная величина, к которым от­носятся:

— среднее квадратическое значение случайного процесса

(26.6)

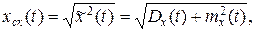
равное значению квадратного корня из среднего значения квадрата случайного процесса;

— среднее квадратичное отклонение случайного процесса

(26.7)

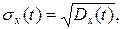
равное значению квадратного корня из дисперсии случайного процесса.

Математическое ожидание и дисперсия являются важными характе­ристиками случайного процесса, но не дают достаточного представления о внутренних связях случайного процесса, которые оказывают су­щественное влияние на характер его реализаций в пределах заданного интервала времени.

Одной из статистических характеристик, отражающих особенности внутренних связей случайного процесса, является корреляционная функция.

(26.8)

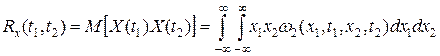
Случайные процессы в зависимости от того, как изменяются их статистические характеристики с течением времени, делят на стационарные и нестационарные. Различают стационарность в узком и широком смысле [15].

Стационарным в узком смысле называют случайный процесс Х(t), если его n-мерные функции распределения и плотность вероятнос­ти при любом n не зависят от положения отсчета времени t.

Стационарным в широком смысле называют случайный процесс X(t), математическое ожидание которого постоянно:

(26.10)

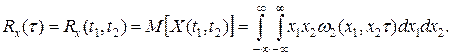
В теории случайных процессов пользуются двумя понятиями сред­них значений: среднее значение по множеству и среднее значение по времени.

Среднее значение по множеству определяется на основе наблюде­ния над множеством реализаций случайного процесса в один и тот же момент времени, т.е.

(26.11)

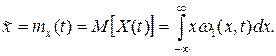
Среднее значение по времени определяется на основе наблюде­ний за отдельной реализацией случайного x(t) на протяжении доста­точно длительного времени Т, т.е.

(26.12)

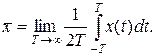
Из эргодической теоремы вытекает, что для так называемых эргодических стационарных случайных процессов среднее значение по множеству совпадает со средним значением по времени, т.е.

(26.13)

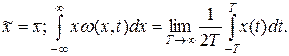
В соответствии с эргодической теоремой для стационарного слу­чайного процесса с математическим ожиданием m_0x=0 корреляционную функцию можно определить

(26.14)

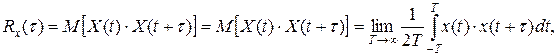
Статистические свойства связи двух случайных процессов Х(t) и G(t) можно характеризовать взаимной корреляционной функцией R_xg(t₁,t₂), которая для каждой пары произвольно выбранных значении аргументов t₁ и t₂ равна

(26.15)

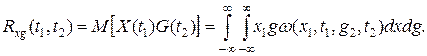
Согласно эргодической теореме вместо (26.15) можно записать

(26.16)

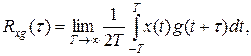
где x(t) и g(t)- любые реализации стационарных случайных процес­сов Х(t) и G(t).

Если случайные процессы Х(t) и G(t) статистически не связаны друг с другом и имеют равные нулю средние значения, то их взаимная корреляционная функция для всех t равна нулю.

Приведем некоторые свойства корреляционных функций.

1. Начальное значение корреляционной функции равно среднему

значению квадрата случайного процесса:

(26.17)

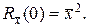
2. Значение корреляционной функции при любом t не может превышать ее начального значения, то есть

3. Корреляционная функция есть четная функция от t, т.е.

(26.18)

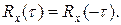
Другой статистической характеристикой, отражающей внутреннюю структуру стационарного случайного процесса Х(t), является спект­ральная плотность S_x(w), которая характеризует распределение энергии случайного сигнала по спектру частот.

Г. Спектральная плотность S_x(w) случайного процесса Х(t) опре­деляется как преобразование Фурье корреляционной функции R(t),

(26.19)

(26.20)

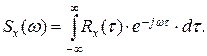
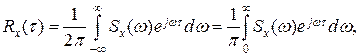
так как спектральная плотность S_x(a) является действительной и четной функцией частоты w.

Соотношения (26.19) и (26.20) позволяют установить некоторые зависимости между структурой случайного процесса Х(t) и видом ха­рактеристик R_x(t) и S_x(w) (рис.26.2).

Ид приведенных графиков следует, что с увеличением скорости изменения реализации Х(t) корреляционная функция R_x(t) сужает­ся (обостряется), а спектральная плотность S_x(w) расширяется.

Дата добавления: 2015-12-11 ; просмотров: 1117 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник