какие изображения применяются для получения наглядного изображения предметов пространства

86. Построение наглядного изображения предмета

Для построения наглядного изображения предмета воспользуемся аксонометрическими проекциями (гл. 12). Выполнить его можно по его комплексному чертежу. Воспользовавшись рис. 172, построим

стандартную прямоугольную изометрию изображенного на нем предмета. Воспользуемся приведенными коэффициентами искажения. Примем расположение начала координат (точка О) — в центре нижнего основания предмета (рис. 198). Вычертив оси изометрии и установив масштаб изображения (М А 1,22 : 1), отмечаем центры окружностей верхнего и нижнего оснований цилиндра, а также окружностей, ограничивающих Т-образный вырез. Вычерчиваем эллипсы, являющиеся изометрией окружностей (см. § 77). Затем проводим линии, параллельные координатным осям, которые ограничивают вырез в цилиндре. Изометрию линии пересечения сквозного цилиндрического отверстия, ось которого

параллельна оси Оу с поверхностью основного цилиндра, строим по отдельным точкам, используя те же точки (К, L, М и им симметричные), что и при построении вида слева. Затем удаляем вспомогательные линии и обводим окончательно изображение с учетом видимости отдельных частей предмета.

Плоские фигуры, получаемые при этом, уже построены на комплексном чертеже, так как они являются половинами фронтального и профильного разреза предметов (рис. 185, б).

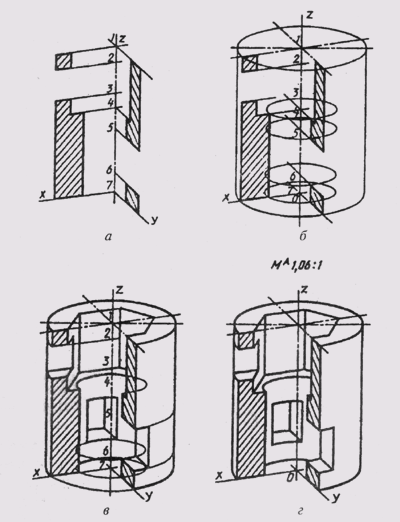
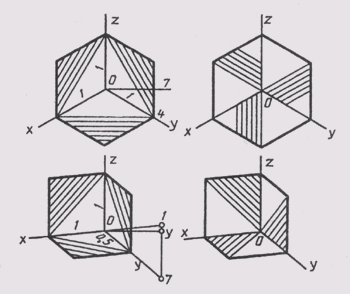
Построение наглядного изображения начинаем с проведения осей диметрии и указания масштаба М А 1,06 : 1 (см. § 78). На оси z отмечаем положение центров 1, 2. 7 (рис. 199, а); расстояния между ними берем с главного вида предмета. Через отмеченные точки проводим оси диметрии. Затем строим в диметрии фигуры сечения сначала в плоскости xOz, а затем в плоскости yOz. Размеры координатных отрезков берем с комплексного чертежа (рис. 185); при этом размеры по оси у сокращаем в два раза. Выполняем штриховку сечений. Угол наклона линий штриховки в аксонометрии определяется диагоналями параллелограммов, построенных на аксонометрических осях с учетом коэффициентов искажения. На рис. 200, а приведен пример выбора направления штриховки в изометрии, а на рис. 200, б — в диметрии. Далее строим эллипсы — диметрию окружностей, расположенных в горизонтальных плоскостях (см. рис. 199, б). Проводим контурные линии наружного цилиндра, внутренних вертикальных отверстий, строим основание этих отверстий (рис. 199, в); вычерчиваем видимые линии пересечения горизонтальных отверстий с наружной и внутренними поверхностями.

Затем удаляем вспомогательные линии построения, проверяем правильность выполнения чертежа и обводим чертеж линиями требуемой толщины (рис. 199, г).

Источник

Какие изображения применяются для получения наглядного изображения предметов пространства

При построении комплексного чертежа изображаемый предмет обычно располагают так, чтобы направления трех главных измерений (длина — высота — ширина — были бы параллельны координатным осям плоскостей проекций (рис. 2.31, а). Обычно . В этом случае на каждой из проекций два измерения проецируются в натуральную величину без искажения, но третье измерение проецируется в точку, т. е. отсутствует. Поэтому для полного представления о форме предмета необходимы еще одна или несколько проекций на другие плоскости проекций. Несколькими проекциями можно добиться полной информативности комплексного чертежа о форме предмета. Однако на таком чертеже теряется одно из основных качеств изображения, а именно наглядность. Представить истинную пространственную форму предмета по такому чертежу бывает достаточно трудно, особенно для предметов сложной геометрической формы.

Для того чтобы чертеж стал наглядным, необходимо построить проекцию предмета, на которой ни одно из главных измерений не проецировалось бы в точку. Для этого предмет следует соответствующим образом расположить перед плоскостями проекций, чтобы он был виден сразу с трех сторон: спереди, сверху и слева (рис. 2.31, б).

Наглядные изображения могут быть выполнены в свободной манере с приближенным соблюдением соотношений размеров по осям, а могут быть построены по определенным законам. В наглядных изображениях искажаются углы между координатными осями (рис. 2.31, е) и линейные размеры по этим осям. Отношение длины проекции отрезка, параллельного координатной оси, к его истинной длине определяет коэффициент искажения размера по этой оси: — коэффициент искажения вдоль оси х; — то же вдоль оси то же вдоль оси Наглядные изображения, построенные с заданными коэффициентами искажения по главным измерениям и углами между координатными осями, называют аксонометрическими роекциями.

Для прямоугольных аксонометрических проекций существует зависимость между коэффициентами искажения

Правила построения стандартных аксонометрических проекций устанавливает ГОСТ 2.317-69. Наибольшее применение на практике имеют следующие аксонометрические проекции: изометрическая и днметрическая прямоугольные проекции, косоугольная фронтальная диметрическая проекция (рис. 2.32).

Рис. 2.31. Построение наглядного изображения. а — комплексный чертеж; наглядное изображение; в — расположение координатных осей

Изометрическая прямоугольная проекция предполагает, что коэффициенты искажения по всем трем осям одинаковы:

и в соответствии с вышепрннятой формулой равны 0,82. Углы между координатными осями также одинаковы, и равны (рис. 2.33,а). Как правило, при построении изображения предмета в изометрической проекции в целях упрощения используют приведенный коэффициент искажения -Изображение в этом случае получается несколько увеличенным, как бы построенным в масштабе

Диметрическая прямоугольная проекция предполагает одинаковыми коэффициенты искажения по двум осям. В стандартной форме диметрической прямоугольной проекции приняты одинаковыми коэффициенты искажения по осям и 2, а по оси у — в 2 раза меньший, т.е. Действительные коэффициенты искажения равны В целях упрощения построения диметрическую проекцию выполняют без искажения по осям и с коэффициентом искажения по оси Положение координатных осей для днметрической прямоугольной проекции приведено на рис.

Косоугольная фронтальная диметрическая проекция имеет те же коэффициенты искажения, что и прямоугольная диметрическая проекция, но выгодно отличается от нее более удобным расположением координатных осей, что упрощает геометрические построения.

Из других косоугольных аксонометрических проекций, которые рекомендует следует назвать изометрические фронтальную и горизонтальную проекции, каждая из которых выполняется без искажения по всем трем осям: (Подробнее об этих проекциях см.

Необходимо остановиться на построении проекций окружностей в аксонометрии. Как правило, проекциями окружностей являются эллипсы (рис. 2.34). Исключение составляет косоугольная фронтальная диметрическая проекция окружности, лежащей в плоскости, параллельной фронтальной плоскости. Эта проекция представляет собой заданную окружность без искажений. Параметры эллипсов, представляющих собой проекции окружностей, лежащих в координатных плоскостях, приведены

Рис. 2.33. Положение аксонометрических осей: а — изометрии; днметрии; в — косоугольная фронтальная диметрня

Рис. 2.34. Аксонометрические проекции окружностей

в табл. 2.3. Следует заметить, что размеры диаметров эллипсов, параллельных координатным осям, равны диаметрам заданных окружностей.

Чаще всего аксонометрические проекции применяются для построения наглядных изображений деталей. Но возможны случаи, когда в целях усиления наглядности изображение сборочной единицы строится в аксонометрической проекции (рис. 2.35).

Для показа внутренних форм предмета в аксонометрических проекциях используют разрезы. Чаще всего плоскости разреза совпадают с главными плоскостями симметрии (рис. 2.35). В аксонометрических проекциях, как правило, не применяют полных разрезов, не пользуются теми условностями, которые применяют в комплексных чертежах. Линии штриховки сечений наносят параллельно диагоналям квадратов, лежащих в соответствующих плоскостях проекций. При нанесении размеров выносные линии проводят параллельно аксонометрическим осям, размерные линии — параллельно измеряемому отрезку.

Аксонометрические изображения являются самыми простыми из наглядных изображений, применяемых в технике, и используются достаточно широко. Но метод параллельного проецирования, который используется при построении аксонометрических проекций, не позволяет строить изображения предметов такими, как мы их видим в действительности. Метод параллельного проецирования не учитывает следующие основные законы зрения человека:

1) равные между собой расстояния при удалении от наблюдателя, кажутся уменьшающимися;

2) параллельные линии сходятся в одной точке.

Построить изображение предметов с учетом этих зрительных законов можно, использовав метод центрального проецирования, при котором все проецирующие прямые

Таблица 2.3. (см. скан) Окружности в аксонометрических проекциях

Рис. 2.35. (см. скан) Разрезы в аксонометрии

пересекаются в одной точке, называемой центром проецирования.

Сущность метода центрального проецирования представлена на рис. 2.36. Проецирующие прямые выходят из центра проецирования Изображение предмета строится на плоскости К, которая носит название картинной плоскости. Изображение предмета, построенное по методу центрального проецирования с учетом отмеченных выше законов зрения, носит название перспективного изображения, или, просто, перспективы. Часто перспективой называют метод построения изображений на картинной плоскости в соответствии с теми кажущимися сокращениями размеров и изменениями очертаний формы, которые наблюдаются в действительности.

Чтобы построить перспективу предмета, необходимо иметь две его проекции (рис. 2.37, а,б). На горизонтальной проекции (рис. 2.37,б) выбирается положение центра

Рис. 2.36. Метод центрального проецирования

проецирования и положение картинной плоскости К. Наиболее выразительным и естественным перспективное изображение бывает, если угол зрения а выбирается в пределах На фронтальной проекции (рис. 2.37,а) намечается высота линии горизонта Из центра проецирования проводим через характерные точки горизонтальной проекции проецирующие прямые и определяем проекции этих характерных точек на картинной плоскости. Далее находим точки схода параллельных прямых поперечного и продольного направлений, проводя из точки прямые, параллельные соответствующим сторонам предмета на горизонтальной проекции. Полученные точки используются при построении перспективы предмета (рис. 2.37, в). От положения картинной плоскости и линии горизонта зависит видимая форма предмета.

Сравнение различных изображений однбго и гого же предмета комплексного чертежа (см. рис. 2.21, 2.25), аксонометрических проекций (см. рис. 2.32) и перспективы (рис. 2.37) говорит о преимуществах и недостатках того или иного изображения. Комплексный чертеж дает полную информацию о форме и размерах предмета, однако изображение не является наглядным. Перспективное изображение является наиболее натуральным из всех видов изображений, но размеры предмета на

Рис. 2.38. (см. скан) Перспектива тепловой электростанции

Рис. 2.39. (см. скан) Перспектива здания приборостроительного завода

чертеже являются искаженными. Аксонометрические наглядные изображения являются более простыми для построения, чем перспективные изображения.

Наиболее широко перспектива используется в строительных и архитектурных чертежах, где изображаемые предметы имеют значительную протяженность в пространстве и изображение зданнй и сооружений на чертежах должно соответствовать восприятию их глазом человека.

Иллюстративный материал архитектурно-строительной документации включает в себя чертежи, в которых изображения, построенные в линейной графике, дополняются передачей светотени, фактуры материалов здания (рис. 2.38, 2.39). Для усиления

Рис. 2.40. (см. скан) Перспектива здания научно-исследовательского института

реальности изображения здания дополняются окружающими их предметами: соседней застройкой, растительностью, людьми и т. д. (рис. 2.40).

Источник

Лекция 5. ИЗОБРАЖЕНИЕ ПРЕДМЕТОВ И ПРОСТРАНСТВА

Последовательность изображения предметов.

Процесс изображения предметов состоит из четырех этапов: схематизации, типизации, индивидуализации и обобщения.

5.1.1.Схематизация

На первом этапе изображения намечают предметную форму в упрощенном виде, немногими линиями и абстрактными обобщенными фигурами. Такой рисунок представляет собой схему, мало понятную непосвященному, но необходимую для рисующего, так как создавая ее, он начинает строить композицию, намечает основные пропорции и части предмета, их положение и движение всей массы формы. Эта схематизация предполагает детальное изучение предмета и является предпосылкой правильного решения задач следующего этапа изображения.

Изучение предмета всегда начинают с постановки и выяснения вопросов конструкции: что это такое? Зачем этот предмет нужен? Из каких частей он состоит? Зачем нужны эти части? Что они несут? Как соединяются друг с другом?

Для изображения конструктивных особенностей предмета выявляют его положение; основные размеры; направление движения формы; место на листе бумаги, которое займет предмет; величину рисунка. Последовательное выяснение этих вопросов помогает решению композиционной задачи рисунка.

Изображение конструктивных элементов и пространственной формы требует выделения основных несущих и несомых частей предмета, а также наблюдения контуров, ограничивающих эти части: какой линией или фигурой можно изобразить основные части? Как расположить эту фигуру на листе относительно его горизонтальных и вертикальных краев? Каково направление контуров основных частей предмета? Какими линиями надо изображать верхние (нижние, левые и правые) части контура?

5.1.2.Типизация

Типизация представляет собой второй этап рисования, позволяющий обогатить схематическое изображение более конкретными признаками, которые выявляют типичные особенности данного предмета, свойственные целой группе родственных предметов.

Для выделения типичных признаков предмета внимательно рассматривают его основные конструктивные части, определяют их размеры, характер контуров и их соединений друг с другом.

5.1.3.Индивидуализация

Каждый предмет обладает наряду с типичными индивидуальными признаками и определенными качествами. Они закладываются природой и человеком, создающим предмет или пользующимся им. Эти признаки, придавая неповторимое своеобразие данному предмету, способны не только отличить его от других, но и поведать о его происхождении, какое отношение имели люди к этой вещи, а также кто эти люди.

Внимательное изучение модели помогает выявить: есть ли второстепенные части у модели? Как они называются? Зачем нужны? Где находятся? Каковы их положения и размеры? Какими линиями их можно изобразить?

Когда линейный рисунок закончен, стирают все вспомогательные линии и штрихи и переходят к передаче светлоты, фактуры, освещенности и, если надо, цвета.

Обобщение

Объект изображения требует анализа, то есть мысленного дробления предмета на составляющие его части, отрыва одного признака или свойства от других. Целостное изображение натуры достигается при умении одновременно видеть части и предмет в их нерасторжимом единстве. Такое цельное видение позволяет обобщить детально разработанную, часто дробную и несогласованную в частях форму, то есть подчинить части и второстепенное главному, установить пропорциональные отношения между одноименными признаками, существующими в натуре. Четвертый этап последовательного изображения предмета завершается обобщением того, что было сделано в предшествующий период. Для этого рисующий садится прямо, ставит фронтально на вытянутую руку рисунок и сравнивает нарисованное с моделью, стараясь не видеть отдельных деталей в натуре и в ее изображении. Если в процессе сравнения возникает ощущение дробности рисунка, значит, нарушены существенные связи между целым и деталями.

Изображение предметов

Изображение предметов – это результат выявления основных связей между рисующим, предметом и средой. Объемный предмет представляет собой единое целое, отделенное от пространства поверхностями, ребрами и вершинами, то есть элементами, обладающими определенными признаками и свойствами. Среду образуют предметная плоскость и фон. Предметная плоскость – это горизонтальная поверхность, на которой располагается рисуемый нами предмет. Фон выступает в качестве экрана. При рисовании объемного предмета надо представлять себе фон как глубину, как пространственную среду, в которой располагается наш предмет.

Для рисования нужен образ, сформированный в одном положении. Это одно наиболее выгодное положение закрепляется зрительной позицией или точкой зрения рисующего. Выбранная точка зрения определяет положение предмета и рисующего, устанавливает практическую связь между ними, а через линию горизонта – связь и с картинной плоскостью.

Линия горизонта необходима в рисунке в момент его построения, помогает правильно найти место изображаемых предметов на картинной плоскости, реалистически убедительно нарисовать их со всеми перспективными изменениями согласно законам перспективы. Линия горизонта всегда находится на уровне глаз рисующего и возникает в месте пересечения мысленно поставленной перед глазами, бесконечно длинной горизонтальной плоскости с картинной плоскостью.

Наука, излагающая законы, которые помогают изображать предметы так, как их воспринимает наш глаз, называется перспективой. Перспективу делят на линейную и воздушную. Перспективные изменения пространственной формы, размеров, направлений контуров, то есть тех признаков, которые можно изобразить линией, относят к линейной перспективе. Перспективные изменения физических признаков – светлоты, цвета, фактуры, которые передаются тоном и цветом, относят к воздушной перспективе.

Сформулируем основные правила линейной перспективы:

1. Для изображения глубины дальний предмет следует частично закрывать ближним.

2. Ближний предмет следует изображать крупнее удаленного.

3. Основание ближнего предмета следует изображать ниже основания удаленного.

4. Горизонтальные ребра, параллельные картинной плоскости, надо изображать прямыми горизонтальными линиями.

5. Горизонтальные ребра в угловом положении надо изображать наклонными линиями.

6. Горизонтальные ребра в угловом положении надо изображать короче, чем во фронтальном положении.

7. Вертикальные в натуре ребра надо изображать вертикальными линиями.

8. Плоскость во фронтальном положении надо изображать без перспективных изменений, а в угловом – изображать, сокращая ее и изменяя направление горизонтальных ребер, уходящих в глубину.

9. Горизонтальную плоскость, расположенную далеко от линии горизонта, надо изображать менее сокращенной, чем плоскость, расположенную близко, а плоскость, находящуюся на линии горизонта, – горизонтальной линией.

10. Плоскость круглой формы во фронтальном положении надо изображать окружностью, а в угловом – эллиптической фигурой.

Изображение пространства

Чтобы правдиво передать особенности видимого пространства на рисунке, необходимо знать и уметь применять законы воздушной перспективы. Воздушной перспективой называются кажущиеся изменения некоторых признаков предметов под воздействием воздушной среды и пространства. Перечислим основные законы воздушной перспективы:

1. Все ближние предметы воспринимаются подробно, а удаленные – обобщенно; для передачи пространства ближние предметы надо изображать детально, а дальние – обобщенно.

2. Все ближние предметы воспринимаются четко, а удаленные – неопределенно; для передачи пространства контуры ближних предметов надо делать резче, а удаленных – мягче.

3. На большом расстоянии светлые предметы кажутся темнее, а темные – светлее ближних; для передачи пространства удаленные светлые предметы надо слегка притенять, а темные – осветлять.

4. Все ближние предметы обладают контрастной светотенью и кажутся объемными, все дальние – слабо выраженной светотенью и кажутся плоскими; для передачи пространства ближние предметы надо изображать объемно, а дальние – плоско.

5. Все удаленные предметы, прикрываясь воздушной дымкой, приобретают цвет этой дымки – фиолетовый, синий, голубой или беловатый; для изображения пространства надо ближние предметы изображать яркоокрашенными, а удаленные – бледными.

6. Все ближние предметы кажутся многоцветными, а удаленные – одноцветными; для передачи пространства ближние предметы надо изображать различными по цвету красками, а удаленные – одинаковыми.

Лекция 6. Ц В Е Т

Цвет окружает нас повсюду. Он такой же естественный компонент нашей жизни, как воздух, которым мы дышим. И все же в отдельные моменты, обратив внимание на какое-нибудь поразившее нас необычное цветовое сочетание, мы удивляемся и задаем себе вопрос – что же, собственно, представляет собой цвет?

Наукой доказано, что цветовое зрение отличает человека от большинства представителей животного мира. И поскольку зрение выполняет функции одного из основных каналов восприятия информации о внешнем мире, то именно цвет играет наиболее важную роль в процессе ее интерпретации.

Воздействие цвета на человека многогранно. В повседневной жизни он определяет наше настроение и самочувствие, оказывает влияние на работоспособность и психологическое состояние. Не существует, пожалуй, ни одной сферы деятельности человека, ни одной профессии, где бы не приходилось решать вопросы, связанные с цветом.

Поэтому понимание того, что на самом деле представляют собой цвет, психология его восприятия и механизмы воздействия на цветовые рецепторы нашего глаза очень важно для правильного применения его на практике.

Цветовой тон – это оттенок, характеризующий цвет как красный, синий и т.д. Это главный признак, отличающий хроматические цвета.

Насыщенность – это степень выраженности цветового тона. Насыщенными называют цвета цветового круга, малонасыщенными – осветленные или затемненные. Насыщенные цвета получают растворением в воде такого количества акварельной краски, которое не дает ни осветленных, ни затемненных цветов и наилучшим образом выявляет цветовой тон данного цвета. Малонасыщенный осветленный цвет получают растворением небольшого количества акварельной краски в большом количестве воды; добавлением белил в гуашевую краску; ослаблением нажима на цветной карандаш. Малонасыщенный затемненный цвет получают соединением данного цвета с другими темными цветами, и в первую очередь, с черным цветом.

Светлота – это признак, определяющий цвет как светлый или темный. В цветовом круге наибольшей светлотой обладает желтый цвет, а наименьшей – фиолетовый.

Ахроматическими называют белые, серые и черные цвета (некрасочные). Они обладают только светлотой.

Для получения других цветов и различных оттенков пользуются приемом, называемым смешением. Наиболее частыми видами смешения в практике являются слагательное и вычитательное.

Вычитательное смешение основано на создании одного или нескольких красочных слоев, через которые проходят все лучи белого светового потока; при этом цветные лучи преломляются, поглощаются и отражаются, а в глаз попадают лишь те лучи, которые были вычтены красочным слоем из всего светового потока. Вычитательное смешение выполняют двумя способами: лессировкой и алла прима. Лессировка – это прием живописной техники, позволяющий получить нужные цвета и оттенки наложением одного прозрачного красочного слоя на другой. Алла прима – это прием получения цвета механическим смешением красок на палитре или вливанием одной красочной смеси в другую.

Слагательное смешение основано на особенностях нашего зрительного восприятия. Человек на определенном отдалении многоцветную поверхность видит одноцветной. Разные цвета как бы сливаются в один цвет. Сложение цветов происходит на расстоянии, поэтому слагательное смешение иногда называют пространственным.

Три краски – красную, синюю и желтую – называют основными: смешивая их, получают многие другие цвета. Цвета, полученные от смешения нескольких разноцветных красок, называют производными или сложными.

Цветовой круг можно разделить на две части: теплую и холодную. Теплыми цветами будут: красные, оранжевые, желтые, желто-зеленые цвета (цвета огня и солнца). Холодными будут сине-зеленые, синие и фиолетовые цвета (цвета льда и луны).

В рисовании приходится уделять внимание вопросам восприятия цвета. Объективные свойства цвета сохраняются, но один и тот же цвет, помещенный в различную цветовую среду, будет восприниматься несколько различно.

Контраст светлотный. В тех случаях, когда в зависимости от других цветов изменяется светлота цвета, контраст называется светлотным. Под влиянием цвета, окружающего цветовое пятно, может изменяться светлота пятна независимо от того, являются ли фон и наблюдаемый на нем цвет хроматическими или ахроматическими. Так, цвет, окруженный белым фоном, кажется значительно темнее такого же цвета, помещенного на черный фон.

Контраст хроматический. Изменение цветового тона или насыщенности цвета в зависимости от окружающих его других цветов носит название хроматического контраста. Всякий цвет в окружении других цветов будет восприниматься несколько иным: или приобретая цветной оттенок, или меняя свой цветовой тон, или изменяясь по насыщенности. Так, серый цвет, помещенный на синий фон, кажется желтоватым, на красном фоне – зеленоватым, на зеленом – с розоватым оттенком.

Одновременный контраст цветов. Когда одновременно изменяются и светлота, и цветовой тон в зависимости от соседнего цвета. Это явление носит название одновременного контраста.

Краевой контраст. Если взять несколько прямоугольников и покрыть каждый из них ровным серым цветом, причем каждый следующий прямоугольник делать несколько светлее предыдущего, то каждый из них будет восприниматься как бы закрашенным не ровным тоном, а с убывающей темнотой.

Источник