какие задачи относятся к позиционным
1. Глава 10. Позиционные задачи
§ 60. Общие сведения о позиционных задачах
Задачи, связанные с решением вопросов взаимного расположения геометрических фигур на комплексном чертеже, называются позиционными.
Среди позиционных можно выделить две группы задач, представляющих наибольший практический интерес. К ним относятся задачи на взаимную принадлежность и задачи на взаимное перенесение. Задачи первой группы неоднократно упоминались при изучении глав 7 и 8. Это объясняется, тем, что любая линия есть производная точки, а любая поверхность есть производная линии. Конкретно вопросы принадлежности точки прямой рассмотрены в § 44, принадлежности точки и прямой плоскости в § 49, а принадлежности точки и линии поверхности в § 55.
Решение позиционных задач на принадлежность предполагает работу с линиями поверхности графически простыми, например прямой или окружностью. Это необходимо для того, чтобы не усложнять построений на комплексном чертеже. Для правильного выбора этих линий надо знать, какие семейства линий несет на себе та или иная поверхность.
Задачи на взаимное пересечение связаны с построением точек, принадлежащих одновременно двум рассматриваемым геометрическим образам, например прямой и плоскости, двум плоскостям, плоскости и поверхности, двум поверхностям. Каждую из этих точек строят в пересечении двух вспомогательных линий. Эти линии должны быть графически простыми и принадлежать одной вспомогательной плоскости или поверхности. Выбор вспомогательных, поверхностей (посредников), несущих в себе вспомогательные линии, зависит от формы пересекающихся поверхностей. Совокупность построенных общих точек позволяет построить линию пересечения геометрических образов.
Позиционные задачи



При параллельном проецировании между оригиналом и его проекциями сохраняются некоторые свойства, которые называются проективными, или инвариантными (независимыми для данного способа проецирования).
Базируясь на инвариантных свойствах параллельного проецирования, можно доказать любую теорему или воспроизвести оригинал по заданным проекциям. Можно утверждать, что в начертательной геометрии существует как бы две системы аксиом. Одна – используется в процессе построения проекции геометрической фигуры по ее оригиналу, и на этом этапе действия аксиом выполняют инвариантные свойства параллельного проецирования. После того, как проекции определены, вступает в силу другая система – аксиоматика евклидовой геометрии.
Рассмотрим третий инвариант параллельного проецирования, на основании которого решается группа задач, называемых позиционными.
Если в пространстве точка принадлежит линии, то проекция этой точки принадлежит проекции линии:
Позиционные задачи, в которых рассматривается вопрос о взаимной принадлежности заданных геометрических фигур. Все многообразие позиционных задач можно отнести к трем группам:
1) задачи на построение линий пересечения двух поверхностей;
2) задачи на определение точек пересечения линий с поверхностью;
3) задачи на принадлежность точки поверхности.
Алгоритм для решения задачи построения
линии пересечения поверхностей
При решении задачи на построение точки, принадлежащей линии, достаточно воспользоваться этим свойством.
Если точка А Î линии С, то ортогональная проекция A1 Î С1 и А2 Î С2.
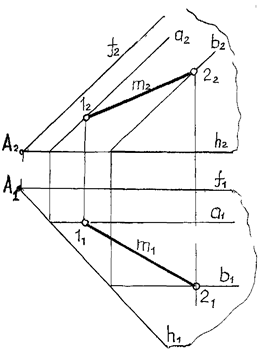
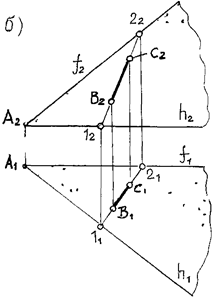
Пример: Указать горизонтальную проекцию точки С по данной ее фронтальной проекции, если известно, что С Î [АВ] (рис. 19):
А Î l Þ (А1 Î l1) Ù (A2 Î 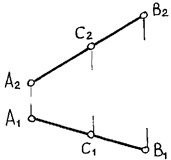
Рис. 19. Точка С принадлежит прямой
Принадлежность точки поверхности А Î a
Воспользуемся тем же свойством (1) для того, чтобы на чертеже поверхности указать проекции принадлежащей ей точки. Вначале необходимо построить проекции какой-либо линии, принадлежащей поверхности, а затем на этой линии отметить точку.
Пример: В плоскости a (a çêb) указать произвольную точку А.
1. Проводим h Î a (а çêb).
Рис. 20. Точки 1 и 2 принадлежат плоскости
Принадлежность линии поверхности (l Î a)
Пример: Построить фронтальную проекцию прямой l, принадлежащей плоскости D АBС, если известна ее горизонтальная проекция l1.
Построение линии, принадлежащей поверхности, принципиально не отличается от построения точки, принадлежащей поверхности. Различие лишь в том, что определяется проекция не одной, а n точек, принадлежащих линии.
При построении прямой, принадлежащей плоскости, достаточно определить проекции двух точек, на прямой.
Рис. 21. Принадлежность линии поверхности l Î a плоскости D АВС
Как определить точки пересечения линий на комплексном чертеже? Вытекает из свойства (2):
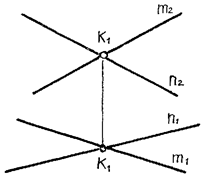
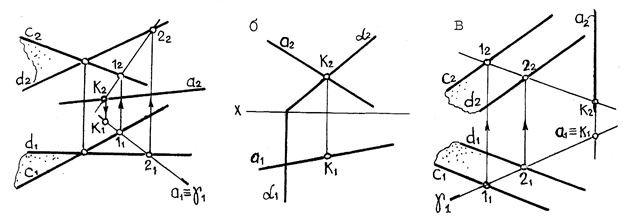
Пример: Показать на эпюре Монжа две пересекающиеся прямые m и n.
тогда к Î m и (1) K Î n (2).
т.е. одноименные проекции прямых пере-
секающихся и проекции точки пересече-
ния лежат на одной линии связи.
Рис. 22. Две пересекающиеся прямые m и n
Пересечение поверхности с поверхностью (a и b)
Две поверхности пересекаются по линии, точки которой принадлежат каждой из пересекающихся поверхностей.
Поэтому нахождение линии пересечения двух поверхностей сводится к нахождению общих точек, принадлежащих как множеству точек, составляющих поверхность a, так и множеству точек, входящих в состав поверхности b.
Способ построения линии пересечения двух поверхностей состоит в следующем:
| Словесное описание на языке начертательной геометрии: | Символическая запись на языке геометрии: |
| 1. Вводим вспомогательные секущие плоскости gi. 2. Определяем линии пересечения этой вспомогательной плоскости с каждой из заданных поверхностей. 3. Находим точки, в которых пересекаются полученные линии пересечения. Соединяем эти точки плавной линией. | Вводим gi. Определяем: mj = gi Ç a, nj = gi Ç b. Находим: Lj = mj Ç n, l = L1 È L2 È L3 … Ln. |
Алгоритм нахождения точек, общих для двух заданных множеств точек-поверхностей a и b, можно записать в виде
где gi – поверхность конуса; b – поверхность сферы.
Чтобы построить линию пересечения поверхностей на чертеже, следует найти точки, общие для обеих поверхностей, с помощью конкурирующих простых графических линий. Для данных поверхностей такими линиями являются окружности (pиc. 25).
В алгоритме для решения задач по определению линии пересечения двух поверхностей a и b в качестве вспомогательной поверхности (посредника) следует выбирать поверхности, которые пересекали бы заданные поверхности a и b по наиболее простым для построения линиям – прямым и окружностям. Поэтому в качестве посредников принимают плоскости или сферы. В связи с этим можно говорить о различных вариантах решения задач по определению линии пересечения поверхностей.
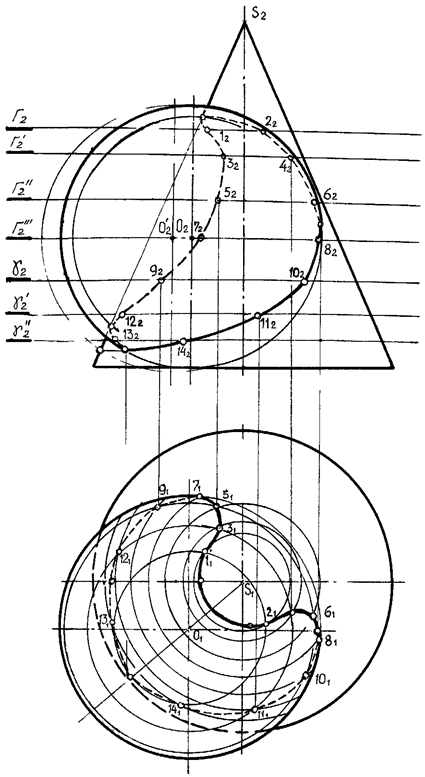
Рис. 23. Построение точек линии пересечения конуса и сферы способом секущих плоскостей Г2, Г’2, Г»2, … g2, g’2, g»2
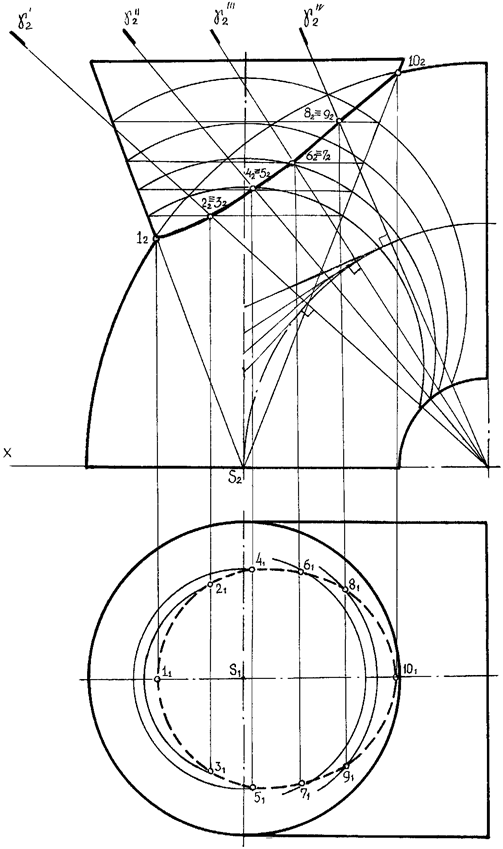
Рис. 24. Построение точек линии пересечения двух конических поверхностей способом концентрических сфер g2g’2 = g»2
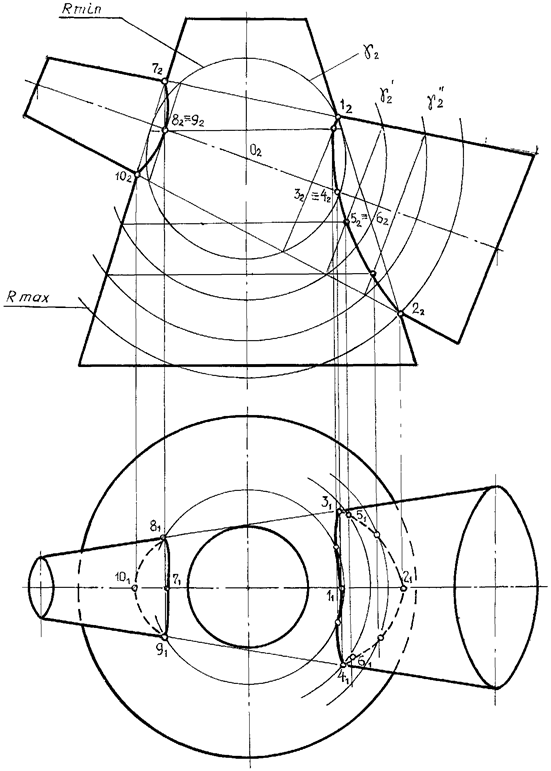
Рис. 25. Построение точек линии пересечения открытого тора
и конуса способом эксцентрических сфер
Существует два варианта использования вспомогательных секущих плоскостей (рис. 22):
1) плоскости общего положения,
2) плоскости проецирующие.
Существует также два варианта использования сферических поверхностей (рис. 24, 25):
1) концентрических сфер – используется семейство сфер различных радиусов, проведенных из одного центра;
2) эксцентрических сфер – радиусы сфер могут быть как одинаковыми, так и различными, проведенными из разных центров (рис. 25).
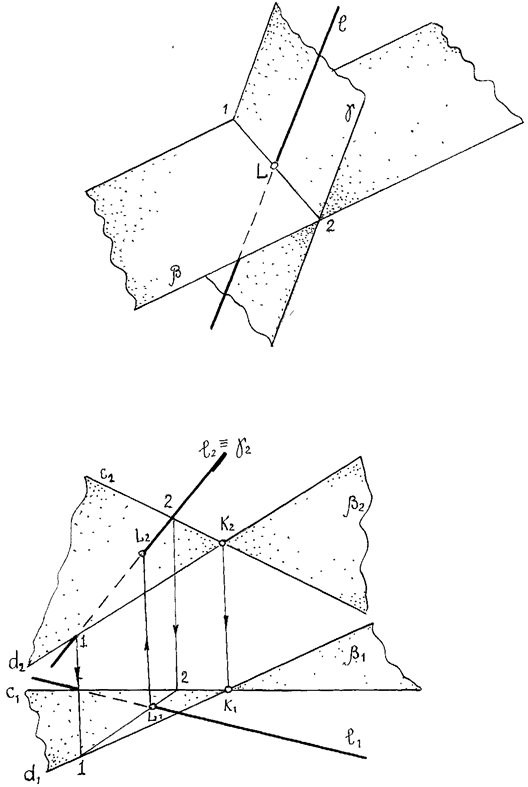
Пересечение двух плоскостей
Использование универсального алгоритма для решения задач по определению линии пересечения поверхностей проследим вначале на простых примерах пересечения двух плоскостей.
Две плоскости пересекаются по прямой линии, поэтому для ее определения достаточно найти две точки, принадлежащие одновременно каждой из заданных плоскостей.
Чтобы найти такие точки, достаточно ввести две вспомогательные секущие плоскости S2 и g2, т.е. дважды выполнить последовательность операций, предусмотренных алгоритмом:
Пример: Определить линию пересечения LK плоскостей a и b.
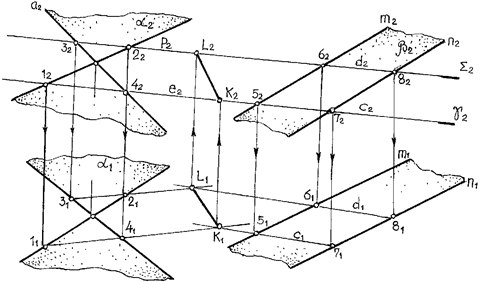
Рис. 26. Построение линии пересечения двух плоскостей
при помощи посредников
Решение представим в следующем виде.
| Словесное описание на языке начертательной геометрии: | Символическая запись на языке геометрии: |
| 1. Проводим фронтально-проецирую-щую плоскость g2. 2. Определим проекции прямых с1 и e1 и точку K1 пересечения этих прямых. 3. Проводим вторую фронтально-прое-цирующую плоскость S2. 4. Определяем проекцию прямых р1 и d1 и точку их пересечения L1. 5. Прямая l – есть линия пересечения двух плоскостей a и b. | Проводим: K = g Ç a и b; K1 = c1 Ç e1, L = S Ç a и b; L1 = d1 Ç p1, L = a Ç b. |
Определение точки пересечения линии с поверхностью
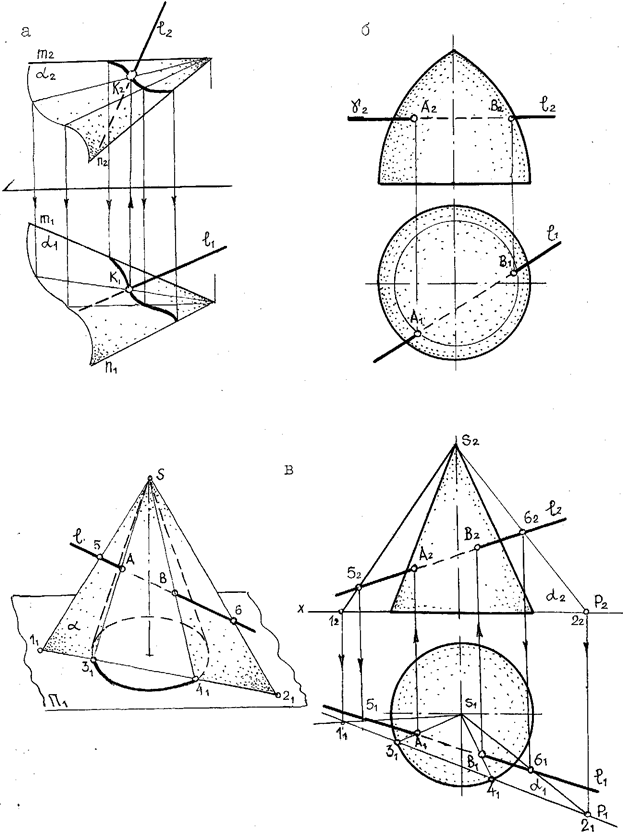
Для графического определения положения точек пересечения (встречи) линии с поверхностью необходимо выполнить ряд геометрических построении (риc. 28):
а) заключить данную линию во вспомогательную поверхность g ;
б) определить линию (линии) пересечения этой вспомогательной поверхности g с заданной поверхностью;
в) отметить точки, в которых пересекаются полученная линия пересечения с заданной (рис. 25).
Последовательность решения представим в следующем виде. В правой части приводится символическая запись, соответствующая смысловому содержанию, отмеченных этапов решения.
| Словесное описание на языке начертательной геометрии: | Символическая запись на языке теории множеств: |
| 1. Заключаем данную линию во вспомогательную поверхность. 2. Определяем линию пересечения вспомогательной поверхности с заданной поверхностью. 3. Отмечаем точки пересечения полученной линии пересечения с заданной. | 1. Заключаем а Ì g. 2. Определяем l = g Ç a. 3. Отмечаем К = а Ç l. |
Окончательный алгоритм для решения задачи определения точек пересечения линии с поверхностью в символической форме можно записать в виде <К…>= (g Ç a) Ç a.
Здесь, как и у алгоритма определения линии пересечения двух поверхностей, в зависимости от порядка и взаимного расположения, заданных кривой и поверхностью, множество искомых точек
Полученный алгоритм является универсальным, пригодным для решения задачи с любым вариантом задания исходных данных, в том числе и в случае, когда требуется определить точку пересечения (встречи) прямой с плоскостью.
Теперь проследим, как решается эта задача на эпюре Монжа (рис. 28).
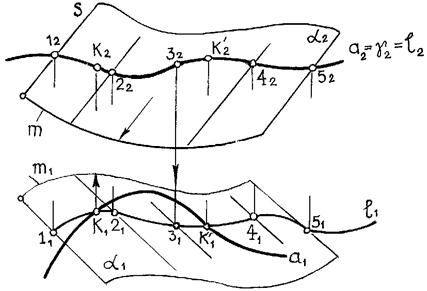
Пример 1: Определить точки пересечения кривой а с произвольной цилиндрической поверхностью a.
1. Заключаем кривую а2 во фронтально проецирующую цилиндрическую поверхность g2.
2. Определяем линию пересечения поверхностей g и a. Для этого отмечаем на а2 = g2 = l2 произвольные точки 12, 22, 32, 42, 52. Зная фронтальные проекции точек, находим их горизонтальные проекции 11, 21, 31, 41, 51. Соединив эти точки плавной кривой, получим горизонтальную проекцию l1 кривой l, по которой вспомогательная цилиндрическая поверхность g пересекает данную поверхность a.
3. Отмечаем точки K1, K’1 пересечения кривых a1 и l1. По горизонтальным проекциям определяем их фронтальные проекции К2, К’2.
Рис. 27. Пересечение кривой с поверхностью
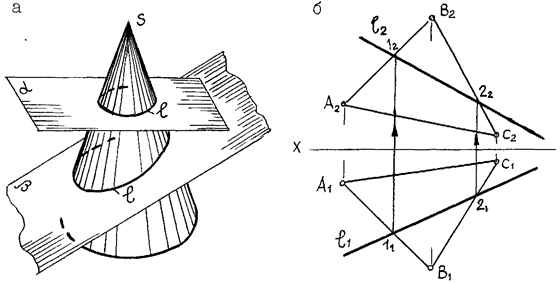
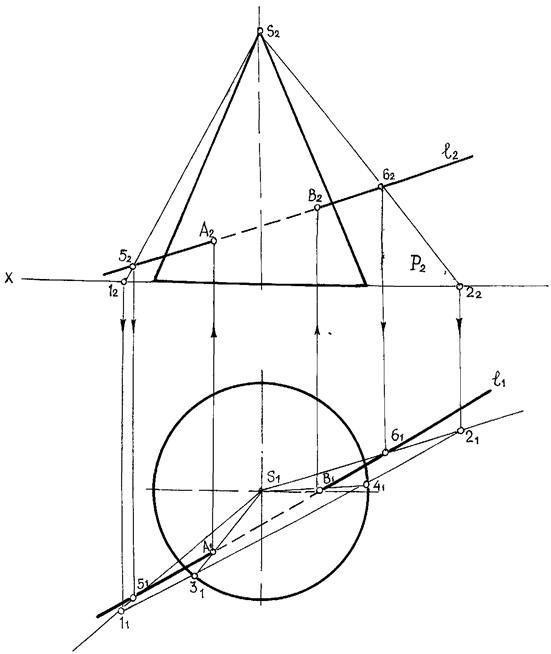
Пример 2: Определить точки пересечения прямой l с поверхностью прямого кругового конуса a (рис. 28).
Решение: Заключаем прямую l2 в плоскость Р, проходящую через вершину конической поверхности S. На рис. 28 плоскость Р задана пересекающимися прямыми, проходящими через произвольные точки 52 и 62 и верши-ну S. Две пересекающиеся прямые пересекутся с горизонтальной плоскостью в точках 12 и 22. Строим горизонтальную проекцию точек 51 и 61, которые соединим с вершиной S1 двумя образующими, и определим точки 11 и 21.
Через точки 11 и 21 проведем горизонтальный след плоскости P1, который пересечет окружность (основание конуса) в точках 31 и 41. Соединим точки 31 и 41 с S1, получим треугольник (простая фигура, полученная путем сечения плоскостью Р конической поверхности). Прямая l1 пересекается с полученным треугольником 31, S1 41 в точках A1 и B1. Точки А и В являются точками входа и выхода прямой на конической поверхности.
Рис. 28. Пересечение прямой линии с поверхностью конуса
Рис. 29. Пересечение прямой с поверхностью
Пересечение прямой с плоскостью
Задача на построение точки пересечения прямой линии с плоскостью является важнейшей из позиционных задач курса начертательной геометрии. Схема ее решения справедлива для решения задач на построение точек пересечения прямых с поверхностью, пересечение поверхности с плоскостью, построение линии пересечения поверхностей с линейчатыми поверхностями и т.п. В решении данной задачи используется проецирующая плоскость как вспомогательная.
Рассмотрим схему решения задачи на построение точки пересечения прямой с плоскостью (рис. 30, 31).
Дано: Плоскость b (с Ç d) прямая а (рис. 30).
Требуется: Построить точку пересечения прямой а с плоскостью b.
Так как а – прямая, то в алгоритме
g – плоскость. Поэтому и g Ç b = 1,2 – прямая.
В этом случае предписываемая алгоритмом последовательность выполнения геометрических построений будет иметь следующее содержание:
1) проводим через а1 горизонтально-проецирующую плоскость g1. Этим построением реализуется 1-й пункт алгоритма;
2) определяем фронтальную проекцию линии пересечения вспомогательной секущей плоскости g с данной плоскостью b-1, 2, используя для этого точки 11 и 21, в которых горизонтальная проекция g1 пересекает прямые с1 и d1;
3) выполнение третьего пункта алгоритма сводится к определению точки К2 = 1,2 Ç b. Зная K2, строим K1.
Алгоритм решения не меняется, если плоскость будет задана параллельными прямыми или прямыми, по которым она пересекает плоскости проекций (следы плоскости).
Рис. 30. Пересечение прямой с плоскостью
Рис. 31. Пересечение прямой l с плоскостью b
              |
                     |
 |
Вопросы для самоконтроля
1. Какие задачи относятся к метрическим?
2. Сформулировать определение принадлежности точки прямой, поверхности.
3. Сформулировать определение принадлежности прямой поверхности.
4. Изложите общий принцип построения обобщенного алгоритма для решения задачи по определению линии пересечения поверхностей.
5. Какие точки линии пересечения называются опорными?
6. В каких случаях плоскость пересекает поверхность прямого кругового конуса: по двум пересекающимся прямым; по окружности, эллипсу, параболе, гиперболе?
7. Чем следует руководствоваться при выборе вспомогательной секущей поверхности при определении точек пересечения линий с поверх-ностью?
Задача: Определить точку встречи прямой АВ с поверхностью сферы, с произвольной поверхностью вращения.
Позиционные задачи
Понятия и определения
Следует иметь в виду, что деление задач на позиционные и метрические является условным. Гели из всего многообразия задач позиционную группу можно выделить, то чисто метрические задачи встречаются очень редко; как правило, при решении метрических задач предварительно приходится выяснять позиционные отношения между геометрическими фигурами, входящими в условия задачи или построенными в процессе решения, г. е. решать позиционную задачу.
Несмотря на зго, распределение задач по отмеченным классам в методическом отношении имеет большой смысл, так как позволяет установить единые (обобщенные) алгоритмы, пригодные для решения широкого круга задач, входящих в один класс, и, как следствие, обеспечить простой и надежный поиск частного алгоритма для решения поставленной задачи.
В этой главе будут рассмотрены различные виды позиционных задач и указаны алгоритмы их решения. Под позиционными подразумеваются задачи, решение которых позволяет получить ответ о принадлежности элемента (точки) или подмножества (линии) множеству (поверхности). К позиционным относятся также задачи на определение общих элементов, принадлежащих различным геометрическим фигурам.
Первая группа задач может быть объединена под общим названием задачи на принадлежность (инцидентность). К ним, в частности, относятся задачи на определение:
1) принадлежности точки линии (А ∈ l);
2) принадлежности точки поверхности (А ∈ α);
3) принадлежности линии поверхности (l ⊂ α).
Ко второй группе относятся задачи на пересечение. Эта группа содержит также три типа задач:
1) на пересечение линии с линией (l ∩ m);
2) на пересечение поверхности с поверхностью (α ∩ β);
3) на пересечение линии с поверхностью (l ∩ α).
вости такого утверждения легко убедиться, перефразировав условия задач, входящих во вторую группу. Действительно:
1) задачу на определение точки пересечения линии с линией (l ∩ m) можно заменить задачей 1 (А ∈ l) первой группы: «определить точку, принадлежащую как линии l, так и линии m»;
3) задачу 3 второй группы «построить точку А пересечения линии l с поверхностью α (l ∩ α)» можно рассматривать как две задачи первой группы: А ∈ l (задача 1) и A ∈ α (задача 2).
Если учесть, что линию можно рассматривать как множество принадлежащих ей точек, то задача третьего типа (l ⊂ α) сводится к многократному решению задачи определения A ∈ α. Тогда окончательно получим следующее определение:
к позиционным относятся задачи, решение которых, в конечном счете, сводится: 1) к построению точки, принадлежащей линии (А ∈ l), и 2) к построению точки, принадлежащей поверхности (А ∈ α).
Решение таких задач базируется на инвариантном свойстве 2 (см. § 6) ортогонального проецирования, из которого вытекает:
A ∈ l ⇐⇒ (A’ ∈ l’) ∧ (А» ∈ l»); (2)
A ∈ α ⇐⇒ (A’ ∈ l’ ⊂ α’) ∧ (А» ∈ l» ⊂ α» ); (3)
Проследим на примерах, как решаются позиционные задачи.
Какие задачи относятся к позиционным?
Обсуждение вопроса:
Все многообразие позиционных задач можно отнести к трем группам:
1) задачи на построение линий пересечения двух поверхностей;
2) задачи на определение точек пересечения линий с поверхностью;
3) задачи на принадлежность точки поверхности.
Под позиционными подразумеваются задачи, решение которых позволяет получить ответ о принадлежности элемента (точки) или подмножества (линии) множеству (поверхности). К позиционным относятся также задачи на определение общих элементов, принадлежащих различным геометрическим фигурам.
Первая группа задач может быть объединена под общим названием задачи на принадлежность (инцидентность). К ним, в частности, относятся задачи на определение:
1) принадлежности точки линии (А ∈ l);
2) принадлежности точки поверхности (А ∈ α);
3) принадлежности линии поверхности (l ⊂ α).
Ко второй группе относятся задачи на пересечение. Эта группа содержит также три типа задач:
1) на пересечение линии с линией (l ∩ m);
2) на пересечение поверхности с поверхностью (α ∩ β);
3) на пересечение линии с поверхностью (l ∩ α).
Все задачи начертательной геометрии делятся на два больших класса: позиционные и метрические.
Позиционные – это задачи на определение занимаемого положения геометрической фигуры. Они бывают двух типов: задачи на инцидентность (принадлежность) и задачи на пересечение.