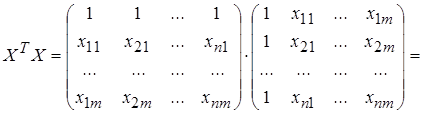при выполнении предпосылок метода наименьших квадратов оценки параметров регрессионной модели
При выполнении предпосылок метода наименьших квадратов оценки параметров регрессионной модели
2.3. Статистические свойства оценок метода наименьших квадратов
Поскольку полученные оценки a и b коэффициентов линейной регрессии основаны на статистических данных и являются случайными величинами, то естественно установить свойства этих оценок, как случайных величин. Более того, не выяснив этих свойств, невозможно сделать обоснованных выводов относительно качества и надежности полученных оценок. Необходимо, в частности, определить такие их статистические характеристики, как математическое ожидание и дисперсия. К желательным свойствам оценок относятся также несмещенность и состоятельность. Далее, если бы удалось определить вид распределения (плотности распределения) оценок, можно было бы построить доверительные интервалы для истинных значений параметров регрессии (то есть получить интервальные оценки коэффициентов) и реализовать процедуры проверки гипотез относительно их значений. Важную роль играет также изучение статистических свойств остатков оцененной регрессии.
Все эти задачи можно решить, основываясь на некоторых правдоподобных теоретических предпосылках (гипотезах) модели, выполнение которых на практике подлежит проверке с помощью специально разработанных для этого статистических процедур.
Предположение относительно независимых переменных
Предположения относительно случайной составляющей модели
При выполнении предпосылки относительно переменной x статистические свойства оценок параметров и зависимой переменной, а также остатков, целиком определяются вероятностными свойствами случайной составляющей регрессионной модели. Относительно случайной составляющей в классическом регрессионном анализе предполагают выполнение следующих условий, которые называются условиями Гаусса-Маркова и играют ключевую роль при изучении свойств оценок, полученных по методу наименьших квадратов.
1. Первое условие заключается в том, что математическое ожидание случайной составляющей во всех наблюдениях должно быть равно нулю. Формально это записывается так
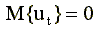 , для всех t =1,2,…,n. , для всех t =1,2,…,n. |
Смысл этого условия заключается в том, что не должно быть систематического смещения случайной составляющей. В линейной регрессии систематическое смещение линии регрессии учитывается с помощью введения параметра смещения 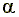
2. Дисперсия случайной составляющей постоянна для всех наблюдений (то есть не зависит от номера наблюдения). Это условие записывается так
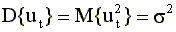 , где дисперсия , где дисперсия 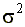 — величина постоянная. — величина постоянная. |
Это свойство дисперсии ошибок называется гомоскедастичностью (однородностью) (запомните этот термин).
Графическая иллюстрация понятий гомоскедастичность и гетероскедастичность
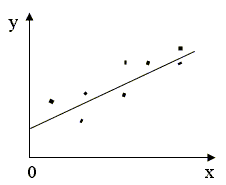
Рис. 2.6а. Гомоскедастичность
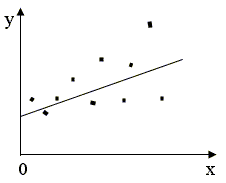
Рис. 2.6б. Гетероскедастичность
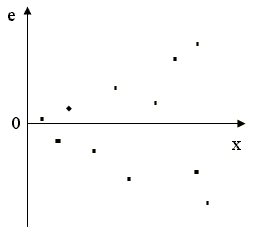
Рис. 2.6в. Гетероскедастичность
3. Случайные составляющие модели для различных наблюдений некоррелированы. Это условие записывается таким образом
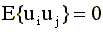 , для всех i не равных j (i, j=1,2,…,n). , для всех i не равных j (i, j=1,2,…,n). |
Выполнение этого условия означает отсутствие систематической (статистической) связи между значениями случайного члена в любых двух наблюдениях. Это свойство на практике также проверяется с помощью статистических процедур на основе анализа остатков модели. Если оно нарушается, то процедура оценки параметров должна быть скорректирована.
4. Четвертое условие Гаусса-Маркова записывается так
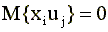 , для всех i и j, , для всех i и j, |
и означает, что объясняющие переменные и случайные составляющие некоррелированы для всех наблюдений. Ранее мы предположили, что объясняющая переменная в модели не является стохастической. В этом случае четвертое условие выполняется автоматически.
Дополнительное предположение о нормальном распределении ошибок
Данное предположение является, пожалуй, наиболее спорным. Дело в том, что предположение о нормальности можно считать правдоподобным, если значения случайной величины порождаются в результате воздействия большого количества независимых случайных факторов, каждый из которых не обязательно имеет нормальное распределение. Примером такого воздействия является так называемое броуновское движение (хаотичное движение малых частиц в жидкости как результат совокупного воздействия на частицу (ударов, соударения) большого количества молекул жидкости).
Если случайные величины в модели распределены по нормальному закону, то из свойств некоррелированности в третьем и четвертом условиях Гаусса-Маркова следует и независимость соответствующих случайных величин.
2.3.2. Свойства выборочных вариаций и ковариаций. Остаточные ошибки (остатки) модели, их свойства
Свойства выборочных вариаций (дисперсий) и ковариаций
Для дальнейшего изложения нам понадобиться установить ряд правил, которые можно использовать при преобразовании выражений, содержащих выборочные вариации и ковариации.
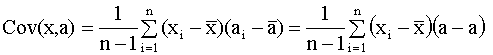 , , |
откуда следует свойство
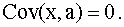
Далее, нетрудно видеть, что имеют место равенства
ОЦЕНКА ПАРАМЕТРОВ РЕГРЕССИОННОЙ МОДЕЛИ МЕТОДОМ НАИМЕНЬШИХ КВАДРАТОВ В EXCEL
Метод наименьших квадратов (МНК, англ. Ordinary Least Squares, OLS) — один из методов оценки параметров регрессионных моделей. Достоинством метода являются — статистические свойства МНК-оценок (при выполнении предпосылок Гаусса-Маркова — несмещенность и эффективность), простота математических выводов и практической реализации.
— для парной регрессии.
Смысл «наилучшего» приближения определяется выбором критерия. В методе наименьших квадратов — это сумма квадратов отклонений (остатков)
и оценки параметров и должны быть подобраны таким образом, чтобы функция была минимальна:
Для решения задачи (2) (задача на безусловный экстремум) составляются необходимые условия экстремума(First Order Condition):
которые, можно также записать следующим образом:
или в компактной форме:
Система (3) называется системой нормальных уравнений. В (3) столько уравнений, сколько параметров требуется оценить по выборочным данным. Из решения системы нормальных уравнений находятся МНК-оценки параметров:
Подстановка, полученного для выражения, во второе уравнение системы нормальных уравнений
приводит к следующей оценке параметра b
, — значения переменных центрированные по средним выборочным;
Реализация регрессионного анализа в программе MS Excel
Для проведения расчетов по линейному методу МНК можно использовать программу Microsoft Excel (входит в программный пакет Microsoft Office).
Наиболее просто реализуются вычисления коэффициентов линейной регрессионной модели (1).
Для этого можно использовать следующие встроенные функций MS Excel:
ОТРЕЗОК (диапозон_Y; диапазон_X)
НАКЛОН (диапазон_Y; диапазон_X)
КОРРЕЛ (диапазон_Y; диапазон_X)
Первая функция вычисляет свободный член уравнения регрессии ( в выражении (1)), вторая – наклон прямой (b в выражении (1)). Третья функция позволяет вычислить коэффициент корреляции.
Каждая из функций принимает два аргумента, разделяемых знаком точка с запятой “;”. Каждый из аргументов определяет диапазон ячеек, в котором находятся значения зависимой (диапазон_Y) и независимой (диапазон_Х) переменных. Диапазоны должны быть одинаковой формы (вектор-строка или вектор-столбец одинаковой длины).
В более общем виде линейный МНК может быть реализован с помощью встроенной функции ЛИНЕЙН, которая производит вычисления коэффициентов линейной регрессии и дополнительно рассчитывает ряд статистических показателей. Вычисленные коэффициенты регрессии и статистики возвращаются в виде массива чисел. Поскольку возвращается массив значений, функция должна задаваться в виде формулы массива.
Функция ЛИНЕЙН может принимать от одного до четырех аргументов. Обязателен только первый аргумент, остальные – необязательные:
ЛИНЕЙН (диапазон Y, [диапазон X], [константа], [статистика])
Диапазон Y — обязательный аргумент. Диапазон ячеек, содержащий множество значений зависимой переменной (y);
Диапазон Х — Диапазон ячеек, содержащий множество значений независимых переменных. Если переменных несколько, то они должны располагаться в смежных ячейках. Каждый диапазон значений независимой переменной должен иметь форму, аналогичную диапазону Y.
Константа. Необязательный аргумент. Логическое значение, которое указывает, требуется ли, чтобы константа была равна 0. Если аргумент константа имеет значение ИСТИНА или опущен, то свободный член вычисляется обычным образом.
Если аргумент константа имеет значение ЛОЖЬ, то значение полагается равным 0 и значения коэффициентов регрессии подбираются с этим условием.
Статистика. Необязательный аргумент. Логическое значение, которое указывает, требуется ли возвратить дополнительную регрессионную статистику. Если аргумент статистика имеет значение ИСТИНА, функция ЛИНЕЙН возвращает дополнительную регрессионную статистику. Возвращаемый массив чисел будет иметь следующий вид:
Если аргумент статистика имеет значение ЛОЖЬ или опущен, функция ЛИНЕЙН возвращает только коэффициенты (то есть, вектор-строку). Размер диапазона ячеек, в которые будет записан результат выполнения функции ЛИНЕЙН следующий:
1. Если статистика=ЛОЖЬ, то 1 строка и n столбцов (n-число определяемых параметров)
2. Если статистика=ИСТИНА, то 5 строк и k столбцов (число столбцов равно числу оцениваемых параметров, для парной регрессии — 2).
Описание значений, вычисляемых функцией приведены в таблице ниже.
Величина
Описание
Коэффициент детерминации. Он характеризует тесноту связи между результативным показателем и набором факторных показателей. Принимает только положительные значения в пределах от 0 до 1. Чем ближе значение коэффициента к 1, тем больше теснота связи. И, наоборот, чем ближе к 0, тем зависимость меньше.
Оценка ско возмущения.
F-статистика или F-наблюдаемое значение. F-статистика используется для определения того, является ли случайной наблюдаемая взаимосвязь между зависимой и независимой переменными.
Степени свободы. Степени свободы полезны для нахождения F-критических значений в статистической таблице. Для определения уровня надежности модели необходимо сравнить значения в таблице с F-статистикой, возвращаемой функцией ЛИНЕЙН.
Регрессионная сумма квадратов.
Остаточная сумма квадратов, равна сумме квадратов разностей для каждой точки между прогнозируемым значением y и фактическим значением y.
Пример. По территориям региона приводятся данные за 20ХХ г.
Среднедневная заработная плата, руб., y
Среднедушевой прожиточный минимум в день одного трудоспособного, руб., x
Оценка параметров регрессионной модели
ГЛАВА 3. МОДЕЛЬ МНОЖЕСТВЕННОЙ
ЛИНЕЙНОЙ РЕГРЕССИИ
Основные понятия и уравнения множественной регрессии
На любой экономический показатель чаще всего оказывает влияние не один, а несколько совокупно действующих факторов. Например, объем реализации (Y) для предприятий оптовой торговли может определяться уровнем цен (Х1), числом видов товаров (Х2), размером торговой площади (Х3) и товарных запасов (Х4). В целом объем спроса на какой-либо товар определяется не только его ценой (Х1), но и ценой на конкурирующие товары (Х2), располагаемым доходом потребителей (Х3), а также некоторыми другими факторами. Показатель инновационной активности современных предприятий зависит от затрат на исследования и разработки (Х1), на приобретение новых технологий (Х2), на приобретение программных продуктов и средств (Х3) и обучение и переподготовку кадров [7,28]. В этих случаях возникает необходимость рассмотрения моделей множественной (многофакторной, многомерной) регрессии [28].
Модель множественной линейной регрессии является естественным обобщением парной (однофакторной) линейной регрессионной модели. В общем случае ее теоретическое уравнение имеет вид:

где Х1, Х2,…, Хm – набор независимых переменных (факторов-аргументов); b0, b1, …, bm – набор (m + 1) параметров модели, подлежащих определению; ε – случайное отклонение (ошибка); Y – зависимая (объясняемая) переменная.
Для индивидуального i-го наблюдения (i = 1, 2, …, n) имеем:


Здесь bj называется j—м теоретическим коэффициентом регрессии (частичным коэффициентом регрессии).
Аналогично случаю парной регрессии, истинные значения параметров (коэффициентов) bj по выборочным данным получить невозможно. Поэтому для определения статистической взаимосвязи переменных Y и Х1, Х2, …, Хm оценивается эмпирическое уравнение множественной регрессионной модели

в котором 

Оцененное уравнение (3.4) в первую очередь должно описывать общий тренд (направление, тенденцию) изменения зависимой переменной Y. При этом необходимо иметь возможность рассчитать отклонения от этого тренда.
Самым распространенным методом оценки параметров уравнения множественной линейной регрессионной модели является метод наименьших квадратов (МНК). Напомним (см. раздел 2.4.1), что надежность оценок и статистических выводов, полученных с использованием МНК, обеспечивается при выполнении предпосылок Гаусса-Маркова. В случае множественной линейной регрессии к предпосылкам 1–4 необходимо добавить еще одну (пятую) – отсутствие мультиколлинеарности, что означает отсутствие линейной зависимости между объясняющими переменными в функциональной или статистической форме. Более подробно мультиколлинеарность объясняющих переменных будет рассмотрена в разделе (3.4). Модель, удовлетворяющая предпосылкам МНК, называется классической нормальной моделью множественной регрессии.
На практике часто бывает необходимо оценить силу влияния на зависимую переменную различных объясняющих (факторных) переменных. В этом случае используют стандартизованные коэффициенты регрессии 

Стандартизированный коэффициент регрессии определяется по формуле:

где S(xj) и S(y) – выборочные средние квадратичные отклонения (стандарты) соответствующей объясняющей и зависимой переменных.
Средний коэффициент эластичности

показывает, на сколько процентов (от средней) изменится в среднем зависимая переменная Y при увеличении только j-й объясняющей переменной на 1 %.
Для модели с двумя объясняющими (факторными) переменными 

Оценка параметров регрессионной модели
Для нахождения оценок параметров bj множественной линейной регрессионной модели (коэффициентов 


Тогда для нахождения коэффициентов 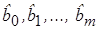

Необходимым условием минимума функции G является равенство нулю всех ее частных производных по 

Приравнивая (3.9) к нулю, получаем систему m + 1 линейных нормальных уравнений с m + 1 неизвестными для определения параметров модели:

где j = 1, 2, …, m – определяет набор регрессоров.
Следует заметить, что включение в модель новых объясняющих переменных усложняет расчет коэффициентов множественной линейной регрессии путем решения системы (3.10) по сравнению с парной моделью. Система из трех уравнений, соответствующая модели с двумя объясняющими переменными 
Тогда, вводя матричные обозначения, запишем:




Здесь Y – n-мерный вектор-столбец наблюдений зависимой переменной; Х – матрица размерности n · (m + 1) значений объясняющих переменных xij, в которой единица соответствует переменной при свободном члене 


В матричной форме модель (3.1) примет вид:
Оценкой этой модели по выборочным данным является уравнение (эмпирическая модель)

Предпосылки МНК (см. раздел 2.4.1.) в матричной форме можно записать следующим образом:
1. M(e) = 0; 2. D(e) = σ 2 I; 3. Матрица ковариаций V(e) = M(e · e T ) = σ 2 E,
где e = 
I = 
E = En×n = 

N(0, σ 2 Е); 5. r(X) = m + 1 > n – детерминированная матрица объясняющих переменных (регрессоров) имеет ранг r, равный числу определяемых параметров модели m + 1, кроме того, число имеющихся наблюдений каждой из объясняющих переменных и зависимой переменной превосходит ранг матрицы Х.
Выполнение пятой предпосылки означает линейную независимость объясняющих переменных (линейную независимость столбцов матрицы Х), т. е. отсутствие функциональной мультиколлинеарности.
Наша задача заключается в нахождении вектора оценок 
Воспользовавшись известными соотношениями матричной алгебры и правилами дифференцирования по векторному аргументу, получим необходимое условие минимума функции G (равенство нулю вектор-столбца частных производных 

откуда вытекает система нормальных уравнений в матричной форме для определения вектора

где Х Т – транспонированная матрица.
Решением уравнения (3.14) является вектор оценок:

Найдем матрицы, входящие в матричное уравнение (3.14):

Матрица Х Т Х образует симметричную матрицу сумм первых степеней, квадратов и попарных произведений n наблюдений объясняющих переменных.

Матрица Х Т Х представляет вектор-столбец произведений n наблюдений объясняющих и зависимой переменных.
Зная вектор коэффициентов множественной линейной регрессии 


Пример 3.1. Для иллюстрации получим формулы для расчета коэффициентов парной регрессии 

где detA – определитель матрицы Х Т Х; A * – присоединенная матрица (транспонированная матрица алгебраических дополнений).
Для данного примера:

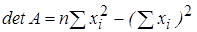


Тогда вектор оценок 

откуда следуют формулы (2.11) для определения параметров парной регрессионной модели.