расчет параметров решетки по дифрактограмме

Формулы для расчета параметров элементарных ячеек при различных сингониях кристаллических веществ

Введение

Точное определение параметров элементарной ячейки имеет большое практическое значение при изучении состава, структуры и физико-химических свойств многих кристаллических материалов, особенно металлов и сплавов. Так непрерывная регистрация изменений параметров решетки по мере изменения температуры позволяет определить коэффициент теплового расширения. Зависимость параметров элементарной ячейки от наличия примесей в исследуемом веществе позволяет определить состав твердых растворов и фазовые границы на диаграммах равновесия. С помощью точно измеренных размеров элементарной ячейки можно определить плотность, а также молекулярные веса кристаллов. Даже весьма незначительные изменения параметров решетки позволяют выявить причины появления внутренних напряжений в материале, которые часто приводят к дислокационным нарушениям и видимой трещиноватости.

Цель лабораторной работы — определение параметров элементарной ячейки поликристаллических веществ и материалов с помощью рентгеновского структурного анализа.

Метод испытаний

1. 1. Рентгеновский структурный анализ

Рентгеновский структурный анализ – методы исследования атомной структуры вещества с использованием явления дифракции рентгеновских лучей. Дифракция рентгеновских лучей возникает при их взаимодействии с электронными оболочками атомов исследуемого вещества. Дифракционная картина зависит от длины волны используемого излучения и атомного строения объекта. Для исследования атомной структуры применяют излучение с длиной волны ≈ 1 Ǻ (≈10 нм), т.е. сопоставимой с размерами атомов.

Кристаллические вещества обладают строгой периодичностью строения и представляют собой созданную самой природой дифракционную решетку для рентгеновского излучения.

Рис. 2.1.1. К выводу уравнения Вульфа-Брегга

Ход двух пучков рентгеновских лучей через систему из двух атомных плоскостей в кристалле схематично изображен на рис. 2.1.1. Разность хода двух пучков 2Δ. Так как , где d – расстояние между двумя соседними атомными плоскостями (межплоскостное расстояние), то разность хода равна . Для образования конструктивной интерференции (т. е. для отражения пучков в одной фазе) разность хода должна равняться :

(2.1.1)

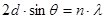
где d – межплоскостное расстояние, Å ;

– длина волны рентгеновского излучения, Å;

– угол падения (отражения) рентгеновских лучей, град.;

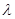
n – порядок отражения (1,2,3, ……)

Соотношение (2.1.1) называется условием Вульфа-Брэгга.

Условие Вульфа-Брэгга позволяет, зная величину 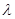и экспериментально измеренные углы , определить значения межплоскостных расстояний изучаемой кристаллической структуры вещества в узлах конструктивной интерференции. Интенсивность этой интерференции связана с симметрией кристаллической решетки. Совокупность значений межплоскостных расстояний с соответствующими значениями зарегистрированной интенсивности интерференции позволяют однозначно идентифицировать анализируемое кристаллическое вещество.

Для определения параметров элементарной ячейки кристаллических материалов необходимо выполнить индицирование атомных плоскостей, т.е. обозначить их индексами, которые определяют их пространственное положение в элементарной ячейке относительно выбранных в ней координатных осей (h, k, l – индексы Миллера).

Индексы Миллера определяют величину расстояния атома l_i, принадлежащего ячейке, от начала координат принятой системы координатных осей в единицах, кратных параметрам ячейки (рис. 2.1.2).

Рис. 2.1.2. Определение межплоскостных расстояний d через индексы Миллера hkl

Параметры элементарной ячейки можно определить, используя формулы для их расчета при различных сингониях кристаллического вещества, т.е. формах его кристаллической ячейки, связывающие эти параметры, межплоскостные расстояниями d_hkl и индексы отражающих плоскостей h, k, 1 (табл. 2.1.1).

Формулы для расчета параметров элементарных ячеек при различных сингониях кристаллических веществ

Сингония	Характеристики параметров элементарной ячейки	Взаимосвязь параметров элементарной ячейки с величиной межплоскостного расстояния
линейные соотношения	угловые соотношения
Кубическая
Тетрагональная
Гексагональная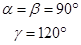
Ромбическая

Рентгеновский структурный анализ с 1916 г. начал применяться для определения межплоскостных расстояний и параметров элементарных ячеек моно- и поликристаллических веществ. В 50-х гг. XX в. начали бурно развиваться методы этого анализа с использованием ЭВМ в технике эксперимента и при обработке рентгеновских дифракционных картин. Результаты исследований практически для всех кристаллических веществ, а также кристаллических полимеров, аморфных тел и жидкостей широко представлены как в государственных, так и в международных стандартных справочных источниках.

1.2. Дифрактометрический метод рентгеновского структурного анализа

Основными приборами для выполнения рентгеновского структурного анализа дифрактометрическим методом являются:

• генераторное устройство с рентгеновской трубкой. Источником излучения электронов в рентгеновской трубке служит катод — вольфрамовая спираль, разогреваемая электрическим током. Материал анода (Fe, Со, Сu, Мо, Сг и др.) определяет длину волны излучения;

• гониометрическое устройство, с помощью которого осуществляется фокусировка рентгеновского пучка на поверхность образца и измерение углов падающего и дифрагированного лучей во время съемки;

• детектор излучения, сопряженный с регистрирующим устройством. В качестве регистрирующего устройства может служить самопишущий потенциометр, цифропечатающее устройство и запоминающее устройство ЭВМ.

На рис. 2.1.3 представлена блок-схема рентгеновского дифрактометра типа ДРОН, предназначенного для получения дифракционной картины в автоматическом режиме с записью дифрактограмм на ленту самописца.

Рис. 2.1.3. Блок-схема рентгеновского дифрактометра ДРОН-1: I – оперативный стол, II – гониометрическое устройство; III – счетнорегистрирующее устройство.

1 – сетевой щиток; 2 – стабилизатор напряжения ЗСНД-1М; 3 – автотрансформатор; 4 – пульт управления со стабилизатором анодного тока; 5 – генераторное устройство; 6 – рентгеновская трубка; 7 – образец; 8 – сцинтилляционный счетчик; 9 – блок сканирования; 10 – стабилизатор напряжения; II – блок питания; 12 – высоковольтный выпрямитель; 13 – генератор проверки; 14 – измеритель скорости счета; 15 – широкополосный усилитель; 16 – диффференциальный дискриминатор; 17 – пересчетный прибор; 18 – самопишущий потенциометр; 19 – цифропечатающее устройство

1.3. Требования к образцам

Для съемки на дифрактометре используется плоский образец. Чтобы увеличить количество кристаллитов, участвующих в формировании дифракционной картины, анализируемый материал измельчается. Затем его тщательно растирают со спиртом в агатовой ступке, а высохшую смесь наносят на плоскую поверхность подложки или изготавливают прессованную таблетку. Образец помещают в стандартную форму (кювету гониометра) таким образом, чтобы его поверхность была ровной и совпадала с верхним краем этой кюветы.

1.4. Съемка и расчет дифрактограмм

Кювета с образцом устанавливается в специальном держателе гониометра. С включением аппарата образец и счетчик начинают поворачиваться с заданными скоростями в горизонтальной плоскости вокруг общей вертикальной оси гониометра; угол падения лучей на плоскость образца постепенно возрастает. Интенсивность дифрагированных лучей последовательно под разными все увеличивающимися углами измеряется детектором излучения (сцинтилляционным счетчиком).

При повороте образца часть отражающих плоскостей кристаллитов вещества проходит через положение, при котором выполняется условие Вульфа-Брэгга.

В процессе съемки детектор излучения, вращающийся в два раза быстрее образца, пересекает все дифрагированные лучи. Его показания синхронно с вращением регистрируются на диаграммной ленте самопишущего устройства. В результате на этой ленте фиксируется дифрактограмма– характеристика зависимости интенсивности дифракционной картины от угла отражения (приложение 2.1.1, рис.1).

Интенсивность отраженных лучей прямо пропорциональна числу атомных плоскостей, попадающих в отражающее положение. Увеличению интенсивности дифрагированных лучей соответствует увеличивающаяся амплитуда отклонения пера самописца от фоновой линии.

Так как условие Вульфа-Брэгга определено для узких интервалов значений угла , то с учетом рассеяния дифракционная картина атомных плоскостей чаще всего имеет вид треугольника (дифракционного пика). Центр тяжести такого пика (или положение его вершины) фиксирует угол . Отметка углов на дифрактограмме обычно происходит через каждый градус поворота детектора излучения (угла 2 ), поэтому, чтобы рассчитать значение угла , зафиксированные значения угла необходимо разделить пополам.

Определив угол с точностью до 0,01° и зная длину волны излучения, можно рассчитать значения межплоскостных расстояний d для каждого дифракционного пика по формуле (2.1.1) или используя Универсальные таблицы, которые были составлены путем расчетов для условия Вульфа-Брэгга к наиболее распространенным длинам волн с целью повышения точности и экспрессности расчетов.

Интенсивность (высоту) дифракционных пиков I_i определяют с помощью линейки (например, в миллиметрах). Интенсивность самого мощного пика I_max принимают за 10 (или 100) единиц, интенсивность остальных I_i оценивается приблизительно в долях от этой величины (относительная интенсивность):

, доли ед. (2.1.3)

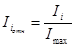
Сравнение совокупности значений межплоскостных расстояний d и соответствующих значений зарегистрированной относительной интенсивности интерференции I_отн с аналогичной совокупностью для анализируемого вещества, представленной в справочных источниках, дает возможность провести индицирование кристаллографических плоскостей и рассчитать параметры элементарной ячейки.

Источник

Форум химиков

параметр кристаллической решетки

параметр кристаллической решетки

Сообщение Elena » Ср фев 20, 2013 10:31 pm

Re: параметр кристаллической решетки

Сообщение МОNSТА » Чт фев 21, 2013 8:41 am

Re: параметр кристаллической решетки

Сообщение Elena » Чт фев 21, 2013 9:33 am

Спасибо! Это, действительно, кубическая гранецентрированная решетка.
Правильны ли мои расчеты?
Длина волны составляла 1,54 ангстрем. Для самого интенсивного пика n = 1?
По формуле Вульфа-Брэгга в моем случае получается d = 3,36 ангстрем (n = 1).
Параметр я посчитала по формуле a = d * (h^2 + k^2 + l^2)^(1/2) = 0,58 А.
С литературными данными все согласуется =))

А как быть с электронной дифракцией (второй рисунок)?

Re: параметр кристаллической решетки

Сообщение ИСН » Чт фев 21, 2013 11:07 am

Re: параметр кристаллической решетки

Сообщение Elena » Чт фев 21, 2013 11:47 am

Re: параметр кристаллической решетки

Сообщение ИСН » Чт фев 21, 2013 12:00 pm

Re: параметр кристаллической решетки

Сообщение Elena » Чт фев 21, 2013 12:13 pm

Re: параметр кристаллической решетки

Сообщение ИСН » Чт фев 21, 2013 12:50 pm

Re: параметр кристаллической решетки

Сообщение Elena » Чт фев 21, 2013 1:02 pm

Re: параметр кристаллической решетки

Сообщение ИСН » Чт фев 21, 2013 1:22 pm

Re: параметр кристаллической решетки

Сообщение Elena » Чт фев 21, 2013 1:24 pm

Re: параметр кристаллической решетки

Сообщение МОNSТА » Чт фев 21, 2013 2:23 pm

Re: параметр кристаллической решетки

Сообщение ИСН » Чт фев 21, 2013 3:12 pm

Re: параметр кристаллической решетки

Сообщение МОNSТА » Чт фев 21, 2013 3:24 pm

Re: параметр кристаллической решетки

Сообщение Elena » Чт фев 21, 2013 5:06 pm

Re: параметр кристаллической решетки

Сообщение ИСН » Чт фев 21, 2013 5:26 pm

Re: параметр кристаллической решетки

Сообщение Elena » Чт фев 21, 2013 5:50 pm

Re: параметр кристаллической решетки

Сообщение Engager » Сб фев 23, 2013 12:14 am

Дифракция электронов несколько отличается от дифракции рентгеновских лучей. Электроны разогнанные высокой разностью потенциалов обладают малым значение длинны волны Де Бройля. С учетом релятивистской поправки длинна волны электрона находится по выражению:

Где V0 разность потенциалов использованная для разгона элекрона. Типичное ускоряющее напряжение ПЭМ cоставляет 100 кВ, соответствующая длинна волны Де Бройля составляет 0.03701Å. Малая длинна волны обуславливает малые углы дифракции составляющие не более нескольких градусов. Учтя что для малых углов sin(theta) = theta, получаем упрощенное уравнение l/d = 2sin(theta) = 2*theta. Поскольку при дифракции электронов мы имеем дело с кольцами нам удобнее измерять радиусы колец. Для того чтобы связать угол дифракции с радиусом кольца воспользуемся простейшей геометрией:

В качестве живого примера могу привести вам следующую ситуацию (снято на ПЭМ при напряжении в 100 кВ):

Золото:

Исследуемая система:

Посмотрев соотношение радиусов колец приходим к выводу о ГЦК решетке исследуемого образца. Произведя указанные операции получаем:

hkl D(A)
111 3.1283333
200 2.72
220 1.9133333
311 1.6316667
222 1.5650000
400 1.3500000
331 1.2450000
420 1.2183333
422 1.1066667
333 1.0433333

Для ГЦК решетки постоянная решетки находится из величины d любой грани по формуле: a = d*sqrt(h2+k2+l2). Для грани (111) имеем a = d(111)*sqrt(3) = 5.4178A.
Да, и кстати, если потребуется вот таблица межплоскостных расстояний золота:

Gold (25C) Wyckoff
4.07825 4.07825 4.07825 90.0000 90.0000 90.0000
h k l d Intensity
1 1 1 2.35458 100
2 0 0 2.03912 51.362
2 2 0 1.44188 38.535
3 1 1 1.22964 47.262
2 2 2 1.17729 13.719
4 0 0 1.01956 6.417
3 3 1 0.93561 19.141
4 2 0 0.91192 17.506
4 2 2 0.83247 12.656
5 1 1 0.78486 10.198
3 3 3 0.78486 3.399
4 4 0 0.72094 3.696
5 3 1 0.68935 12.412
6 0 0 0.67971 1.467
4 4 2 0.67971 5.869

Надеюсь с дифракцией электронов теперь все станет яснее)))

Источник