сколько настраиваемых параметров имеет математическая модель нейрона
Математическая модель искусственного нейрона



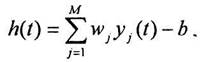 |
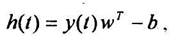 |
где T – знак транспортирования вектора или матрицы.
Выходной сигнал нейрона n(t+1) на следующем такте дискретного времени рассматривается как результат нелинейного преобразования потенциала h(t):
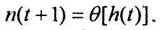 (3.3) (3.3) |
В работе [2] в качестве нелинейного преобразователя используется пороговая единичная функция:
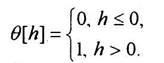 |
Функция Ө[h]называется активационной характеристикой, или передаточной функцией нейрона. Кроме рассмотренной выше пороговой функции, в нейронной сети могут быть использованы другие типы активационных характеристик. Обычно используются нелинейные функции, называемые сигмоидальными. Они обладают следующими свойствами:
· бесконечная числовая ось отображается сигмоидальной функцией на конечный интервал,
· сигмоидальная функция епрерывна и монотонно
возрастает.
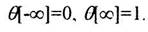 |
Обычно к указанным требованиям добавляются условия
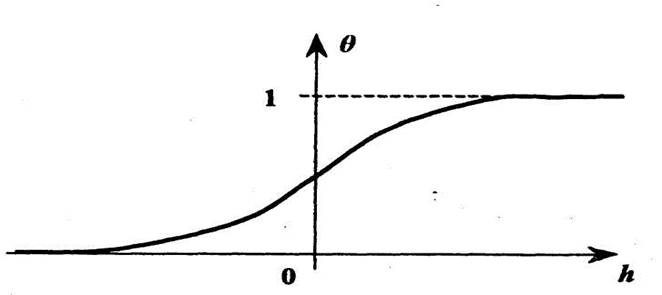
Если условия (3.5) не выполнены, то с помощью простейших линейных преобразований потенциала hони могут быть удовлетворены. На рис.1.5 представлен типовой пример сигмоидальной функции активации нейрона.
В практических приложениях можно встретить различные нелинейные характеристики Ө[h]:
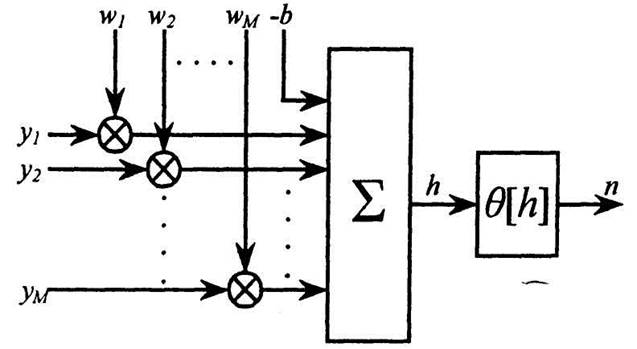 |
Рис. 1.4. Математическая модель технического нейрона
 |
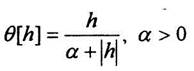 |
Рис. 1.5. Сигмоидальная активационная характеристика
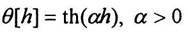 |
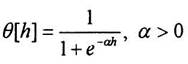 |
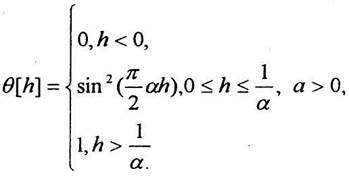 |
Активационная характеристика (3.8) носит название логистической..
Функция активации нейрона может быть невозрастающей в отличие от предыдущих примеров. В частности, может быть применена гауссова функция
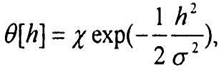 |
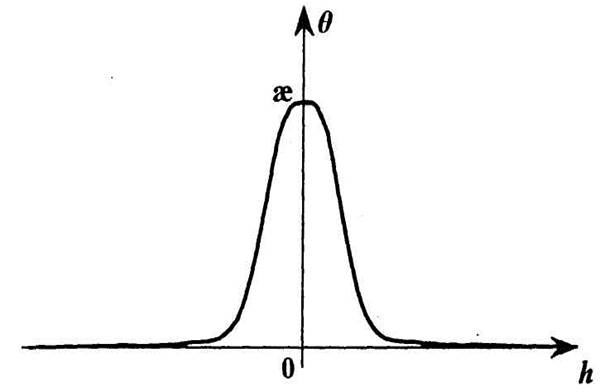 |
Рис. 1. 6. Гауссова активационная характеристика нейрона
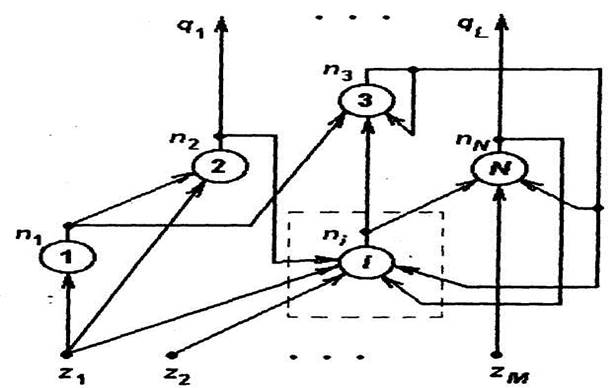 |
Рис. 1.7. Схема нейронной сети, содержащей N нейронов
AI Lab
Open Artificial Intelligence Laboratory
Обзор существующих моделей нейронов
Одним из важных направлений разработки интеллектуальных системявляется теория нейронных сетей. На сегодняшний день искусственные нейронные сети (ИНС) применяют для:
Искусственный нейрон имитирует в первом приближении свойства биологического нейрона. На вход искусственного нейрона поступает некоторое множество сигналов, каждый из которых является выходом другого нейрона.
Для того чтобы верно оценить какие существуют искусственные нейроны, что они позволяют реализовывать, как можно улучшить существующие модели нейронов и нейронных сетей и какими могут быть новые разработки в этой области, необходимо произвести их обзор и классификацию.
1 Классификация моделей нейронов
Возможно множество способов классификации моделей нейронов. Для лучшего понимания существующих достижений в сфере моделирования нейронов и нейронных сетей рассмотрим некоторые из возможных классификаций.
Во-первых, нейроны можно классифицировать на основе положения нейронов в топологии сети:
1) входные нейроны: принимают исходный вектор, кодирующий входной сигнал. Как правило, не выполняют вычислительных операций, а просто передают полученный входной сигнал на выход, возможно, усилив или ослабив его;
2) выходные нейроны: представляют выходы сети. В выходных нейронах могут производиться какие-либо вычислительные операции;
3) промежуточные нейроны — выполняют основные вычислительные операции.
Во-вторых, классификацию нейронов можно производить по степени разработки математического описания модели нейрона и качественного описания поведения нейрона (Рис.1):
Рис.1. Классификация нейронов по топологии и описанию
1) формальные (абстрактные) нейроны: отличаются хорошо разработанным математическим описанием, ноигнорируют многие свойства своего биологического двойника. Однако вопрос того, какие не описываемые формальными нейронами свойства биологических прототипов могут позволить существенно расширить сферу применения ИНС, или сложность решаемых ими задач, в общем случае остается открытым;
2) физиологические нейроны: отличаются количественным описанием поведения нейронов, порождены из экспериментов над биологическими нейронами;
3) феноменологические модели нейронов: не имеют строгой математической и опытной базы.
Формальные нейроны в свою очередь тоже могут быть разделены по нескольким признакам:
1.1) по виду функции активации;
1.2) по изменяемости весов входов:
1.3) в зависимости от вероятности значения выходного сигнала:
В-третьих, нейроны можно подразделять в зависимости от их аппаратной реализации:
1) цифровые модели – нейроны выполняются на микросхемах средней и высокой степени интеграции; на кристалле реализуется непосредственно нейронная сеть, т. е. отдельные нейроны не выделяются как самостоятельные единицы, т.к. модель разрабатывают для решения конкретных задач;
2) аналоговые модели: позволяют воспроизводить пространственное и временное суммированием возбуждающих сигналов, свойства абсолютной и относительной рефрактерности, процессы переработки информации в отдельном нейроне и при взаимодействии нейронов. Нейрон рассматривается как устройство, состояние которого может непрерывно меняться от полного покоя до некоторого максимального уровня возбуждения.
1.1. Формальные нейроны
Первая модель формального нейрона была разработана Маккалоком и Питтсом (Рис.2). Формальный нейрон представляет собой математическую модель простого процессора, имеющего несколько входов и один выход. Вектор входных сигналов, поступающих через дендриты, преобразуется нейроном в выходной сигнал, распространяющийся по аксону, с использованием трех функциональных блоков: локальной памяти, блока суммирования и блока нелинейного преобразования.
Вектор локальной памяти содержит информацию о весовых множителях, с которыми входные сигналы будут интерпретироваться нейроном. Эти переменные веса являются аналогом чувствительности пластических синаптических контактов. Выбором весов достигается та или иная интегральная функция нейрона.
В блоке суммирования происходит накопление общего входного сигнала (обычно обозначаемого символом net), равного взвешенной сумме входов.
В модели Маккалока-Питтса отсутствуют временные задержки входных сигналов, поэтому значение net определяет полное внешнее возбуждение, воспринятое нейроном. Отклик нейрон далее описывается по принципу «все или ничего», т. е. переменная подвергается нелинейному пороговому преобразованию, при котором выход (состояние активации нейрона) Y устанавливается равным единице, если net>, и Y=0 в обратном случае. Значение порога (часто полагаемое равным нулю) также хранится в локальной памяти. Таким образом, в модели Маккалока-Питтса используется пороговая активационная функция (по аналогии с электронными системами активационную функцию можно считать нелинейной усилительной характеристикой искусственного нейрона).
Используется при моделировании простых сетей, например, персептронов.
Помимо пороговой бинарной функции (функции Хевисайда), в качестве функции активации могут быть использованы:
1. Пороговая биполярная функция активации (сигнатурная).
Используется в нейронах, образующих линейные нейронные сети, а также в выходных слоях сетей на радиальных базисных функциях.
3. Сигмоидальная (S-образная) функция:
С. Гроссберг [9] обнаружил, что сигмоидальная функция обладает избирательной чувствительностью к сигналам разной интенсивности, что соответствует биологическим данным, и решает поставленную им дилемму шумового насыщения (т.е. обрабатывает как слабые, так и сильные сигналы). Наибольшая чувствительность наблюдается вблизи порога, где малые изменения сигнала net приводят к ощутимым изменениям выхода. Напротив, к вариациям сигнала в областях значительно выше или ниже порогового уровня сигмоидальная функция не чувствительна, так как ее производная при больших и малых аргументах стремится к нулю. Коэффициент усиления вычисляется как отношение приращения величины Y к вызвавшему его небольшому приращению величины net. Он выражается наклоном кривой при определенном уровне возбуждения и изменяется от малых значений при больших отрицательных возбуждениях (кривая почти горизонтальна) до максимального значения при нулевом возбуждении и снова уменьшается, когда возбуждение становится большим положительным.
То, что производная логистической функции может быть выражена через её значение облегчает использование этой функции при обучении нейронной сети по алгоритму обратного распространения. Логистическая функция в нейронных сетях используется наиболее часто.
б) гиперболический тангенс
Гиперболический тангенс симметричен относительно начала координат, и в точке net = 0 значение выходного сигнала Yравно нулю. В отличие от логистической функции, гиперболический тангенс принимает значения различных знаков, и это его свойство применяется для целого ряда сетей. Идеально подходит для пользовательской настройки многослойных персептронов.
4. Радиально-базисная функция передачи – функция, которая принимает в качестве аргумента расстояние между входным вектором и некоторым наперед заданным центром активационной функции. Значение этой функции тем выше, чем ближе входной вектор к центру. В качестве радиально-базисной чаще всего используют функцию Гаусса.
Сети с такими нейронами называются вероятностными и регрессионными. В реальных сетях активационная функция этих нейронов может отражать распределение вероятности какой-либо случайной величины, либо обозначать какие-либо эвристические зависимости между величинами.
5. Экспоненциальная функция.
Она используется, например, в первом скрытом слое нейронов вероятностных нейронных сетей. Достоинство таких сетей состоит в том, что их архитектура позволяет не только осуществить классификацию объектов, но и определить вероятность справедливости принимаемых решений.
Иногда используют экспоненциальные функции, выходы которых нормируются так, чтобы сумма всех активаций слоя равнялась 1. Их применяют в выходных слоях многослойных персептронов, специально сконструированных для задач классификации таким образом, чтобы выходы можно было интерпретировать как вероятности принадлежности к классу.
6. Квадратный корень [8].
Преобразует активации сети Кохонена, т.е. квадраты расстояний, в выходные значения, представляющие сами расстояния. Сеть Кохонена рассчитана на обучение без учителя и применяется для разведывательного анализа данных (распознавания кластеров в данных, устанавливания близости классов, решения задач классификации, обнаружения новых явлений).
7. Тригонометрический синус.
Используется при распознавании радиально распределенных данных.
8. Пилообразная функция [8].
Представляет кусочно-линейный вариант сигмоидальной функции. Обладает невысоким качеством обучения, но быстро работает.
При развитии модели Маккалока-Питтса были получены следующие модели нейронов (Рис.5):
Рис.5. Формальные нейроны
1.1.1 Адаптивный линейный нейрон (нейрон типа «адалайн»)
Это нейрон со структурой формального нейрона Маккалока-Питтса и сигнатурной функцией активации [1]. В данном нейроне в процессе минимизации квадратичной ошибки осуществляется адаптивный подбор весовых коэффициентов.
Для нахождения значений весовых коэффициентов в следующий момент применяют алгоритм градиентного обучения.
1.1.2 Нейрон Паде
Нейрон Паде может использоваться как обобщение нейрона типа «адалайн» в тех случаях, когда линейных функций становится недостаточно, в частности, в задачах интерполяции эмпирических зависимостей.
На практике такая модель практически не используется, т.к. она усложняет процесс построения нейросетевой модели, не внося значительных дополнительных возможностей [10].
1.1.3 Нейрон с квадратичным сумматором
Квадратичный сумматор может вычислять произвольный полином второго порядка от вектора входных сигналов.
Для многомерных нормальных распределений нейрон с квадратичным сумматором является наилучшим классификатором.
1.1.4 Сигма-Пи нейроны
Являются обобщением нейронов с линейной и квадратичной функциями активации на случай представления функции активации netполиномом степени N (N – число входов нейрона).
1.1.5. «Instar» и «Outstar » Гроссберга [1]
Могут обучаться как с учителем, так и без учителя. Применяется при решении задач классификации.
1.1.6. Модель нейрона Хебба
Структурная схема нейрона Хебба соответствует стандартной структуре формального нейрона. Д. Хебб заметил, что связь между двумя клетками усиливается, если обе клетки активируются одновременно, и предложил формальное правило обучения, в соответствии с которым вес wi нейрона изменяется пропорционально произведению его входного и выходного сигналов. Правило Хебба может применяться для нейронных сетей различных типов с любыми функциями активации отдельных нейронов.
При обучении с учителем вместо выходного сигнала yиспользуется ожидаемая от этого нейрона реакция d.
Упрощенная модель Ходжкина-Хаксли. Описывает такие свойства живого нейрона как генерация спайков и режим невосприимчивости к внешнему воздействию. Данная модель описывает влияние на возбудимость мембраны колебаний калиевой и кальциевой проводимостей.
Недостатком является то, что в рамках динамической модели с двухмерным фазовым пространством невозможно описать все детали динамики нейрона (например, хаотические колебании мембраны клетки) [11].
Представляет собой упрощенную модель, воспроизводящую основные свойства волн возбуждения в модели Ходжкина-Хаксли. Модель ФитцХью-Нагумо содержит две переменные: быструю переменную u, соответствующую мембранному потенциалу в полной модели, и медленную переменную v.
Принимать сигналы (импульсы) нейрон может с помощью входов. Каждый вход нейрона характеризуется весовым коэффициентом W (вес входа). Импульсы, поступая на вход нейрона, изменяют его текущее состояние. Эффект от импульса определяется типом входа, на который он поступил, весом этого входа а также текущим состоянием нейрона.
Одиночный импульс, пришедший на вход нейрона типа возбуждение, повышает величину потенциала нейрона на некоторое значение H, которое представляет собой произведение веса синапса, по которому пришел импульс, и функции f(P)(0,1). f(P) стремится к нулю при P стремящемся к Рmax.
Таким образом: если нейрон не возбуждён (потенциал равен нулю), то импульс увеличивает значение потенциала на величину, равную весу входа. Продолжительная периодическая импульсация поднимает потенциал «ступеньками», высота которых убывает с возрастанием самого потенциала. Высота ступенек становится равной нулю, когда потенциал достигает предельного максимального значения (Рmax). При данном задании функции, потенциал может превышать максимальное значение на величину, пренебрежимо малую.
Если на вход возбуждения нейрона последовательно подавать импульсы так, что бы либо их частота или вес входа компенсировали коэффициент затухания потенциала, то потенциал будет ступенчато возрастать.
Сходным образом ведёт себя вход торможения. Однако его роль заключается в уменьшении потенциала на величину H, которая рассчитывается аналогично (меняются только знак аргумента функции fи в роли ограничителя выступает Рmin). Если на вход торможения нейрона последовательно подавать импульсы так, что бы либо их частота или вес входа компенсировали коэффициент затухания потенциала (с обратным знаком), то потенциал будет ступенчато убывать
Изменение значений порога осуществляется импульсацией на входы регуляции и запрета. Импульс, поступивший на вход регуляции, уменьшает значение порога на величину H, которая рассчитывается также как Hдля тормозящего входа. Соответственно запрет увеличивает значение порога на величину H и вычисляется аналогично величине Hвозбуждающего входа.
Особенным образом работает вход памяти. Аналогично возбуждению он увеличивает потенциал, но приращение потенциала теперь зависит не только от веса входа, но также от текущего состояния коэффициента обученности. Коэффициент обученности в отличие от веса меняет своё значение динамически в процессе работы нейронной сети. Он может принимать значения в диапазоне от 0 до 1.
Если µ = 0, то вход считается необученным – в этом случае импульсация на этот вход не оказывает никакого влияния на состояние нейрона. Максимально обученный вход (µ = 1) работает аналогично входу возбуждения с весом W, пока значение µ снова не изменится (уменьшится).
Обучение, переобучение, разобучение – механизмы, регулирующие значение µ и, как следствие, работу входов памяти нейрона.
Обучение входа – увеличение µ на некоторую постоянную величину ∆µ+ (очевидно меньшую единицы), так называемую, способность к обучению. Эта величина неизменна и зафиксирована в значении ∆µ+ = 0,2. Обучение происходит при одновременном выполнении условий:
1) на данный вход поступил сигнал
2) сигнал на вход памяти был подкреплён сигналом с входа возбуждения (сигнал на возбуждение должен прийти не позже чем через время ∆T)
3) значение порога в этот момент было меньше, чем порог покоя (что возможно только при наличии регулирующей импульсации).
Разобучение – уменьшение µ, происходит в тех случаях, когда сигнал, поступивший на вход памяти, не был подкреплён последующим сигналом на вход возбуждения, или не сопровождался регулирующей импульсацией (при этом T ≥T0). В этой ситуации значение µ уменьшится на ∆µ-.
Таким образом, вход памяти отличается от входа возбуждения умением менять значимость своего вклада в общий потенциал в зависимости от характера импульсации.
Помимо общей для всех типов входов весовой характеристики W и частных характеристик входов типа память (µ, ∆µ+, ∆µ-) каждый вход также характеризуется величиной Delay. Delay определяет задержку поступления импульсации с одного нейрона на другой.
В модели это реализуется следующим образом: каждый вход запоминает импульс, поступивший на него, но эффект от него рассчитывает лишь спустя время Delay.
Генерация импульсов происходит, если величина ∆Ω = P-Tположительна, т.е. потенциал превысил порог. Частота генерации импульсов зависит от ∆Ω линейно.
Ограничения на частоту импульсации вытекают из верхнего ограничения на потенциал и нижнего ограничения на порог (Pmax, Tmin).
Математическая модель составлялась на основе знаний о работе реального биологического нейрона, с некоторыми принятыми упрощениями.
2 Заключение
На сегодняшний день создано большое количество моделей отдельных нейронов и моделей ИНС. В данной работе была предпринята попытка обобщить накопленные знания, касающиеся отдельных искусственных нейронов, и, исходя из этой цели, для существующих моделей нейроновбылиприведены различные классификации: по положению нейронов в топологии сети, в зависимости от аппаратной реализации нейронов и по степени разработки математического описания модели нейрона и качественного описания его поведения. По последнему критерию нейроны разделены на формальные (для которых в свою очередь также приводится классификация по нескольким критериям), физиологические и феноменологические.
В результате обзора существующих моделей становится видно, что существует достаточное количество нейронов, описывающих естественный нейрон очень упрощенно. Они нашли свое применение в области распознавания образов, для решения задач классификации и т.д. Также существует множество моделей, которые при описании нейрона ставят своей целью количественное описание поведения нейрона. Однако до сих пор остается непонятным, приводит ли усложнение нейрона, попытки отображения им все новых свойств естественного нейрона, к существенному прогрессу и улучшению результатов решаемых нейронами задач.
Краткий курс машинного обучения или как создать нейронную сеть для решения скоринг задачи
Мы часто слышим такие словесные конструкции, как «машинное обучение», «нейронные сети». Эти выражения уже плотно вошли в общественное сознание и чаще всего ассоциируются с распознаванием образов и речи, с генерацией человекоподобного текста. На самом деле алгоритмы машинного обучения могут решать множество различных типов задач, в том числе помогать малому бизнесу, интернет-изданию, да чему угодно. В этой статье я расскажу как создать нейросеть, которая способна решить реальную бизнес-задачу по созданию скоринговой модели. Мы рассмотрим все этапы: от подготовки данных до создания модели и оценки ее качества.
Если тебе интересно машинное обучение, то приглашаю в «Мишин Лернинг» — мой субъективный телеграм-канал об искусстве глубокого обучения, нейронных сетях и новостях из мира искусственного интеллекта.
Вопросы, которые разобраны в статье:
• Как собрать и подготовить данные для построения модели?
• Что такое нейронная сеть и как она устроена?
• Как написать свою нейронную сеть с нуля?
• Как правильно обучить нейронную сеть на имеющихся данных?
• Как интерпретировать модель и ее результаты?
• Как корректно оценить качество модели?
«Вопрос о том, может ли компьютер думать, не более интересен,
чем вопрос о том, может ли субмарина плавать».
Эдсгер Вибе Дейкстра
Во многих компаниях, менеджеры по продажам общаются с потенциальными клиентами, проводят им демонстрации, рассказывают о продукте. Отдают, так сказать, свою душу по сотому разу на растерзание тем, кто, возможно, попал в их руки совершенно случайно. Часто клиенты недостаточно понимают, что им нужно, или то, что продукт может им дать. Общение с такими клиентами не приносит ни удовольствия, ни прибыли. А самое неприятное то, что из-за ограничения по времени, можно не уделить достаточно внимания действительно важному клиенту и упустить сделку.
Я математик-программист в сервисе seo-аналитики Serpstat. Недавно я получил интересную задачу по улучшению уже существующей и работающей у нас скоринговой модели, по-новому оценив факторы, которые влияют на успех продажи. Скоринг считался на основе анкетирования наших клиентов, и каждый пункт, в зависимости от ответа на вопрос, вносил определенное количество очков в суммарный балл. Все эти баллы за разные вопросы расставлялись на основе статистических гипотез. Скоринговая модель использовалась, время шло, данные собирались и в один прекрасный день попали ко мне. Теперь, когда у меня появилась достаточная выборка, можно было смело строить гипотезы, используя алгоритмы машинного обучения.
Я расскажу вам, как мы построили свою скоринг модель. Это реальный кейс с реальными данными, со всеми трудностями и ограничениями, с которыми мы столкнулись в реальном бизнесе. Итак, обо всем по порядку.
Мы подробно остановимся на всех этапах работы:
▸ Сбор данных
▸ Препроцессинг
▸ Построение модели
▸ Анализ качества и интерпретация модели
Рассмотрим устройство, создание и обучение нейросети. Все это я описываю, решая реальную скоринговую задачу, и постоянно подкрепляю новую теорию примером.
Сбор данных
Вначале нужно понять, какие вопросы будут представлять клиента (или просто объект) в будущей модели. К задаче подходим серьезно, так как на ее основании строится дальнейший процесс. Во-первых, нужно не упустить важные признаки, описывающие объект, во-вторых, создать жесткие критерии для принятия решения о признаке. Основываясь на опыте, я могу выделить три категории вопросов:
Основываясь на вышесказанном, попробуем представить формат данных с типами вопросов, для дальнейшей подготовки:
| класс: (категория) | цвет: (категория) | вкус: (категория) | вес: (число) | твердый: (bool) |
|---|---|---|---|---|
| — | красный | кислый | 4.23 | да |
| — | зеленый | горький | 3.15 | нет |
| + | зеленый | горький | 4.14 | да |
| + | синий | сладкий | 4.38 | нет |
| — | зеленый | соленый | 3.62 | нет |
Таблица 1 — Пример данных обучающей выборки до препроцессинга
Препроцессинг
После того как данные собраны, их необходимо подготовить. Этот этап называется препроцессинг. Основная задача препроцессинга — отображение данных в формат пригодный для обучения модели. Можно выделить три основных манипуляции над данными на этапе препроцессинга:
Теперь мы научились превращать категориальные признаки в обычные числовые вектора, а это очень полезно. Проведя все манипуляции над данными, мы получим обучающую выборку, подходящую любой модели. В нашем случае, после применения унитарной кодировки и нормализации данные выглядят так:
| class: | red: | green: | blue: | bitter: | sweet: | salti: | sour: | weight: | solid: |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0.23 | 1 |
| 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | -0.85 | 0 |
| 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0.14 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0.38 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | -0.48 | 0 |
Таблица 2 — Пример данных обучающей выборки после препроцессинга
Можно сказать, что препроцессинг — это процесс отображения понятных нам данных в менее удобную для человека, но зато в излюбленную машинами форму.
Формула скоринга чаще всего представляет из себя следующую линейную модель:
Где, k — это номер вопроса в анкете, wk — коэффициент вклада ответа на этот k-ый вопрос в суммарный скоринг, |w| — количество вопросов (или коэффициентов), xk — ответ на этот вопрос. При этом вопросы могут быть любыми, как мы и обсуждали: булевыми(да или нет, 1 или 0), числовыми (например, рост = 175) или категориальными, но представленными в виде унитарной кодировки (зеленый из перечня: красный, зеленый или синий = [0, 1, 0]). При этом можно считать, что категориальные вопросы распадаются на столько булевых, сколько категорий присутствует в вариантах ответа (например: клиент красный? клиент зеленый? клиент синий?).
Выбор модели
Теперь самое важное: выбор модели. На сегодняшний день существует множество алгоритмов машинного обучения, на основе которых можно построить скоринг модель: Decision Tree (дерево принятия решений), KNN (метод k-ближайших соседей), SVM (метод опорных векторов), NN (нейросеть). И выбор модели стоит основывать на том, чего мы от нее хотим. Во-первых, насколько решения, повлиявшие на результаты модели, должны быть понятными. Другими словами, насколько нам важно иметь возможность интерпретировать структуру модели.

Рис. 1 — Зависимость гибкости алгоритма машинного обучения и интерпретируемости полученной модели
Кроме того, не все модели легко построить, для некоторых требуются весьма специфические навыки и очень-очень мощное железо. Но самое важное — это внедрение построенной модели. Бывает так, что бизнес-процесс уже налажен, и внедрение какой-то сложной модели попросту невозможно. Или требуется именно линейная модель, в которой клиенты, отвечая на вопросы, получают положительные или отрицательные баллы в зависимости от варианта ответа. Иногда, напротив, есть возможность внедрения, и даже требуется сложная модель, учитывающая очень неочевидные сочетания входных параметров, находящая взаимосвязи между ними. Итак, что же выбрать?
В выборе алгоритма машинного обучения мы остановились на нейронной сети. Почему? Во-первых, сейчас существует много крутых фреймворков, таких как TensorFlow, Theano. Они дают возможность очень глубоко и серьезно настраивать архитектуру и параметры обучения. Во-вторых, возможность менять устройство модели от однослойной нейронной сети, которая, кстати, неплохо интерпретируема, до многослойной, обладающей отличной способностью находить нелинейные зависимости, меняя при этом всего пару строчек кода. К тому же, обученную однослойную нейросеть можно превратить в классическую аддитивную скоринг модель, складывающую баллы за ответы на разные вопросы анкетирования, но об этом чуть позже.
Теперь немного теории. Если для вас такие вещи, как нейрон, функция активации, функция потери, градиентный спуск и метод обратного распространения ошибки — родные слова, то можете смело это все пропускать. Если нет, добро пожаловать в краткий курс искусственных нейросетей.
Краткий курс искусственных нейронных сетей
Начнем с того, что искусственные нейронные сети (ИНС) — это математические модели организации реальных биологических нейронных сетей (БНС). Но в отличие от математических моделей БНС, ИНС не требует точное описание всех химических и физических процессов, таких как описание «поджигания» потенциала действия (ПД), работы нейромедиаторов, ионных каналов, вторичных посредников, белков транспортеров и пр. От ИНС требуется схожесть с работой реальных БНС только на функциональном, а не на физическом уровне.
Базовый элемент нейросети — нейрон. Попробуем составить самую простую функциональную математическую модель нейрона. Для этого опишем в общих чертах функционирование биологического нейрона.

Рис. 2 — Типичная структура биологического нейрона
Как мы видим, структуру биологического нейрона можно упростить до следующей: дендриты, тело нейрона и аксон. Дендриты — ветвящиеся отростки, собирающие информацию со входа в нейрон (это может быть внешняя информация с рецепторов, например с колбочки в случае цвета или внутренняя информация от другого нейрона). В том случае, если входящая информация активировала нейрон (в биологическом случае — потенциал стал выше какого-то порога), рождается волна возбуждения (ПД), которая распространяется по мембране тела нейрона, а затем через аксон, посредством выброса нейромедиатора, передает сигнал другим нервным клетками или тканям.
Затем из этих минимальных структурных единиц собирают классические искусственные нейронные сети. Принята следующая терминология:
Именно благодаря наличию скрытых ассоциативных слоев, искусственная нейронная сеть способна строить гипотезы, основанные на нахождении сложных зависимостей. Например, для сверточных нейросетей, распознающих изображения, на входной слой будут подаваться значения яркости пикселей изображения, а выходной слой будет содержать нейроны, отвечающие за конкретные классы (человек, машина, дерево, дом и т. д.) В процессе обучения в близких к «рецепторам» скрытых слоях начнут «сами собой» появляться (специализироваться) нейроны, возбуждающиеся от прямых линий, разного угла наклона, затем реагирующие на углы, квадраты, окружности, примитивные паттерны: чередующиеся полоски, геометрические сетчатые орнаменты. Ближе к выходным слоям — нейроны, реагирующие, например, на глаз, колесо, нос, крыло, лист, лицо и т. д.

Рис. 5 — Образование иерархических ассоциаций в процессе обучения сверточной нейронной сети
Проводя биологическую аналогию, хочется сослаться на слова замечательного нейрофизиолога Вячеслава Альбертовича Дубынина, касающиеся речевой модели:
«Наш мозг способен создавать, генерировать такие слова, которые обобщают слова более низкого уровня. Скажем, зайчик, мячик, кубики, кукла ― игрушки; игрушки, одежда, мебель ― это предметы; а предметы, дома, люди ― это объекты окружающей среды. И так еще немного, и мы дойдем до абстрактных философских понятий, математических, физических. То есть речевое обобщение ― это очень важное свойство нашей ассоциативной теменной коры, и оно, вдобавок, многоуровневое и позволяет речевую модель внешнего мира формировать, как целостность. В какой-то момент оказывается, что нервные импульсы способны очень активно двигаться по этой речевой модели, и это движение мы и называем гордым словом «мышление».
Много теории?! Но есть и хорошие новости: в самом простом случае вся нейросеть может быть представлена одним единственным нейроном! При этом даже один нейрон часто хорошо справляется с задачей, особенно, когда дело касается распознавания класса объекта в пространстве, в котором объекты этих классов являются линейно сепарабельными. Часто добиться линейно сепарабельности можно повысив размерность пространства, о чем было написано выше, и ограничиться всего одним нейроном. Но иногда проще добавить в нейросеть пару скрытых слоев и не требовать от выборки линейной сепарабельности.
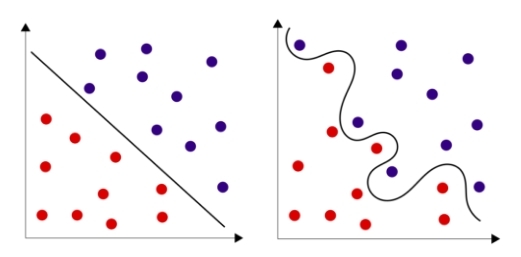
Рис. 6 — Линейно разделимые множества и линейно неразделимые множества
Как видно из формулы, результат работы нейрона — это функция активации (часто обозначаемая через ) от суммы произведения входных параметров на искомые в процессе обучения коэффициенты. Разберемся что же такое функция активации.
Так как на вход нейросети могут поступать любые действительные значения, и коэффициенты матрицы весов тоже могут быть какими угодно, то и результатом суммы их произведений может быть любое вещественное число от минус до плюс бесконечности. У каждого элемента обучающей выборки есть значение класса относительно этого нейрона (ноль или один). Желательно получить от нейрона значение в этом же диапазоне от нуля до единицы, и принять решение о классе, в зависимости от того, к чему это значение ближе. Еще лучше интерпретировать это значение как вероятность того, что элемент относится к этому классу. Значит, нам нужна такая монотонная гладкая функция, которая будет отображать элементы из множества вещественных чисел в область от нуля до единицы. На эту должность отлично подходит так называемая сигмоида.

Рис. 7 — График логистической кривой, одной из самых классических представительниц класса сигмоид
Вот самое важное, что стоит извлечь из написанного выше: «Обучение нейросети (синаптическое обучение) должно свестись к оптимальному подбору коэффициентов матрицы весов с целью минимизации допускаемой ошибки.» В случае однослойной нейросети эти коэффициенты можно интерпретировать как вклад параметров элемента в вероятность принадлежности к конкретному классу.
Результат работы нейросети принято называть гипотезой (англ. hypothesis). Обозначают через h(X), показывая зависимость гипотезы от входных признаков (параметров) объекта. Почему гипотезой? Так уж исторически сложилось. Лично мне этот термин нравится. В итоге мы хотим, чтобы гипотезы нейросети как можно больше соответствовали действительности (реальным классам объектов). Собственно здесь и рождается основная идея обучения на опыте. Теперь нам потребуется мера, описывающая качество нейросети. Этот функционал обычно называют «функцией потерь» (англ. loss function). Функционал обычно обозначают через J(W), показывая его зависимость от коэффициентов матрицы весов. Чем функционал меньше, тем реже наша нейросеть ошибается и тем это лучше. Именно к минимизации этого функционала и сводится обучение. В зависимости от коэффициентов матрицы весов нейросеть может иметь разную точность. Процесс обучения — это движение по гиперповерхности функционала потери, целью которого является минимизация этого функционала.

Рис. 8 — Процесс обучения, как градиентный спуск к локальному минимуму функционала потери
Обычно коэффициенты матрицы весов инициализируются случайным образом. В процессе обучения коэффициенты меняются. На графике показаны два разных итерационных пути обучения как изменение коэффициентов w1 и w2 матрицы весов нейросети, проинициализированных в соседстве.
Теперь собственно о том, как обучить нейросеть. Для этого существует множество вариантов, но я расскажу о двух: эволюционный (генетический) алгоритм и метод градиентного спуска. Эволюционные алгоритмы — это направление в искусственном интеллекте, которое основывается на моделировании естественного отбора. Раньше такой подход использовался для тренировки глубинных слоев нейросети. Эволюционные алгоритмы полностью уступили свое место оптимизаторам на основе градиентного спуска для задачи обучения глубох нейронных сетей, но они по-прежнему могут использоваться для образовательных целей: эволюционные алгоритмы очень просты в понимании, и с них лучше начинать новичкам, их стоит знать для дальнейшего сравнения вычислительной сложности и сходимости с другими (популярными ныне) методами. Метод градиентного спуска и обратного распространения ошибки более сложный, но зато один из самых эффективных и популярных методов обучения, наследниками которого являются популярные сейчас NAG, Adagrad, Adadelta, RMSprop, Adam, Nadam и т.д.
Эволюционное обучение
В рамках этого метода оперируем следующей терминологией: коэффициенты матрицы весов — геном, один коэффициент — ген, «перевернутая вниз головой» функция потерь — ландшафт приспособленности (тут мы уже ищем локальный максимум, но это всего лишь условность). Этот метод и вправду очень простой. После того как мы выбрали топологию (устройство) нейросети, необходимо сделать следующее:



