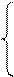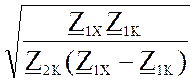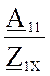сколько опытов необходимо для определения параметров симметричного линейного четырехполюсника

Экспериментальное определение коэффициентов четырёхполюсника

Страницы работы

Содержание работы

Экспериментальное определение коэффициентов четырёхполюсника А₁₁, А₁₂, А₂₁, А₂₂

Для определения коэффициентов четырёхполюсника можно использовать результаты любых трёх опытов из следующих четырёх:

1. прямой холостой ход (ХХ);

2. прямое короткое замыкание (КЗ),

Для симметричного четырёхполюсника достаточно первых двух опытов. Получим формулы для определения коэффициентов по результатам 1, 2 и 4 опытов.

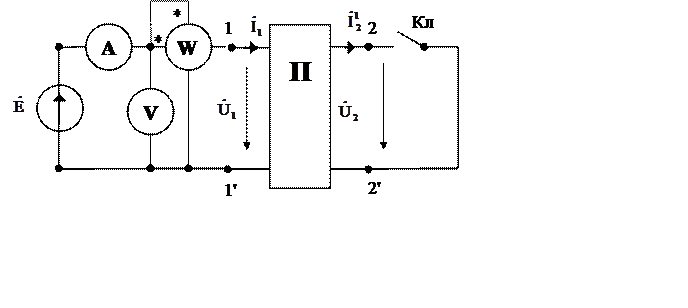1. Прямой ХХ четырёхполюсника (рис. 1, Кл. разомкнут).

Z_H= ¥, поэтому 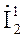= 0.

Уравнения типа «А» четырехполюсника:

= A₁₁ + A₁₂ , (1)

= A₁₂ + A₂₂ , (2)

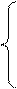
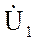
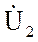
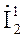
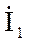
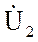
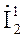
Тогда уравнения (1) и (2) принимают вид:

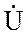
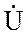
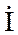
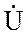
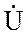
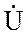
_1X = A_{11 2X},

_1X = A_{21 2X}.

A₁₁ = _1X /_2X, (3)

Согласно (3) и (4) находятся A₁₁ и A₂₁ только у четырёхполюсника постоянного тока. Для четырёхполюсника переменного тока приборы показывают только лишь модули комплексов действующих значений напряжения и тока, а не сами комплексы. Поэтому в опыте ХХ по показаниям трёх приборов (амперметра, вольтметра и ваттметра) находят комплекс входного сопротивления Z_1X, а его связь с коэффициентами:

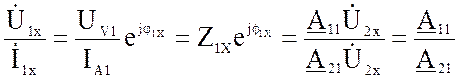
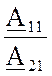
Z_1X = ; Z_1X = (5)

где U_V1, I_A1 и P_W1— показания вольтметра, амперметра и ваттметра в режиме прямого ХХ,

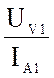
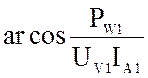
Z_1X = и j_1Х = модуль и аргумент входного сопротивления

2. Прямое КЗчетырёхполюсника (рис. 1, Кл. замкнут).

Z₂ = 0 и 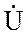₂ = 0.

Тогда уравнения (1) и (2) принимают вид:

_1к = A_{12 к},

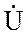
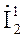
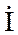
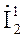
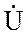
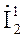
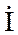
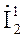
_1к = A_{22 к},

A₁₂ = _1к / _к; (6)

A₂₂ = _1к/ _к. (7)

По (5) и (7) находятся коэффициенты четырёхполюсника постоянного тока. Таким образом, для четырёхполюсника постоянного тока достаточно двух опытов, чтобы получить систему формул (1) и (2). Для четырёхполюсника переменного тока по проведенному опыту определяется Z_1K, а его связь с коэффициентами:

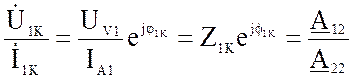
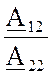
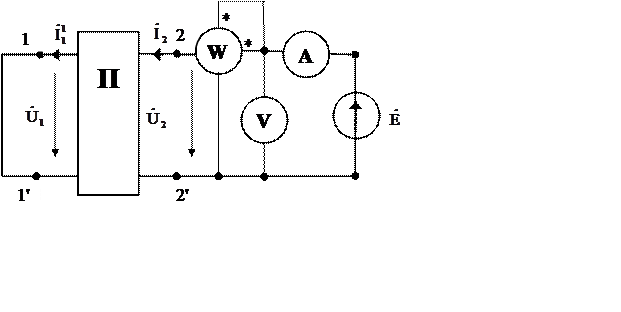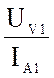
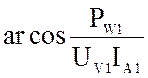
Z_1K = или Z_1K = (8)

Z_1K = и j_1K = модуль и аргумент входного сопротивления в режиме прямого КЗ

3. Обратное КЗ четырёхполюсника(рис. 2).

Система уравнений четырёхполюсника при его питании со стороны выходных зажимов:

₁ = A_{11 2} + A₁₂(−₂), (7)

− = A_{21 2} + A₂₂ (−₂). (8)

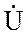
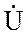
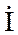
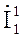
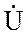
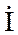
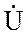
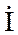
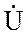
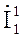
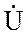
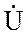
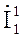
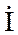
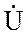
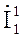
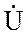
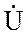
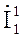
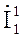
Выражая ₂ и ₂ через ₁ и _, в (7) и (8) получим:

₂ = A_{22 1} + A₁₂ ,

₂ = A_{21 1} + A₁₁ .

₁ = 0 и _2K = A_{12 K} I_2к = A_11K.

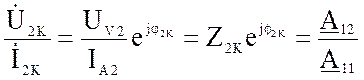
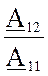
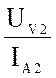
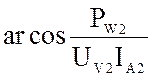
Z_2K = ; откуда Z_2K = . (9)

Z_2K = и j_2K = модуль и аргумент входного сопротивления в режиме обратного КЗ

Решая уравнения (5), (8) и (9) с учётом уравнения связи:

получаем формулы для определения коэффициентов:

A₁₁ =

A₂₁ =

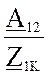
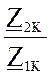
A₂₂ = = A₁₁ .

Источник

Четырехполюсники

Основные определения и классификация

Теория четырехполюсников используется в случае, когда интересуются взаимосвязью его входных и выходных величин и не рассматривают напряжения и токи внутри самого четырехполюсника. В развитии теории четырехполюсников принимали участие как зарубежные, так и отечественные ученые.

Часто заменяют один четырехполюсник другим, но эквивалентным. Под эквивалентностью двух четырехполюсников понимают возможность замены одного из них другим без изменения напряжений и токов в той цепи, к которой они подключаются.

Системы основных уравнений четырехполюсника

В первую очередь рассмотрим вариант в). Учитывая, что напряжения U1 и U2 могут быть заменены на ЭДС, на основании метода контурных токов могут быть записаны следующие уравнения

U1=I1Z11+Z12;

U2=I1Z21+Z22.

Уравнения (1) являются основными уравнениями четырехполюсника в форме |Z|. Здесь

— входное сопротивление со стороны первичных зажимов при разомкнутых вторичных;

— входное сопротивление со стороны вторичных зажимов при разомкнутых первичных;

.

Если уравнения (1) решить относительно токов I1 и , то получим основные уравнения четырехполюсника в форме |Y|

I1=U1Y11+U2Y12;

=U1Y21+U2Y22,

Достаточно широкое распространение, особенно в промэлектронике, получили уравнения в форме |Н| (гибридная форма), которая получается из системы (1), если её решить относительно U1 и

U1=I1H11+U2H12;

=I1H21+U2H22.

Чаще всего на практике используются основные уравнения в форме А. При питании четырехполюсника только со стороны первичных зажимов они имеют вид

U1=АU2+ВI2;

Входящие в уравнения (4) коэффициенты A, B, C, D характеризуют сам четырехполюсник и называются его коэффициентами. Они зависят от схемы четырехполюсника, от значений параметров его элементов и от частоты. Коэффициенты взаимосвязаны таким соотношением: AD—BC=1.

При питании четырехполюсника только со стороны вторичных зажимов основные уравнения принимают вид

U2=DU1+В;

=CU1+А.

Если четырехполюсник симметричный, то при перемене местами первичных и вторичных зажимов не изменяются напряжения и токи, поэтому для них, как следует из уравнений (4) и (5), А=D.

Опытное определение коэффициентов четырехполюсника

Коэффициенты A, B, C, D могут быть определены расчетным или опытным путем. Так как они взаимосвязаны, то для их определения необходимо еще 3 уравнения, для составления которых достаточно выполнить три опыта. Набор опытов может быть различным, но чаще всего используют следующий: холостой ход (ХХ) и короткое замыкание (КЗ) при питании со стороны первичных зажимов, а также опыт обратного КЗ, когда питание происходит со стороны вторичных зажимов. Первые два опыта выполняются по схеме рис.5.3,а, последний же по схеме рис.5.3,б. В каждом опыте по показаниям приборов определяются комплексы входных сопротивлений Z1х=Z1хejφ1х, Z1к=Z1кejφ1к и Z2к=Z2кejφ2к на основании следующих формул:

Z=U/I; r=P/I2; .

Для определения знака tgφ и φ необходимо либо включить фазометр, который показывает величину и знак угла φ, либо произвести дополнительный опыт. Для выполнения дополнительного опыта используют реактивный элемент (индуктивность или ёмкость), сопротивление которого примерно равна и который включают либо параллельно, либо последовательно с четырехполюсником, а по характеру изменения тока определяют знак φ.

Рассмотрим, как по известным Z1х=Z1хejφ1х, Z1к=Z1кejφ1к и Z2к=Z2кejφ2к, определить коэффициенты четырехполюсника. Свяжем входные сопротивления с коэффициентами. Для опыта ХХ (I2=0) уравнения (4) принимают вид: U1х=AU2х; I1х=CU2х. Поделив одно на другое, получаем

. (6)

Для опыта прямого КЗ (U2=0) уравнения (4) принимают вид: U1к=BI2к; I1к=DI2к. Поделив одно на другое, получаем

. (7)

Для опыта обратного КЗ (U1=0) уравнения (5) принимают вид: U2к=B; =А. Поделив одно на другое, получаем

. (8)

Схемы замещения четырехполюсника

.

Сравнивая полученное выражение со вторым уравнением системы (4), получаем

.

Сравнивая это выражение с первым уравнением системы (4), получаем

.

Из этих формул получаются следующие выражения для расчета сопротивлений Т-образной схемы замещения любого четырехполюсника

.

Аналогично для П-образной схемы

Из этих формул получаются следующие выражения для расчета сопротивлений П-образной схемы замещения любого четырехполюсника

Следует заметить, что бывают случаи, когда одна из рассмотренных схем замещения может оказаться физически нереализуемой.

Типы задач по четырехполюсникам

.

Затем определяем I1=U1/Z1 и задача сведена к первому типу.

Цепи с распределенными параметрами

До сих пор мы изучали цепи с сосредоточенными параметрами, т. е. такие, которые состоят из самостоятельно существующих R, L и С, расположенных в определенных точках цепи. Причем напряжения и токи в этих элементах мы связывали формулами ur=ir; uL=Ldi/dt; iC= CduC/dt, которые справедливы при том предположении, что ток, входящий в элемент равен току, выходящему из него. Однако представление электротехнических устройств в виде цепей с сосредоточенными параметрами не всегда возможно. Например, высоковольтная линия электропередачи (ЛЭП). Напомним, что в простейшем случае ЛЭП состоит из двух проводов, которые изолированы друг о друга и по которым собственно и передается электрическая энергия. В природе однако не существует идеальной изоляции, т. е. изоляции, обладающей бесконечно большим сопротивлением. Реальная изоляция имеет хотя и большое, но все же конечное значение сопротивления. В результате по такой изоляции начинает замыкаться ток, получивший название тока утечки. Если рабочее напряжение в линии высокое, то ток утечки достигает ощутимых значений. К чему приводит наличие тока утечки? Прежде всего к тому, что ток в различных местах линии становится неодинаковым, он непрерывно изменяется при переходе от одной точки линии к другой. И уж конечно нельзя утверждать, что ток в конце линии равен току на ее входе, как необходимо для цепи с сосредоточенными параметрами. Изменяется в линии и напряжение при переходе от одной точки к другой. Это происходит потому, что провода линии обладают активным и индуктивным сопротивлением. Рассмотрев данный пример, можно записать следующее определение: цепью с распределенными параметрами называется такая, у которой напряжение и ток непрерывно изменяются при переходе от одной точки к другой.

Кроме высоковольтных ЛЭП цепями с распределенными параметрами являются телефонные и телеграфные воздушные и кабельные линии связи. Цепями с распредпараметрами являются абсолютно все устройства, работающие на высоких частотах (антенные и фидерные устройства и т. д.). Строго говоря цепью с распредпараметрами следовало бы считать обычную катушку индуктивности. Действительно, индуктивность представляет собой катушку как правило цилиндрической формы, содержащую большое число витков медного или алюминиевого провода. Но между каждыми, рядом расположенными витками, имеется так называемая межвитковая емкость. Имеется емкость между каждым витком и землей (или корпусом катушки). Конечно эти емкости невелики, но они существуют. В связи с этим весь ток, замыкающийся по катушке условно может быть разбит на две части, одна из которых iL замыкается непосредственно по виткам катушки, а другая iC – по емкостям. Соотношение между этими частями может быть различным и в первую очередь оно зависит от частоты. При низких частотах, а низкими принято называть частоты до 1кГц, ток iC настолько мал, что им обычно пренебрегают. При повышении частоты картина изменяется поскольку индуктивное сопротивление прямо пропорционально частоте, а емкостное обратно пропорционально ей. Это приводит к тому, что при очень высоких частотах (109 ¸1011 Гц) ток iC становится большим тока iL и устройство следует считать уже обладающим емкостным сопротивлением. При промежуточных частотах (106 ¸ 108 Гц) токи iL и iC сравнимы друг с другом, пренебрегать нельзя ни тем ни другим, а, следовательно, катушка является цепью с распределенными параметрами. В связи с этим цепями с распредпараметрами считают обмотки высоковольтных электрических машин и трансформаторов.

Цепи с распредпараметрами делятся на линейные и нелинейные. Мы бодем изучать только линейные цепи, причем на конкретном примере высоковольтных ЛЭП, о которых поговорим чуть подробнее. В таких ЛЭП эффект непрерывного изменения напряжений и токов имеет место потому, что они обладают продольным и поперечным сопротивлениями. Продольное сопротивление образовано активным и индуктивным сопротивлениями самих проводов линии. Поперечное сопротивление представлено сопротивлением несовершенной изоляции и сопротивалением емкости между проводами. Ознакомившись с этими понятиями, можно записать еще одно определение: линия с распредпараметрами называется однородной, если продольное и поперечное сопротивления равномерно распределены по ее длине. В реальных линиях это не совсем так (из-за утечки тока в основном через гирлянды изоляторов, провеса проводов и т. д.), но с достаточно высокой степенью точности их можно считать однородными. Мы будем изучать именно однородные линии с распредпараметрами.

Основные дифуравнения однородной длинной линии

Линии с распредпараметрами часто называют длинными линиями. Произведем вывод уравнений, описывающих процессы, происходящие в них. При этом будем полагать, что известны первичные параметры линии, к числу которых относятся :

· r0 – активное сопротивление прямого и обратного проводов линии длиной 1 км;

· L0 – индуктивность петли, образованной прямым и обратным проводом линии длиной 1 км;

· g0 – проводимость изоляции между прямым и обратным проводами линии длиной 1 км;

· С0 – емкость между прямым и обратным поводом линии длиной 1 км.

Эти параметры могут быть либо раcсчитаны либо определены экспериментальным путем как будет показано ниже. 3

На основании второго закона Кирхгофа для контура, образованного рассматриваемым участком, имеем

По первому закону Кирхгофа

Если пренебречь величинами второго порядка малости, то получим

(2)

Уравнения (1) и (2) являются основными дифуравнениями однородной длинной линии. Они описывают как установившиеся режимы, так и переходные процессы. В математическом отношении решение этих уравнений в общем случае является весьма не простой задачей, но оно позволяет определить напряжение и ток в любой точке линии и в любой момент времени.

Установившийся режим в длинной линии при синусоидальном напряжении

Тогда величины, входящие в уравнения (1) и (2), принимают вид:

поскольку U зависит только от x и частная производная по x совпадает с полной производной.

, поскольку I от t не зависит.

, поскольку I также зависит только от x.

, поскольку U от t также не зависит.

Подставляя эти значения в уравнения (1) и (2), имеем:

или

где

Разделив переменные в двух последних дифуравнениях, получим:

Это линейное дифуравнение второго порядка, решение которого имеет вид:

В ТОЭ условились считать р1=-g, а р2=g, где

— (5)

это весьма важный параметр линии, который называется коэффициентом распространения. Он является комплексным числом g=a+b, причем a называется коэффициентом затухания и измеряется в Неперах (Нп) на километр, а b называется коэффициентом фазы и измеряется в рад/км.

(6)

Ток в рассматриваемой точке линии определится из выражения

, (7)

.

ZC называется характеристическим (волновым) сопротивлением и в общем случае оно является комплексным числом. Действительно

(8)

g, a, b и ZC характеризуют саму линию и называются ее вторичными параметрами.

Входящие в уравнения (6) и (7) постоянные интегрирования определяются по граничным условиям (значениям U и I в какой-либо точке линии). Если известны напряжение U1 и ток I1 в начале линии, т. е. при x=0. В этом случае уравнения (6) и (7) принимают вид

совместное решение которых дает:

и

Подставив их значения в формулы (6) и (7) и проделав несложные преобразования, получим

(9)

(10)

Формулы (9) и (10) являются основными уравнениями длинной линии в гиперболических функциях по U1, I1.

На практике однако чаще всего известны напряжение U2 и ток I2 в конце линии, т. е. при x=l, где l – длина линии. Подставив эти значения в формулы (6) и (7), получим:

, совместное решение которых дает

и

Если эти значения А1 и А2 подставить в (6) и (7) и собрать слагаемые, содержащие U2, а так же I2, то получим

(11)

(12)

Формулы (11) и (12) являются основными уравнениями длинной линии в гиперболических функциях по U2, I2.

Бегущие волны в линиях

Проясним физическую сущность процессов, происходящих в длинных линиях при передаче энергии при синусоидальных напряжениях и токах. Исходить при этом будем из уравнений (6) и (7), но учтем, что все величины, входящие в эти формулы, являются комплексами.

.

Перейдем от комплексов к мгновенным значениям

Как следует из этих выражений напряжение представляет собой сумму, а ток – разность двух синусоид, являющихся функцией двух переменных – времени t и координаты x. Первые составляющие представляют собой напряжение и ток падающей волны. Чтобы в этом убедиться изобразим график распределения вдоль линии (от x) первой составляющей, например, напряжения, предположительно являющейся падающей волной, в некоторый фиксированный момент времени t1 (рис.5.6)

и в момент времени t1+dt

где dx=vdt, а – это скорость движения волны вдоль линии.

Из этих выражений следует, что с ростом t uпад перемещается в сторону больших х, т. е. от начала линии к ее концу.

Падающей электромагнитной волной называется процесс перемещения волны от начала линии к её концу. Она состоит из волны напряжения, волны тока и несет энергию от приемника к источнику.

Аналогично можно показать, что вторые составляющие напряжения и тока представляют собой напряжение и ток отраженной волны. Убедимся в этом, построив график распределения второй составляющей напряжения вдоль линии (только от x) в моменты времени t=t1 и t=t1+dt (рис.5.7)

Отраженной электромагнитной волной называется процесс перемещения волны от конца линии к началу. Она состоит из волны напряжения и волны и несет энергию от приемника к источнику.

Падающие и отраженные волны, взятые вместе, называются бегущими волнами. Основными характеристиками бегущих волн являются фазовая скорость и длина волны. Фазовой скоростью v принято называть скорость перемещения неизменного фазового состояния. Для вывода формулы расчета v возьмем фазу допустим падающей волны, которая с ростом t должна оставаться неизменной w t + y1 — bx = const. Взяв производную по t, получим

. (13)

Длиной волны l называется наименьшее расстояние, взятое в направлении распространения волны, фаза колебания которых отличается на 2p, т. е.

откуда . (14)

Представляет интерес взаимосвязь между v и l

.

Бегущие волны по мере их продвижения по линии затухают и степень их затухания определяется величиной коэффициента a. С физической точки зрения затухание объясняется потерями энергии в активных элементах (r0, g0) линии.

Подводя итог, можно отметить, что

Из последних выражений следует закон Ома для падающих и отраженных волн

Входное сопротивление длинной линии

При расчете и анализе линий с распределенными параметрами широко используется её входное сопротивление, под которым понимают такое сосредоточенное сопротивление, которым в установившемся режиме можно заменить всю линию вместе с её нагрузкой и которое равно . Свяжем Z1 с параметрами линии. С этой целью запишем формулы (11) и (12) для начала линии (y=l) Тогда

, (15)

поскольку — это сопротивление нагрузки линии.

Особый интерес представляет входное сопротивление линии в режимах холостого хода (ХХ) и короткого замыкания (КЗ).

При ХХ (Z2 = ¥) I2 = 0 и уравнения (11) и (12), записанные для начала линии, принимают вид

(16)

При КЗ (Z2 = 0) U2 = 0 и уравнения (11) и (12), записанные для начала линии, принимают вид

. (17)

Зная Z1х и Z1к, которые могут быть определены экспериментальным путем, можно определить Z1 при любом сопротивлении Z2. Действительно

(18)

Осуществив опыты ХХ и КЗ, можно определить все параметры линии: как вторичные, так и первичные, а именно

или (19)

(20)

с другой стороны

тогда

где n – число длин волн, укладывающихся на длине линии.

Первичные параметры определяются по вторичным параметрам:

откуда

откуда .

Линия, согласованная с нагрузкой

Это означает, что в такой линии не возникает отраженная волна. По этой причине на практике стараются линию с нагрузкой согласовать.

Подставив эти значения в формулы (6) и (7), получим

. (21)

Формулы (21) являются основными уравнениями линии, согласованной с нагрузкой, они значительно более простые, чем формулы (11) и (12).

Формулы (21), записанные для начала линии, дают:

Тогда входное сопротивление линии

(22)

Из соотношения (22) следует, что, во-первых, Z1 не зависит от длины линии и, во вторых, что характеристическое сопротивление линии – это входное сопротивление линии, согласованной с нагрузкой, или входное сопротивление бесконечно длинной линии, в которой также не может возникнуть отраженная волна.

Определим КПД линии, согласованной с нагрузкой где Тогда

(23)

Как следует из (23) отличие между Р1 и Р2 определяется величиной al, которая называется затуханием линии и измеряется в Нп. Это условная единица измерения затухания. Последнее будет равняться 1Нп, если В связи широко используется другая единица измерения затухания – децибелл (1дБ=0.115Нп).

Линия без искажений

В ряде случаев к линии предъявляется требование, чтобы передаваемые по ней сигналы не искажались. Это особенно важно для линий связи (телефонных, телеграфных, радиорелейных и т. д.). Особенно ощутимы искажения при передаче музыки. Линия, которая не искажает сигналы и называется линией без искажений. Для того, чтобы передаваемые сигналы не искажались, необходимо выполнить два условия: а) все частоты, образующие сигнал, должны затухать в одинаковой степени, т. е. коэффициент затухания не должен зависеть от частоты; б) все частоты, образующие сигнал, должны распространяться с одинаковой скоростью, т. е. фазовая скорость не должна зависеть от частоты. Если не будет выполняться первое условие, то в линии имеют место амплитудные искажения, при невыполнении второго условия – фазовые искажения.

Известный ученый Хевисайд показал, что для того, чтобы линия не искажала передаваемые сигналы, её первичные параметры должны находиться во вполне определенном соотношении, а именно:

(24)

Убедимся в том, что при выполнении условия (24), искажений в линии не будет. С этой целью определим вторичные параметры линии

Отсюда (25)

(26)

(27)

(28)

Из (25) и (27) следует, что условия неискажающей передачи сигналов выполняются (a и v не зависят от частоты), а из (28) следует, что у такой линии ZC является чисто активным ( в ряде случаев это очень ценно). Кроме того линия без искажений обладает минимальным значением a при заданных r0 и g0, а, следовательно, максимальным значением КПД, определяемым при согласованной нагрузке по (23).

Часто при высоких частотах имеет место соотношение r0

Источник