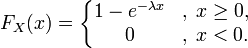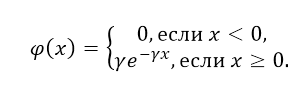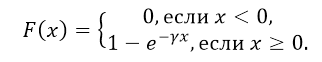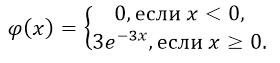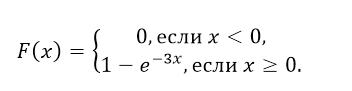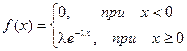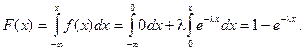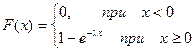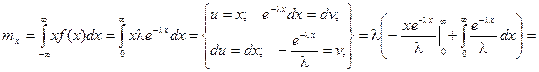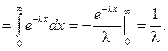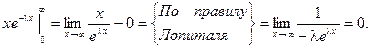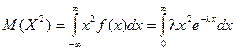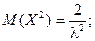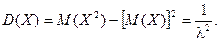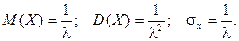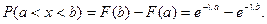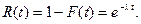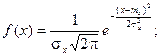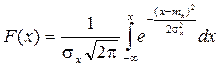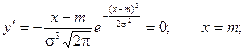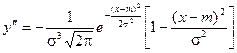сколько параметров имеет показательное распределение
Показательное распределение
Показательное распределение
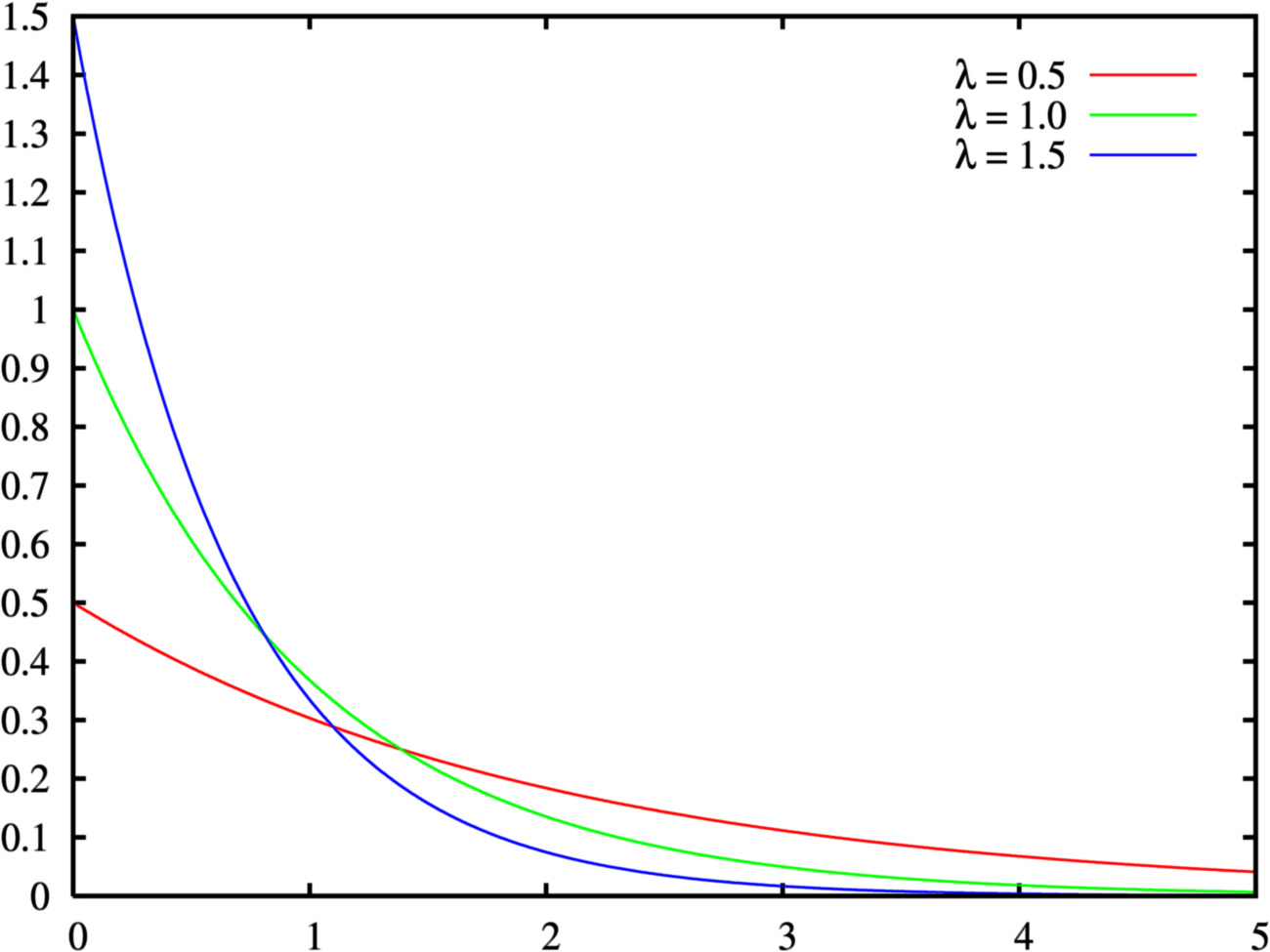
Плотность вероятности  | |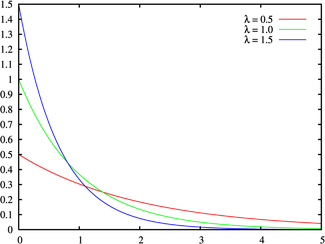
Функция распределения  | |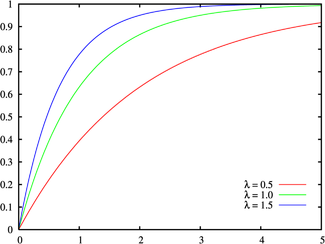
| Параметры | 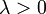 — интенсивность или обратный коэффициент масштаба |
| Носитель |  |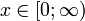
| Плотность вероятности |  |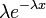
| Функция распределения |  |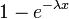
| Математическое ожидание |  |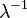
| Медиана |  |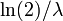
| Мода |  |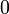
| Дисперсия |  |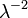
| Коэффициент асимметрии |  |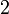
| Коэффициент эксцесса |  |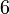
| Информационная энтропия |  |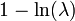
| Производящая функция моментов |  |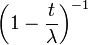
| Характеристическая функция |  |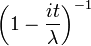
Показательное распределение — абсолютно непрерывное распределение, моделирующее время между двумя последовательными свершениями одного и того же события.
Содержание
Определение
.
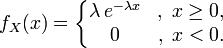
Иногда семейство экспоненциальных распределений параметризуют обратным параметром 1 / λ :
.
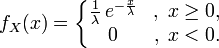
Оба способа одинаково естественны, и необходима лишь договорённость, какой из них используется.
В этой статье для определённости будем предполагать, что плотность экспоненциальной случайной величины X задана первым уравнением, и будем писать: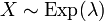 
.
Функция распределения
Моменты
Несложным интегрированием находим, что производящая функция моментов для экспоненциального распределения имеет вид:
,
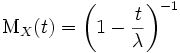
откуда получаем все моменты:
.
, 
.
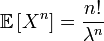
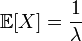
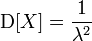
Отсутствие памяти
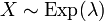
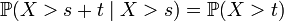
Пусть . Тогда 
.
Пример. Пусть автобусы приходят на остановку случайно, но с некоторой фиксированной средней интенсивностью. Тогда количество времени, уже затраченное пассажиром на ожидание автобуса, не влияет на время, которое ему ещё придётся прождать.
Связь с другими распределениями
| править | |||||||||||
Полезное
Смотреть что такое «Показательное распределение» в других словарях:
показательное распределение — экспоненциальное распределение — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы экспоненциальное распределение EN exponential distribution … Справочник технического переводчика
Показательное распределение — распределение вероятностей на действительной прямой с плотностью вероятностей (См. Плотность вероятности) р (х), равной при х ≥ 0 показательной функции λe λx, λ > 0 [отсюда название П. р.] и при х … Большая советская энциклопедия
ОТРИЦАТЕЛЬНОЕ ПОКАЗАТЕЛЬНОЕ РАСПРЕДЕЛЕНИЕ — то же, что показательное распределение … Математическая энциклопедия
РАСПРЕДЕЛЕНИЕ ВЕРОЯТНОСТЕЙ — одно из основных понятий вероятностей теории и математической статистики. При современном подходе в качестве математич. модели изучаемого случайного явления берется соответствующее вероятностное пространство
Экспоненциальное распределение — Показательное распределение Плотность вероятности Функция распределения … Википедия
НЕПРЕРЫВНОЕ РАСПРЕДЕЛЕНИЕ — распределение вероятностей, не имеющее атомов. Если атомы суть отдельные точки, то Н. р. противоположно дискретному распределению (см. также Атомическое распределение). Вместе с дискретным распределением Н. р. образует основные типы распределений … Математическая энциклопедия
ЭРЛАНГА РАСПРЕДЕЛЕНИЕ — эрланговское распределение, сосредоточенное на распределение вероятностей с плотностью где целое и действительное параметры. Характеристич. функция Э. р. имеет вид а математич. ожидание и дисперсия соответственно и … Математическая энциклопедия
ЛАПЛАСА РАСПРЕДЕЛЕНИЕ — непрерывное распределение вероятностей с плотностью где параметр сдвига, а a>0, масштабный параметр. Плотность Л. р. симметрична относительно точки x=b, производная плотности имеет разрыв при x=b. Характеристич. функция Л. р. с параметрами a и … Математическая энциклопедия
ЭКСПОНЕНЦИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ — то же, что показательное распределение … Математическая энциклопедия
Экспоненциальное распределение
Oct 10, 2019 · 6 min read
Мы всегда начинаем с вопроса “почему”, прежде чем переходить к формулам. Если вы понимаете, почему что-то работает, вы с большей вероятностью будете применять это в своей работе.
1. Почему мы изобрели экспоненциальное распределение?
Ответ: чтобы получить распределение, предсказывающее периоды времени между событиями (такими как успех, отказ, доставка и так далее).
Например, мы хотим предсказать следующее:
Следующий вопрос такой: почему λ * e^(−λt) — это плотность вероятности времени до следующего события?
И следующий вопрос: что значит X
EXP(0,25)? Параметр 0,25 означает 0,25 минут, часов или дней, а, может, 0,25 событий?
Предполагается, что вы хорошо знакомы с распределением Пуассона. Если нет, эта статья поможет разобраться.
EX P (λ) ➡ Э кспоненциальный параметр λ тот же самый, что и λ в распределении Пуассона?
Важная вещь, которая позже поможет вам не запутаться с X
EXP(0,25). 0,25 — это не временной период, а число событий, совпадающее с параметром λ в процессе Пуассона.
Например, ваш блог посещают 500 пользователей в день. Это среднее значение. Количество клиентов магазина за час, землетрясений в год, автомобильных аварий в неделю, опечаток на странице и так далее — это средние значения событий (λ) в единицу времени, являющиеся параметром распределения Пуассона.
Однако при моделировании времени между событиями удобнее использовать термины времени, а не количества. Например, число лет, в течение которых компьютер может включаться без ошибок — 10 лет (это удобнее, чем говорить “ 0,1 ошибка в год”), новый покупатель приходит каждые 10 минут, крупные ураганы возникают каждые 7 лет и так далее.
Путаница возникает, когда вы видите термин “ затухание”, или еще хуже, “ скорость затухания”, которые часто используются в экспоненциальном распределении. З атухание выражается через время (каждые 10 минут, каждые 7 лет и т.д.) и является обратной величиной параметра (λ) в распределении Пуассона. Смотрите: если у вас 3 посетителя в час, значит у вас 1 посетитель каждую треть часа.
Итак, мы можем ответить на вопрос:
Что значит “X
Это означает, что параметр Пуассона будет равен 0,25. В течение единицы времени (неважно, в минутах, часах или годах) событие происходит в среднем 0,25 раз. Переводя в термины времени — пройдет 4 часа, прежде чем событие произойдет, если за единицу времени принят 1 час.
2. Вывод плотности вероятности
Наш первый вопрос был: почему λ * e^(−λt) — это плотность вероятности времени до следующего события?
Определение экспоненциального распределения — это распределение вероятности времени *между* событиями в процессе Пуассона.
Смотрите: в период ожидания не происходит ни одного события. Другими словами, Пуассон (X=0).
Есть важная вещь, которую стоит помнить о пуассоновской плотности вероятности: период времени, в течение которого возникают пуассоновские события (X=k), составляет только одну (1) единицу времени.
Как смоделировать распределение вероятности не просто в течение одной единицы времени, а “ ничего не произошло в период времени t”?
Распределение Пуассона предполагает, что события возникают независимо друг от друга. Следовательно, можно посчитать вероятность нулевого успеха в течение t единиц времени, умножив P(X=0 в единицу времени) на t раз.
Плотность вероятности — это производная от кумулятивной функции распределения вероятности.
Поскольку у нас уже есть кумулятивная функция распределения вероятности экспоненциального распределения, 1 — P(T > t), мы можем получить плотность вероятности, продифференцировав ее.
Показательное распределение
Вы будете перенаправлены на Автор24
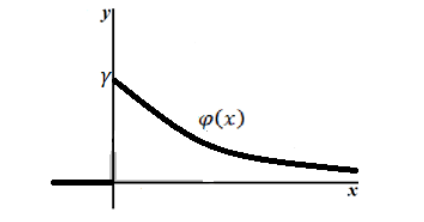
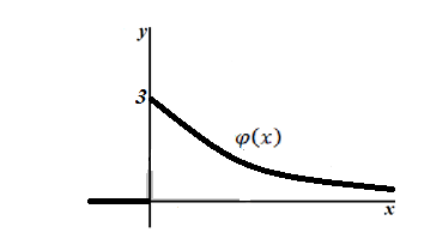
График плотности показательного распределения имеет вид (рис. 1):
Рисунок 2. График плотности показательного распределения.
Функция показательного распределения
Как нетрудно проверить, функция показательного распределения имеет вид:
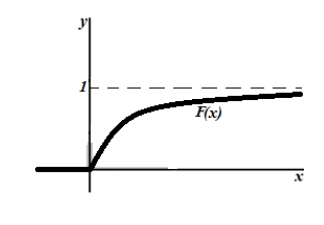
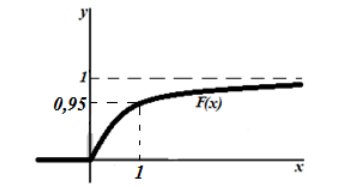
График функции показательного распределения имеет вид:
Рисунок 4. График функции показательного распределения.
Вероятность попадания случайной величины при показательном распределении
Пример задачи на показательное распределение
Найти плотность распределения и построить её график.
Найти функцию распределения и построить её график.
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение данного распределения.
Показательное распределение
Определение. Показательным (экспоненциальным)называется распределение вероятностей непрерывной случайной величины Х, которое описывается плотностью
Найдем закон распределения.
Графики функции распределения и плотности распределения:
f(x) F(x)
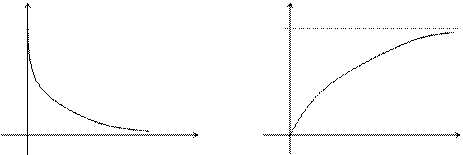
Найдем математическое ожидание случайной величины, подчиненной показательному распределению.
Результат получен с использованием того факта, что
Для нахождения дисперсии найдем величину М(Х 2 ).
Дважды интегрируя по частям, аналогично рассмотренному случаю, получим:
Тогда 
Итого: Видно, что в случае показательного распределения математическое ожидание и среднее квадратическое отклонение равны.
Также легко определить и вероятность попадания случайной величины, подчиненной показательному закону распределения, в заданный интервал.
Показательное распределение широко используется в теории надежности.
Допустим, некоторое устройство начинает работать в момент времени t0=0, а через какое – то время t происходит отказ устройства.
Обозначим Т непрерывную случайную величину – длительность безотказной работы устройства.
Таким образом, функция распределения F(t) = P(T t) = 1 – F(t).
Определение. Функцией надежности R(t) называют функцию, определяющую вероятность безотказной работы устройства в течение времени t.
Часто на практике длительность безотказной работы подчиняется показательному закону распределению.
Вообще говоря, если рассматривать новое устройство, то вероятность отказа в начале его функционирования будет больше, затем количество отказов снизится и будет некоторое время иметь практически одно и то же значение. Затем (когда устройство выработает свой ресурс) количество отказов будет возрастать.
Другими словами, можно сказать, что функционирование устройства на протяжении всего существования (в смысле количества отказов) можно описать комбинацией двух показательных законов (в начале и конце функционирования) и равномерного закона распределения.
Функция надежности для какого- либо устройства при показательном законе распределения равна:
Данное соотношение называют показательным законом надежности.
Важным свойством, позволяющим значительно упростить решение задач теории надежности, является то, что вероятность безотказной работы устройства на интервале времени t не зависит от времени предшествующей работы до начала рассматриваемого интервала, а зависит только от длительности времени t.
Таким образом, безотказная работа устройства зависит только от интенсивности отказов l и не зависит от безотказной работы устройства в прошлом.
Так как подобным свойством обладает только показательный закон распределения, то этот факт позволяет определить, является ли закон распределения случайной величины показательным или нет.
2.8 Распределение «Хи-квадрат»
распределена по закону 
(«Хи-квадрат») с k=n степенями свободы; если же эти величины связаны одним линейным соотношением, например 
, то число степеней свободы k=n-1.
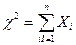
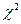
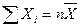
Плотность этого распределения
где 
-Гамма-функция; в частности,
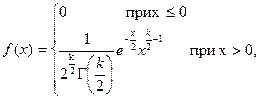
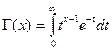
Отсюда видно, что распределение «Хи-квадрат» определяется одним параметром – числом степеней свободы k. С увеличением числа степеней свободы распределение медленно приближается к нормальному.
2.9 Распределение Стьюдента
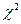
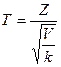
Пусть Z –нормальная случайная величина, причем M(Z)=0, s(Z)=1, а V- независимая от Z величина, которая распределена по закону с k степенями свободы. Тогда величина
имеет распределение, которое называют t- распределением или распределением Стьюдента, k степенями свободы. Итак отношение нормированной нормальной величины к квадратному корню из независимой случайной величины, распределенной по закону
2.9 Нормальный закон распределения
Определение. Нормальнымназывается распределение вероятностей непрерывной случайной величины, которое описывается плотностью вероятности
Нормальный закон распределения также называется законом Гаусса.
Нормальный закон распределения занимает центральное место в теории вероятностей. Это обусловлено тем, что этот закон проявляется во всех случаях, когда случайная величина является результатом действия большого числа различных факторов. К нормальному закону приближаются все остальные законы распределения.
Можно легко показать, что параметры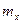 
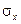
и 
, входящие в плотность распределения являются соответственно математическим ожиданием и средним квадратическим отклонением случайной величины Х.
Найдем функцию распределения F(x).
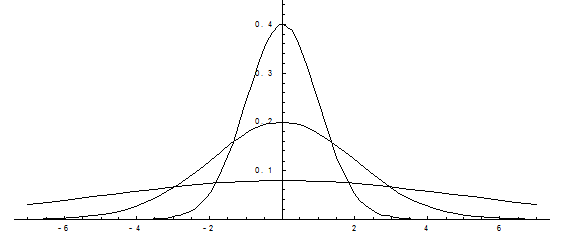
График плотности нормального распределения называется нормальной кривой или кривой Гаусса.
Нормальная кривая обладает следующими свойствами:
1) Функция определена на всей числовой оси.
2) При всех х функция распределения принимает только положительные значения.
3) Ось ОХ является горизонтальной асимптотой графика плотности вероятности, т.к. при неограниченном возрастании по абсолютной величине аргумента х, значение функции стремится к нулю.
4) Найдем экстремум функции.
5) Функция является симметричной относительно прямой х = а, т.к. разность
(х – а) входит в функцию плотности распределения в квадрате.
6) Для нахождения точек перегиба графика найдем вторую производную функции плотности.
В этих точках значение функции равно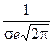 
.
Построим график функции плотности распределения.
Построены графики при т =0 и трех возможных значениях среднего квадратичного отклонения s = 1, s = 2 и s = 7. Как видно, при увеличении значения среднего квадратичного отклонения график становится более пологим, а максимальное значение уменьшается..
Если а > 0, то график сместится в положительном направлении, если а