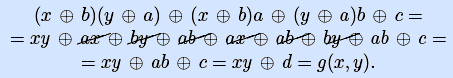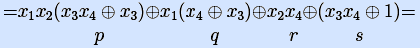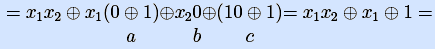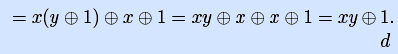что значит не умаляя общности
Рецензии на произведение «Вариации на тему Гёделя, или Тезисы Мата»
И снова математика.
Ещё в институте, на лекциях по Дискретной Математике( графы, Машина Тьюринга, Теория Чисел), мне «не нравились» аксиомы, вошедшие в эту дисциплину с лёгкой руки Джузеппе Пиано.
Так вот, одна из этих аксиом гласит:
На мой взгляд, теорема Гёделя о неполноте как раз и доказала правильность такого подхода к так называемым натуральным числам.
Лучше скажите — является ли математика инструментом познания окружающего мира, или она всего лишь заложница законов человеческой психики?
Портал Проза.ру предоставляет авторам возможность свободной публикации своих литературных произведений в сети Интернет на основании пользовательского договора. Все авторские права на произведения принадлежат авторам и охраняются законом. Перепечатка произведений возможна только с согласия его автора, к которому вы можете обратиться на его авторской странице. Ответственность за тексты произведений авторы несут самостоятельно на основании правил публикации и законодательства Российской Федерации. Данные пользователей обрабатываются на основании Политики обработки персональных данных. Вы также можете посмотреть более подробную информацию о портале и связаться с администрацией.
Ежедневная аудитория портала Проза.ру – порядка 100 тысяч посетителей, которые в общей сумме просматривают более полумиллиона страниц по данным счетчика посещаемости, который расположен справа от этого текста. В каждой графе указано по две цифры: количество просмотров и количество посетителей.
© Все права принадлежат авторам, 2000-2021. Портал работает под эгидой Российского союза писателей. 18+
Что значит не умаляя общности
Рассмотрим следующее разложение булевой функции f(x1, …, xn) по переменной xi.
Разложение Шеннона. f(x1, …, xn) = xi f(x1, …, xi-1,1,xi+1, …, xn) 
Доказательство (не умаляя общности, для i=1). При x1=0 имеем:
f(0,x2, …, xn)=0f(1,x2, …, xn) 
f(1,x2, …, xn)=1f(1,x2, …, xn) 
Следовательно, разложение верно. •
Определение. Сомножитель f(x1, …, xi-1,1,xi+1, …, xn) называется коэффициентом разложения функции f(x1, …, xn) по переменной xi при xi, а сомножитель f(x1, …, xi-1,0,xi+1, …, xn) – коэффициентом разложения функции f(x1, …, xn) по переменной xi при x i.
Пример. Булеву функцию f(x,y,z)= y 

[ упростим коэффициенты разложения на основе свойств 0 и 1 для конъюнкции ]
[ продолжим упрощение коэффициента при x на основе свойства 0 для эквивалентности a 
в результате имеем следующие коффициенты разложения, зависящие лишь от y и z:
y 

Что значит не умаляя общности
Пусть a, b, c – положительные числа, сумма которых равна 1. Докажите неравенство:
Решение 1
Заметим, что (мы использовали неравенство между средним арифметическим и средним гармоническим для положительных x, y). Осталось сложить три аналогичных неравенства.
Решение 2
Не умаляя общности, можно считать, что a ≥ b ≥ c, тогда 1 – c² ≥ 1 – b² ≥ 1 – a² и, следовательно,
Заметим, что Таким образом, нужно доказать неравенство
Поскольку сумма числителей равна 0, неравенство будет доказано, если мы заменим знаменатели на равные таким образом, что каждая дробь при этом не увеличится. Если a ≥ b ≥ ⅓ ≥ c, то заменим все знаменатели на 1 – c², в результате отрицательное слагаемое не изменится, а положительные не увеличатся. Если a ≥ ⅓ b ≥ c, то заменим все знаменатели на 1 – b², тогда положительное слагаемое и одно из отрицательных только уменьшатся, а второе отрицательное слагаемое останется неизменным.
Источники и прецеденты использования
| олимпиада | |
| Название | Всероссийская олимпиада по математике |
| год | |
| Год | 2003 |
| Этап | |
| Вариант | 5 |
| Класс | |
| Класс | 9 |
| задача | |
| Номер | 03.5.9.6 |
Что значит не умаляя общности
Определение. Булева функция называется линейной (принадлежит классу L), если ее полином Жегалкина линеен.
Примеры. Мажоритарная функция не является линейной: степень ее полинома Жегалкина (xy 

Доказательство. Полином Жегалкина линейной функции f(x1, …, xn) имеет вид:
Пример. Из всех 16 булевых функций двух аргументов x1, x2 8 функций (2 2+1 ) принадлежат классу L: 0, 1, 

Теорема о замкнутости класса L. Множество всех линейных булевых функций является замкнутым классом.
Доказательство. Рассмотрим суперпозицию любых булевых функций из L, то есть функцию
и покажем, что она является линейной. Представим каждую из функций, образующих суперпозицию, полиномом Жегалкина:
Подставив эти полиномы в суперпозицию, получим:
Поскольку в последней формуле каждая скобка есть булева константа, то получен линейный полином Жегалкина. Значит, функция f(x1, …, xn) линейная, и класс L замкнут. •
В первых трех группах вынесем за скобки соответственно x1x2, x1 и x2 :
где a, b, c – булевы константы.
Если a=b=c=0, конъюнкция получена. Иначе положим в последней формуле x1= x 



Если булева константа d=0, конъюнкция xy получена. Иначе функция g(x,y)= x y. Тогда, инвертировав исходную функцию (что допустимо по условию теоремы), получим конъюнкцию xy. •
Пример. Рассмотрим нелинейную булеву функцию, заданную полиномом Жегалкина.
[ выберем первую конъюнкцию x1x2 x3x4, в ней выберем переменные x1, x2 и сгруппируем конъюнкции ]
[ p(x3,x4)=1 при x3=1, x4=0, подставим эти значения переменных в формулу ]
[ положим x1=x 


Инвертировав исходную функцию, получим конъюнкцию xy. •
не уменьшая общности
1 without losing generality
2 without loss of generality
См. также в других словарях:
Теорема Декарта — или правило знаков Декарта, теорема, утверждающая, что число положительных корней многочлена с вещественными коэффициентами равно числу перемен знаков в ряду его коэффициентов или на чётное число меньше этого числа (корни считаются с учётом … Википедия
Регулярные тепловые режимы — Для того чтобы ввести понятие регулярного теплового режима, рассмотрим процесс охлаждения (нагрева) в среде с постоянной температурой произвольного по форме однородного и изотропного тела, начальное распределение температур в котором в начальный… … Википедия
Медицина — I Медицина Медицина система научных знаний и практической деятельности, целями которой являются укрепление и сохранение здоровья, продление жизни людей, предупреждение и лечение болезней человека. Для выполнения этих задач М. изучает строение и… … Медицинская энциклопедия
Комплекс неполноценности — 1. ключевой термин теории А.Адлера о движущих силах личностного развития, означает осознание своей общей несостоятельности, проявляющееся уходом от трудностей, избеганием проблем, решение которых требует серьёзных усилий, а также симптомами… … Энциклопедический словарь по психологии и педагогике
Менделе Мойхер Сфорим — [Mendele Mojcher Sforim, 1836 1917] Менделе Книгоноша, псевдоним Шолом Яков Абрамовича. Основоположник еврейской литературы, старейший классик. Род. в местечке Капулье (Белоруссия). До 17 лет учился в религиозных школах (ешиботах), свыше года… … Большая биографическая энциклопедия
Менделе-Мойхер-Сфорим — (Mendele Mojcher Sforim, 1836 1917) Менделе Книгоноша, псевдоним Шолом Яков Абрамовича. Основоположник еврейской литературы, старейший классик. Р. в местечке Капулье (Белоруссия). До 17 лет учился в религиозных школах (ешиботах), свыше года… … Литературная энциклопедия
Религии Африки — В Африке распространено несколько основных религий. Большинство африканцев придерживается христианства или ислама, однако многие их приверженцы также практикуют и традиционные африканские религии, включая народные и синкретические[1] … Википедия
расы — расы, человеческие группы, выделяемые на основании исторически возникшей общности наследственно обусловленных биологических особенностей. Расовый комплекс представляет собой мозаику признаков, возникших в разное время на разных территориях.… … Энциклопедия «Народы и религии мира»