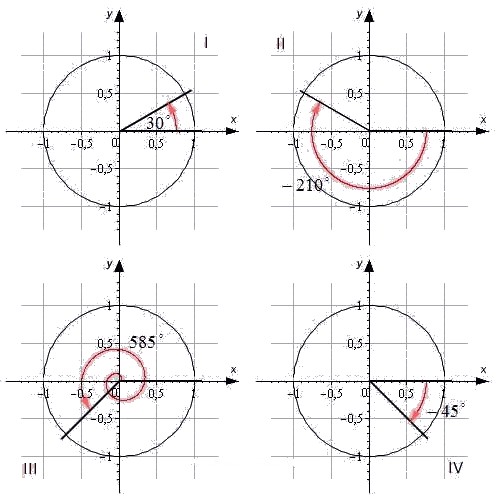
какие значения принимает синус
1.2.1 Синус, косинус, тангенс, котангенс произвольного угла
Видеоурок: Синус, косинус, тангенс и котангенс угла
Лекция: Синус, косинус, тангенс, котангенс произвольного угла

Синусом угла данной окружности, образованного радиусом-вектором ОР, является ордината точки Р вектора на окружности.
То есть, для получения значения синуса данного угла альфа необходимо определиться с координатой У на плоскости.
То есть, для получения значения косинуса данного угла альфа необходимо определиться с координатой Х на плоскости.
Тангенсом произвольного угла считается отношение синуса к косинусу.
Если рассматривать прямоугольный треугольник, то это отношение противолежащего катета к прилежащему. Если же речь идет о единичной окружности, то это отношение ординаты к абсциссе.
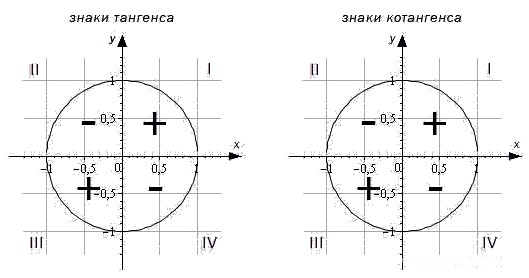
Судя по данным отношениям, можно понять, что тангенс не может существовать, если значение абсциссы равно нулю, то есть при угле в 90 градусов. Все остальные значения тангенс принимать может.
Тангенс имеет положительное значение в первой и третьей четверти единичной окружности, а во второй и четвертой является отрицательным.
Так как ордината находится в знаменателе дроби, то котангенс не может существовать при угле альфа, равном нулю градусов.
Котангенс принимает те же значения в четвертях единичной окружности, что и тангенс.
Все перечисленные функции являются периодичными. Косинус и синус имеют период 360 градусов, то есть 2Пи, а тангенс и котангенс 180 градусов, то есть Пи.
Синус, косинус, тангенс и котангенс: определения в тригонометрии, примеры, формулы
Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии.
Синус, косинус, тангенс и котангенс. Определения
Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.
Определения тригонометрических функций
Данные определения даны для острого угла прямоугольного треугольника!
В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.
Определения синуса, косинуса, тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.
Угол поворота
В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность с центром в начале декартовой системы координат.
Синус (sin) угла поворота
При решении практических примеров не говорят «синус угла поворота α «. Слова «угол поворота» просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.
Числа
Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?
Синус, косинус, тангенс, котангенс числа
Синусом, косинусом, тангенсом и котангенсом числа t называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в t радиан.
Например, синус числа 10 π равен синусу угла поворота величиной 10 π рад.
Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.
Любому действительному числу t ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.
Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.
Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу t, совпадает с точкой, в которую переходит начальная точка после поворота на угол t радиан.
Тригонометрические функции углового и числового аргумента
Основные функции тригонометрии
Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.
Связь определений sin, cos, tg и ctg из геометрии и тригонометрии
Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.
В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.
sin α = A 1 H O A 1 = y 1 = y
Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.
Основное тригонометрическое тождество
9 класс, 10 класс, ЕГЭ/ОГЭ
Связь между sin и cos одного угла
Вы уже наверняка знаете, что тождественный — это равный.
Основные тригонометрические тождества — это равенства, которые устанавливают связь между синусом, косинусом, тангенсом и котангенсом одного угла. Это значит, что любую из этих функций можно найти, если известна другая функция.
Ключ к сердцу тригонометрии — основное тригонометрическое тождество. Запомните и полюбите его, чтобы отношения с тригонометрией сложились самым наилучшим образом:
sin 2 α + cos 2 α = 1
Из основного тождества вытекают равенства тангенса и котангенса, поэтому оно — ключевое.
Равенство tg 2 α + 1 = 1/cos 2 α и равенство 1 + сtg 2 α + 1 = 1/sin 2 α выводят из основного тождества, разделив обе части на sin 2 α и cos 2 α.
В результате деления получаем:
Поэтому основному тригонометрическому тождеству уделяется максимум внимания. Но какая же «метрия» может обойтись без доказательств. Видите тождество — доказывайте, не раздумывая.
sin 2 α + cos 2 α = 1
Сумма квадратов синуса и косинуса одного угла тождественно равна единице.
Чтобы доказать тождество, обратимся к теме единичной окружности.
Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат. Радиус единичной окружности равен единице.
Докажем тождество sin 2 α + cos 2 α = 1
Образовался прямоугольный треугольник OA1B.
Основное тригонометрическое тождество связывает синус угла и косинус угла. Зная одно, вы легко можете найти другое. Нужно лишь извлечь квадратный корень по формулам:
Как видите, перед корнем может стоять и минус, и плюс. Основное тригонометрическое тождество не дает понять, положительным или отрицательным был исходный синус/косинус угла.
Как правило, в задачках с подобными формулами уже есть условия, которые помогают определиться со знаком. Обычно такое условие — указание на координатную четверть. Таким образом без труда можно определить, какой знак нам требуется.
Тангенс и котангенс через синус и косинус
Из всего этого множества красивых, но не сильно понятных слов, можно сделать вывод о зависимости одного от другого. Такая связь помогает отдельно преобразовывать нужные величины.
Исходя из определений:
Это позволяет сделать вывод, что тригонометрические тождества

задаются sin и cos углов.
Отсюда следует, что тангенс угла — это отношение синуса угла к косинусу. А котангенс угла — это отношение косинуса к синусу.
Отдельно стоит обратить внимание на то, что тригонометрические тождества

верны для всех углов α, значения которых вписываются в диапазон.
применимо для любого угла α, не равного π * z, где z — это любое целое число.
Связь между тангенсом и котангенсом
Уж насколько очевидной кажется связь между ранее рассмотренными тождествами, настолько еще более наглядна связь между тангенсом и котангенсом одного угла.
Такое тождество применимо и справедливо при любых углах α, значение которых не равняются π/2 * z, где z — это любое целое число. В противном случае, функции не будут определены.
Как и любое другое, данное тригонометрическое тождество подлежит доказательству. Доказывать его очень просто.
tg α * ctg α = 1.
Получается, что тангенс и котангенс одного угла, при котором они имеют смысл — это взаимно обратные числа.
Если числа a и b взаимно обратные — это значит, что число a — это число, обратное числу b, а число b — это число, обратное числу a. Кроме того, это значит, что числу a обратно число b, а числу b обратно число a. Короче, и так, и эдак.
Тангенс и косинус, котангенс и синус
Все тождества выше позволяют сделать вывод, что тангенс угла связан с косинусом угла, а котангенс угла — с синусом.
Эта связь становится очевидна, если взглянуть на тождества:
Сумма квадрата тангенса угла и единицы равна числу, обратному квадрату косинуса этого угла.
Сумма единицы и квадрата котангенса угла равна числу, обратному квадрату синуса этого угла.
Вывести оба этих тождества можно из основного тригонометрического тождества:
sin 2 α + cos 2 α = 1.
Хорошо бы выучить все формулы и запомнить формулировки тождеств наизусть. Чтобы это сделать, сохраняйте себе табличку с основными формулами.
Основные тригонометрические тождества
sin 2 α + cos 2 α = 1
tg 2 α + 1 =
1 + ctg 2 α =
Чтобы тратить еще меньше времени на решение задач, сохраняйте таблицу значений тригонометрических функции углов, которые чаще всего встречаются в задачах.
Примеры решения задач
Разберем пару задачек, для решения которых нужно знать основные тождества. Рассмотрите внимательно предложенные решения и потренируйтесь самостоятельно.
Задачка 1. Найдите cos α, tg α, ctg α при условии, что sin α = 12/13.
Задачка 2. Найдите значение cos α,
если:
Подставляем значения sin α:
Как видите, задачи решаются достаточно просто, нужно лишь верно применять формулы основных тождеств.
Тригонометрия простыми словами
Официальное объяснение тригонометрии вы можете почитать в учебниках или на других интернет сайтах, а в этой статье мы хотим объяснить суть тригонометрии «на пальцах».
Для удобства работы с тригонометрическими функциями был придуман тригонометрический круг, который представляет собой окружность с единичным радиусом (r = 1).
Тогда проекции радиуса на оси X и Y (OB и OA’) равны катетам построенного треугольника ОАВ, которые в свою очередь равны значениям синуса и косинуса данного угла.
Тангенс и котангенс получаются соответстсвенно из треугольников OCD и OC’D’, построенных подобно исходному треугольнику OAB.
Для упрощения обучения тригонометрическим функциям в школе используют только некоторые удобные углы в 0°, 30°, 45°, 60° и 90°.
Значения тригонометрических функций повторяются каждые 90° и в некоторых случаях меняя знак на отрицательный.
Достаточно запомнить значения некоторых важных углов и понять принцип повтора значений для бОльших углов.
Значения тригонометрических функций
для первой четверти круга (0° – 90°)
Принцип повтора знаков тригонометрических функций
Угол может быть как положительный, так и отрицательный. Отрицательный угол считается угол, откладываемый в противоположную сторону.
В виду того, что полная окружность составляет 360°, значения тригонометрических функций углов, описывающих одинаковое положение радиуса, РАВНЫ.
Для лучшего понимания и запоминания значений тригонометрических функций воспользуйтесь динамическим макетом тригонометрического круга ниже. Нажимая кнопки «+» и «–» значения угла будут увеличиваться или уменьшаться соответственно.
Тригонометрический круг
Углы в радианах
Чтобы закрепить свои знания и проверить себя, воспользуйтесь онлайн-тренажером для запоминания значений тригонометрических функций.
Свойства синуса, косинуса, тангенса и котангенса
В этой статье будут рассмотрены три основных свойства тригонометрических функций: синуса, косинуса, тангенса и котангенса.
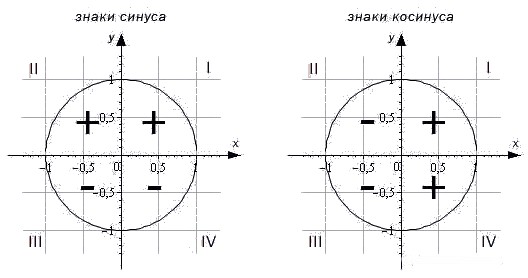
Знаки тригонометрических функций по четвертям
Часто в математическом тексте или в контексте задачи можно встретить фразу: «угол первой, второй, третьей или четвертой координатной четверти». Что это такое?
Для наглядности приведем иллюстрацию.
Теперь рассмотрим знаки, которые принимают синус, косинус, тангенс и котангенс в зависимости от того, в какой четверти лежит угол.
Свойство периодичности
При изменении угла на целое число полных оборотов значения синуса, косинуса, тангенса и котангенса данного угла остаются неизменными.
Действительно, при изменении угла на целое число оборотов мы всегда будем попадать из начальной точки A на единичной окружности в точку A 1 с одними и теми же координатами. Соответственно, не будут меняться и значения синуса, косинуса, тангенса и котангенса.
Математически данное свойство записывается так:
sin α + 2 π · z = sin α cos α + 2 π · z = cos α t g α + 2 π · z = t g α c t g α + 2 π · z = c t g α
Какое применение на практике находит это свойство? Свойство периодичности, как и формулы приведения, часто используется для вычисления значений синусов, косинусов, тангенсов и котангенсов больших углов.
sin 13 π 5 = sin 3 π 5 + 2 π = sin 3 π 5
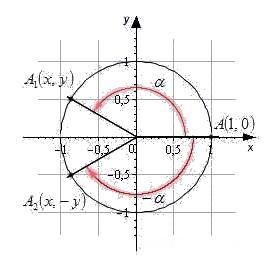
Свойства синусов, косинусов, тангенсов и котангенсов противоположных углов
Вновь обратимся к единичной окружности.
Отсюда следует свойство синусов, косинусов, тангенсов и котангенсов противоположных углов.
Свойство синусов, косинусов, тангенсов и котангенсов противоположных углов
Согласно этому свойству, справедливы равенства
Рассмотренное свойство часто используется при решении практических задач в случаях, когда нужно избавиться от отрицательных знаков углов в агрументах тригонометрических функций.